Слайд 2 Корни квадратного уравнения ах²+bx+c=0 (а≠0) можно рассматривать как абсциссы точек пересечения окружности

с центром
Q , проходящей через точку А(0;1),
и оси Ох.
Решение уравнения сводится к построению на координатной плоскости окружности с центром Q и радиусом QA (для этого и понадобятся инструменты) и определению абсцисс точек пересечения окружности с осью Ох.
Возможны 3 случая:
Слайд 31 случай
Если QA> то окружность пересекает ось Ох в двух точках М(х1 ;
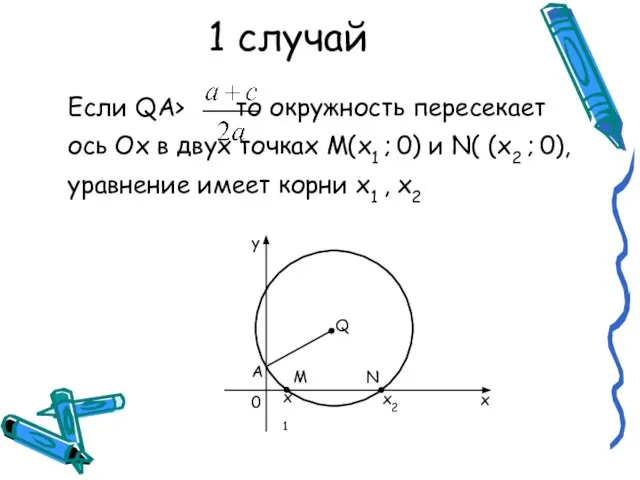
0) и N( (х2 ; 0), уравнение имеет корни х1 , х2
Слайд 42 случай
Если QA= то окружность касается оси Ох в точке М(х1 ;
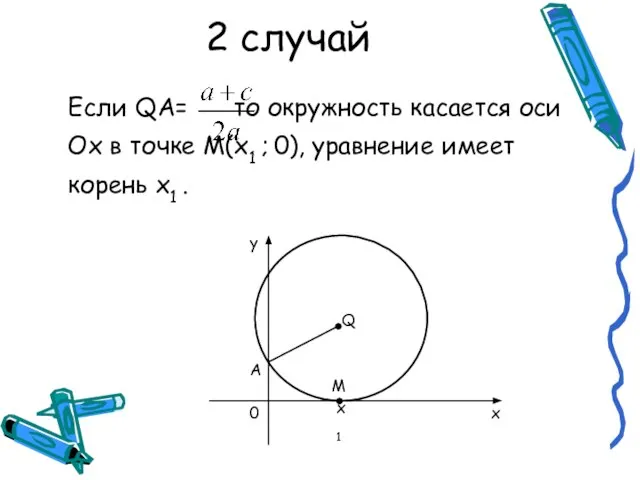
0), уравнение имеет корень х1 .
Слайд 53 случай
Если QA< то окружность не имеет общих точек с осью Ох,
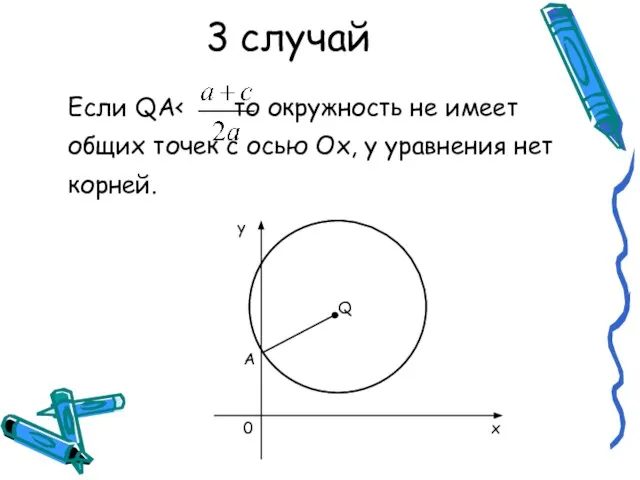
у уравнения нет корней.
Слайд 6Пример 1
Решите уравнение х²-2x+1=0.
Решение:
-в/2а=1,(а+с)/2а=1,
Q(1;1), А(0;1)
QА=1,
Окружность касается
Ох в т.М, уравнение
имеет 1

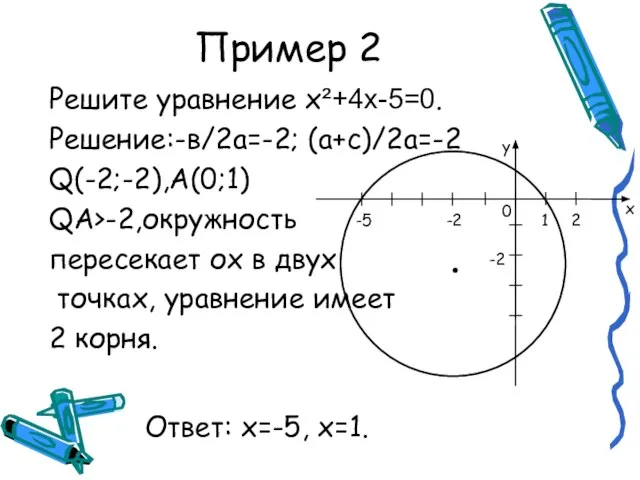
Слайд 7Пример 2
Решите уравнение х²+4x-5=0.
Решение:-в/2а=-2; (а+с)/2а=-2
Q(-2;-2),А(0;1)
QА>-2,окружность
пересекает ох в двух
точках, уравнение имеет
2
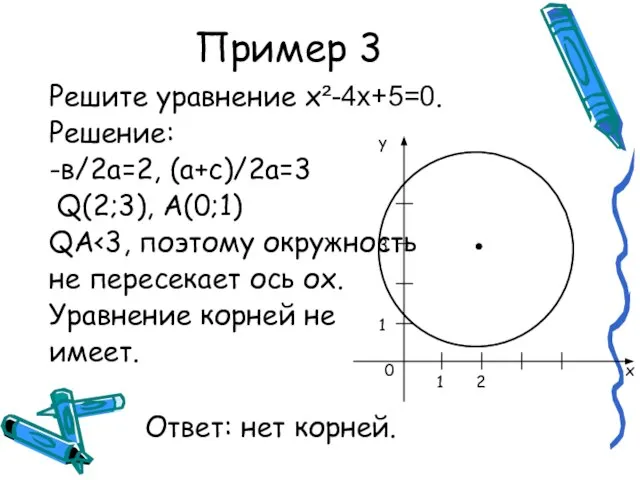
Слайд 8Пример 3
Решите уравнение х²-4x+5=0.
Решение:
-в/2а=2, (а+с)/2а=3
Q(2;3), А(0;1)
QА<3, поэтому окружность
не пересекает ось ох.
Уравнение
корней не
имеет.
Ответ: нет корней.
Слайд 9Замечание
Конечно, решать уравнения по формуле проще, чем выполнять построения. Но нам сейчас

интересно отметить важный факт: квадратные уравнения могут быть решены с привлечением геометрии. Правда, этот способ не позволяет получать точные решения в случае произвольных коэффициентов уравнения.








 Потребность ? ДОЛГОВЕЧНОСТЬ
Потребность ? ДОЛГОВЕЧНОСТЬ Обзор рынка электронной торговли в России и в мире
Обзор рынка электронной торговли в России и в мире Написание слов со звонкими и глухими, мягкими и твёрдыми согласными Перенос слов
Написание слов со звонкими и глухими, мягкими и твёрдыми согласными Перенос слов Презентация на тему: Процент. Три задачи на проценты.
Презентация на тему: Процент. Три задачи на проценты. Материалы, методы и приемы, используемые в решениях задач по черчению
Материалы, методы и приемы, используемые в решениях задач по черчению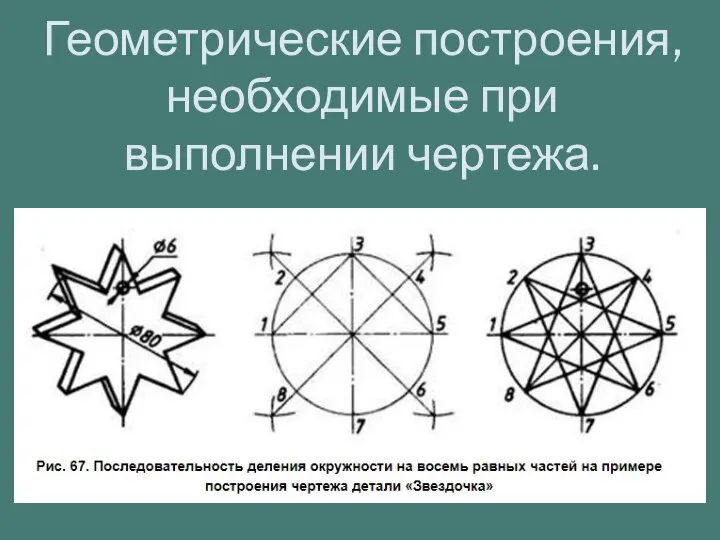 Геометрические построения, необходимые при выполнении чертежа
Геометрические построения, необходимые при выполнении чертежа В рыцарском замке
В рыцарском замке Программа развития муниципального автономного образовательного учреждения «Межшкольный учебный комбинат города Ишима» (МА ОУ
Программа развития муниципального автономного образовательного учреждения «Межшкольный учебный комбинат города Ишима» (МА ОУ  Закон Божий Ветхий Завет
Закон Божий Ветхий Завет Изонить. Фигуры и схемы
Изонить. Фигуры и схемы Презентация на тему Дворцовые перевороты
Презентация на тему Дворцовые перевороты  Пространственные виды искусства
Пространственные виды искусства Москитные полотно
Москитные полотно Презентация на тему Порядок выполнения действий (5 класс)
Презентация на тему Порядок выполнения действий (5 класс) Портрет идеального кандидата по PR
Портрет идеального кандидата по PR Отношения между понятиями
Отношения между понятиями Блюда и гарниры из овощей и грибов
Блюда и гарниры из овощей и грибов Основные направления деятельности студенческих отрядов
Основные направления деятельности студенческих отрядов Азбука поучительных историй о пешеходах и пассажирах
Азбука поучительных историй о пешеходах и пассажирах Игровые блоки по уголовному процессу
Игровые блоки по уголовному процессу Как человек познаёт мир и самого себя
Как человек познаёт мир и самого себя Народы Северного Кавказа. Аварцы
Народы Северного Кавказа. Аварцы Market Analysis for Shopping Centers Demand, Supply
Market Analysis for Shopping Centers Demand, Supply Презентация на тему Денежная система
Презентация на тему Денежная система  Продукция Phenomenex в методических решениях компании «Аквилон»
Продукция Phenomenex в методических решениях компании «Аквилон» Психологическая защита. Почему сопротивление клиента благо для психолога?
Психологическая защита. Почему сопротивление клиента благо для психолога? 10 Нейминговых решений
10 Нейминговых решений Религия как одна из форм культуры
Религия как одна из форм культуры