Содержание
- 2. «Но когда эти науки (алгебра и геометрия) объединились, они энергично поддержали друг друга и быстро зашагали
- 3. АКТУАЛЬНОСТЬ РАБОТЫ определяется включением подобных задач в ЕГЭ. ПРОБЛЕМА ИССЛЕДОВАНИЯ: возможность применения координатного метода при решении
- 4. «МЕТОД ОБЛАСТЕЙ» один из частных случаев координатного метода. Идея «МЕТОДА ОБЛАСТЕЙ» заключается в том, что решение
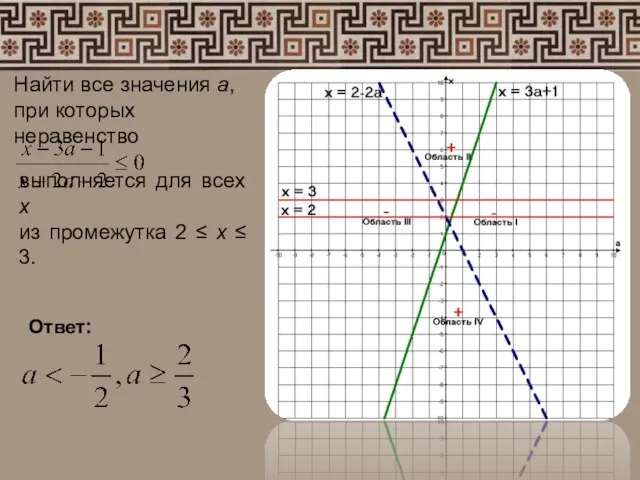
- 5. Найти все значения а, при которых неравенство выполняется для всех х из промежутка 2 ≤ х
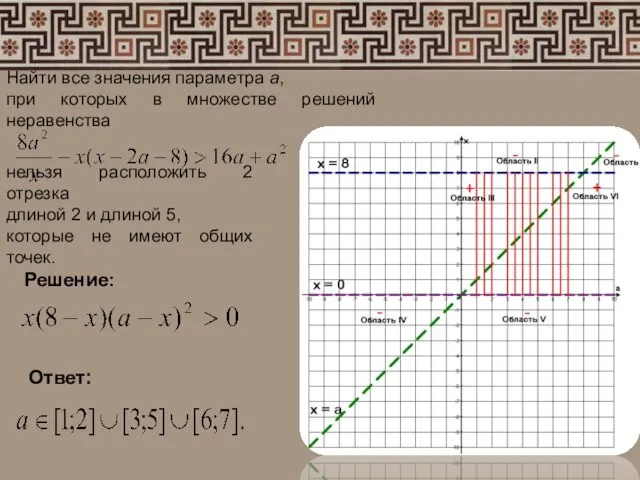
- 6. Найти все значения параметра а, при которых в множестве решений неравенства нельзя расположить 2 отрезка длиной
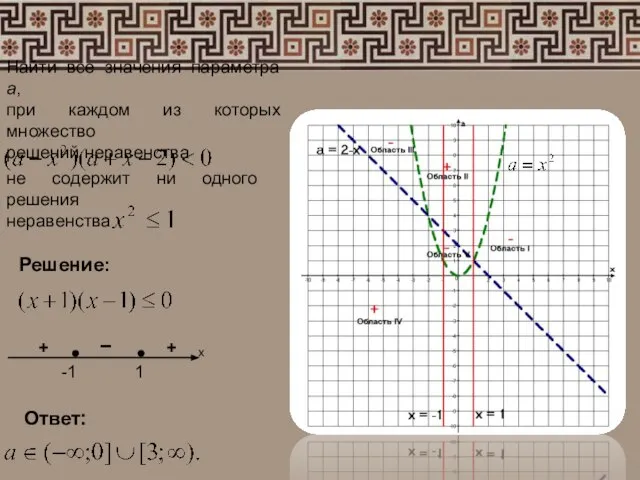
- 7. Найти все значения параметра а, при каждом из которых множество решений неравенства не содержит ни одного
- 8. Найти все значения параметра а, при которых множество решений неравенства содержит все неотрицательные решения неравенства Решение:
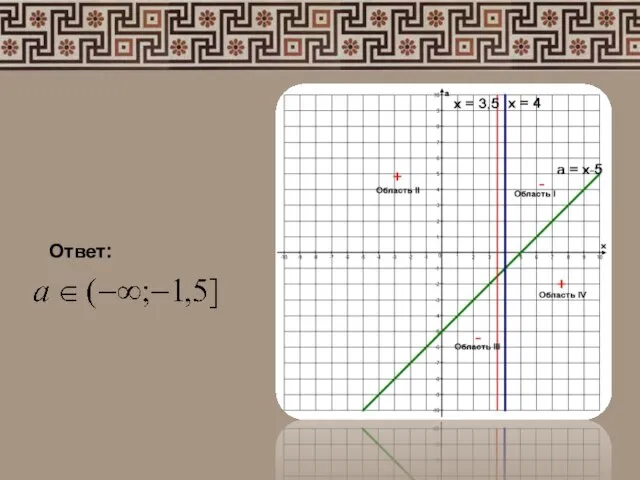
- 9. Ответ:
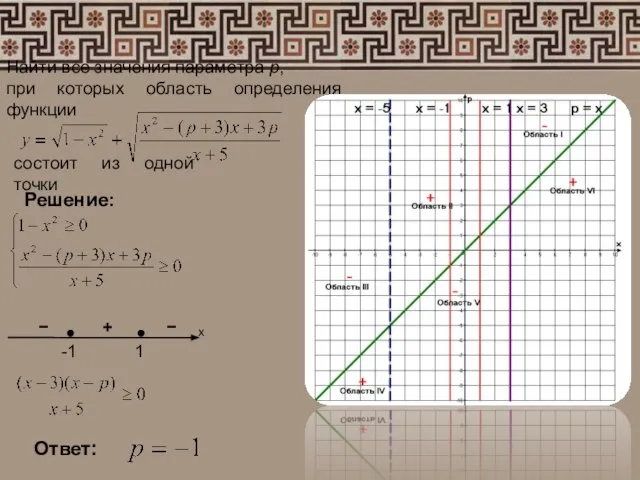
- 10. Найти все значения параметра р, при которых область определения функции состоит из одной точки Решение: Ответ:
- 11. Таким образом, при решении неравенств «методом областей» необходимо: разложить данное неравенство на множители; найти и построить
- 13. Скачать презентацию




 Андрей Тарковский, фильм Зеркало (кадры из фильма)
Андрей Тарковский, фильм Зеркало (кадры из фильма) Движение декабристов – восстание или мирная форма протеста, демонстрация?
Движение декабристов – восстание или мирная форма протеста, демонстрация? Инвалидность. Понятие
Инвалидность. Понятие 20141109_test_10_klass
20141109_test_10_klass Питание и органы пищеварения 4. Выполните 3 задания, записывая результат на листочке. 1.Введите своё имя. 2. Выберите режим «Без подск
Питание и органы пищеварения 4. Выполните 3 задания, записывая результат на листочке. 1.Введите своё имя. 2. Выберите режим «Без подск Потребности и реклама
Потребности и реклама СПИД и его профилактика
СПИД и его профилактика  ЗемледельцыАттики
ЗемледельцыАттики Презентация на тему Закон Кулона
Презентация на тему Закон Кулона Социальная и духовная болезнь
Социальная и духовная болезнь 20170212_hramy_18_veka_smolenskoy_oblasti
20170212_hramy_18_veka_smolenskoy_oblasti Презентация по физике:Механические волны
Презентация по физике:Механические волны Функции и их графики. Способы задания функции
Функции и их графики. Способы задания функции Всероссийский форум: Потребительская кооперация – открытые возможности для каждого на благо всех
Всероссийский форум: Потребительская кооперация – открытые возможности для каждого на благо всех Петр Павлович Ершов
Петр Павлович Ершов Учет риска при оценке эффективности инвестиционных проектов
Учет риска при оценке эффективности инвестиционных проектов Японские Хокку
Японские Хокку 3 причины, почему нужно делать интерактивные проекты уже в этом году
3 причины, почему нужно делать интерактивные проекты уже в этом году «ПОЖАРНАЯ БЕЗОПАСНОСТЬ»НиколаеваНадежда Ивановна
«ПОЖАРНАЯ БЕЗОПАСНОСТЬ»НиколаеваНадежда Ивановна Презентация на тему Рекомендации по написанию исследовательских работ
Презентация на тему Рекомендации по написанию исследовательских работ Деньги. Презентация Школы богатого фрилансера
Деньги. Презентация Школы богатого фрилансера Креатив и потребности ЦА. Структура мотивации потребителей
Креатив и потребности ЦА. Структура мотивации потребителей Тема: «Методика разработки подсистемы конфигурирования системы ЧПУ»
Тема: «Методика разработки подсистемы конфигурирования системы ЧПУ» Золотые медалисты нашей школы
Золотые медалисты нашей школы Образно-тематическая инсталляция
Образно-тематическая инсталляция Презентация на тему В.Г.Распутин
Презентация на тему В.Г.Распутин Об’єкти оподаткування та операції, що не є об’єктом оподаткування
Об’єкти оподаткування та операції, що не є об’єктом оподаткування Реконструкция ул. Бударина и Набережной Оми Напастюк
Реконструкция ул. Бударина и Набережной Оми Напастюк