Решение неравенств второй степени с одной переменной

Повторим квадратичную функцию
Дайте определение квадратичной функции.
Что представляет собой график квадратичной функции?
Как построить график квадратичной функции?

Определить направление ветвей параболы;
Найти координаты вершины параболы (m; n);
Построить вершину параболы в координатной плоскости;
Определить ось симметрии (x = m);
Найти дополнительные точки принадлежащие параболе;
Построить точки в координатной плоскости с учетом симметрии параболы.

Какие точки необходимо выбрать для более точного построения параболы?

Как найти точки пересечения квадратичной функции с ось Х?
Как найти точки пересечения квадратичной функции с осью У?

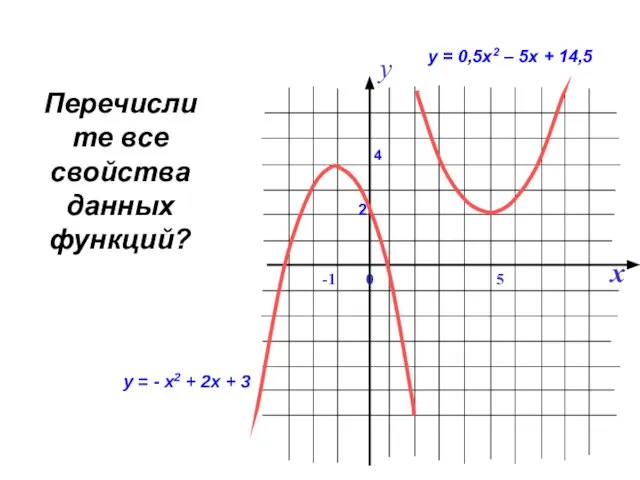
Перечислите все свойства данных функций?
2
4
у = 0,5х2 – 5х + 14,5
у = - х2 + 2х + 3

Решение неравенств второй степени с одной переменной
Неравенства вида ах2 + bx + c > 0 и ах2 + bx + c < 0, где а, b и с – некоторые числа, причем а ≠ 0, неравенства второй степени с одной переменной.

Решение неравенств второй степени с одной переменной можно рассматривать как нахождение промежутков, в которых соответствующая квадратичная функция принимает положительные или отрицательные значения.

Что необходимо знать для определения промежутков, в которых соответствующая квадратичная функция принимает положительные или отрицательные значения?

Направление ветвей параболы.
Нахождение общих точек графика с осью абсцисс.

Решим неравенство 5х2 + 9х – 2 < 0
Рассмотрим функцию у = 5х2 + 9х – 2
Графиком этой функции является парабола, ветви которой направлены вверх.
Выясним, как расположена парабола относительно оси х. Для этого решим уравнение 5х2 + 9х – 2 = 0.
5х2 + 9х – 2 = 0.
D = b2 – 4ac = 92 - 4⋅5⋅(-2) = 81 + 40 = =121,

Значит , парабола пересекает ось х в двух точках, абсциссы которых равны – 2 и

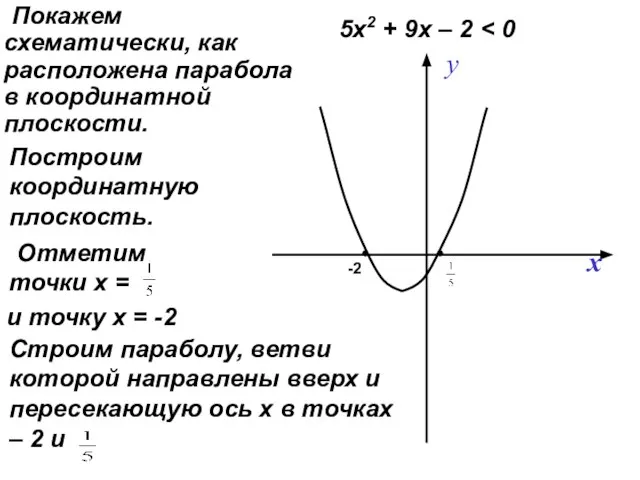
Покажем схематически, как расположена парабола в координатной плоскости.
-2
Построим координатную плоскость.
и точку х = -2
Строим параболу, ветви которой направлены вверх и пересекающую ось х в точках – 2 и
5х2 + 9х – 2 < 0

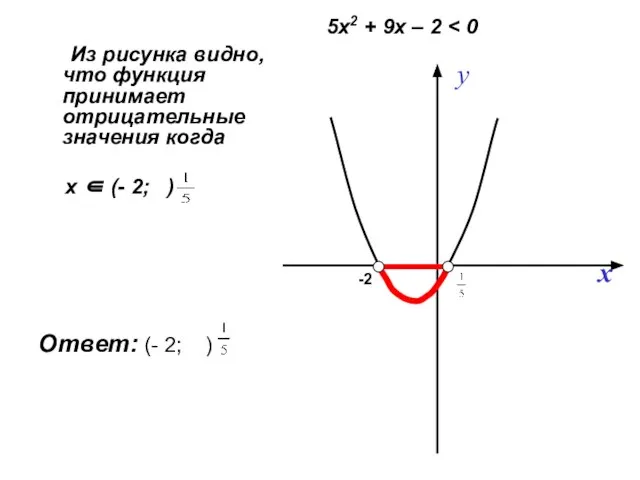
Из рисунка видно, что функция принимает отрицательные значения когда
-2
х ∈ (- 2; )
Ответ: (- 2; )
5х2 + 9х – 2 < 0

Решим неравенство: -2х2 + 7х < 0
Рассмотрим функцию у = -2х2 + 7х
Графиком этой функции является парабола, ветви которой направлены вниз.
Выясним, как расположена парабола относительно оси х.
Решим уравнение - 2х2 + 7х = 0.
- 2х2 + 7х = 0.
-2х(х – 3,5)= 0,
х = 0 или х = 3,5.
Значит , парабола пересекает ось х в двух точках, абсциссы которых равны 0 и 3,5.

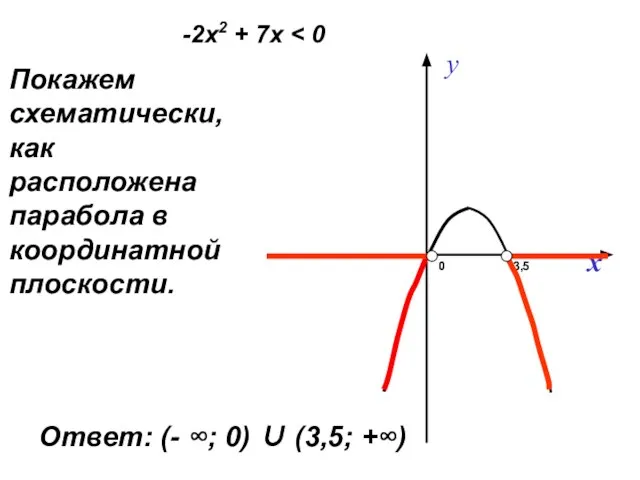
Покажем схематически, как расположена парабола в координатной плоскости.
0
3,5
-2х2 + 7х < 0
Ответ: (- ∞; 0) ∪ (3,5; +∞)

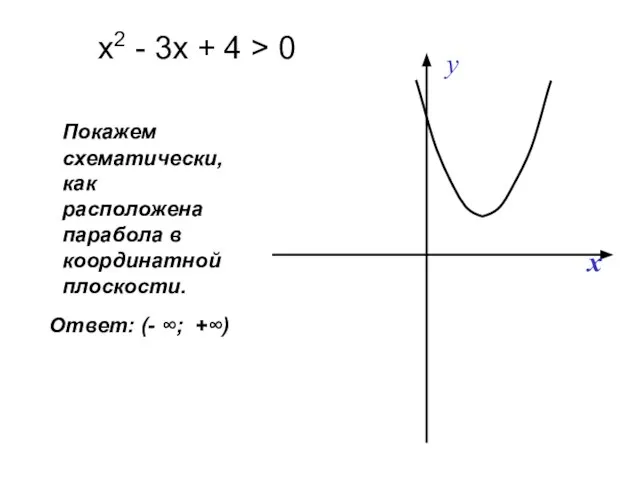
Решим неравенство: х2 - 3х + 4 > 0
Рассмотрим функцию у = х2 - 3х + 4.
Графиком этой функции является парабола, ветви которой направлены вверх.
Выясним, как расположена парабола относительно оси х.
Решим уравнение х2 - 3х + 4 = 0.
х2 - 3х + 4 = 0.
D = b2 – 4ac = (- 3)2 - 4⋅1⋅ 4 = 9 - 16 = - 7,
D < 0, уравнение не имеет корней.
Значит , парабола ….

Покажем схематически, как расположена парабола в координатной плоскости.
х2 - 3х + 4 > 0
Ответ: (- ∞; +∞)

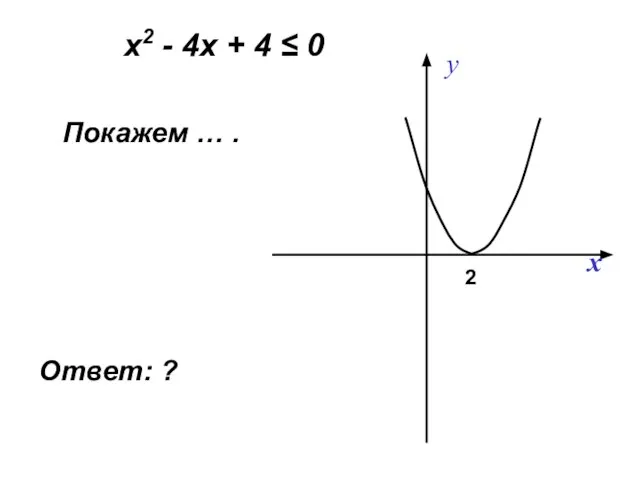
Решим неравенство: х2 - 4х + 4 ≤ 0
Рассмотрим функцию …
Графиком этой функции является …, ветви которой направлены ….
Выясним, как расположена парабола относительно оси х. Для этого решим уравнение … .

х2 - 4х + 4 = 0.
D = b2 – 4ac = (- 4)2 - 4⋅1⋅ 4 = 16 - 16 = 0,
D < 0, уравнение 1 имеет корень.
х = …
Значит , парабола ….

х2 - 4х + 4 ≤ 0
Покажем … .
2
Ответ: ?

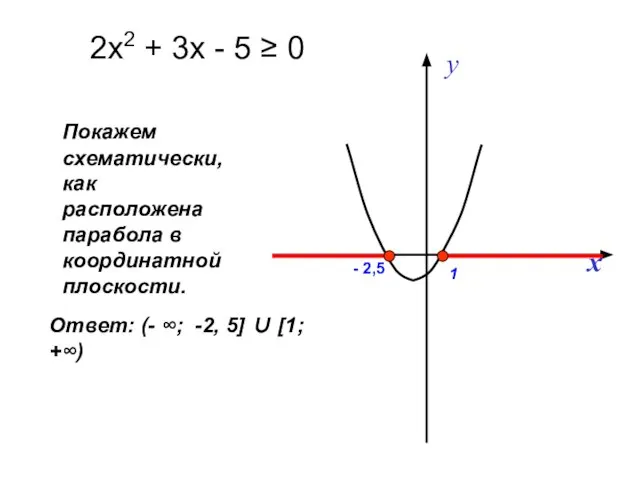
Решите неравенство:
2х2 + 3х – 5 ≥ 0
Рассмотрим функцию у = 2х2 + 3х - 5.
Графиком ...
Выясним, ...
Решим уравнение: 2х2 + 3х - 5 = 0.
2х2 + 3х - 5 = 0.
D = b2 – 4ac = 32 - 4⋅2⋅ (-5) = 9 + 40 =
= 49,
D > 0, уравнение имеет 2 корня. …
Значит , парабола ….

Покажем схематически, как расположена парабола в координатной плоскости.
2х2 + 3х - 5 ≥ 0
Ответ: (- ∞; -2, 5] ∪ [1; +∞)
1
- 2,5

Как решить квадратное неравенство
ах2 + bx + c > (<)?
Рассмотреть функцию
у = ах2 + bx + c.
Определить направление ветвей параболы.
Найти корни квадратного трехчлена.
Отметить корни на оси х и через отмеченные точки провести схематически параболу.

Отметить корни на оси х и через отмеченные точки провести схематически параболу.
Если а > 0, то ветви параболы направлены вверх.
Если а < 0, то ветви параболы направлены вниз.

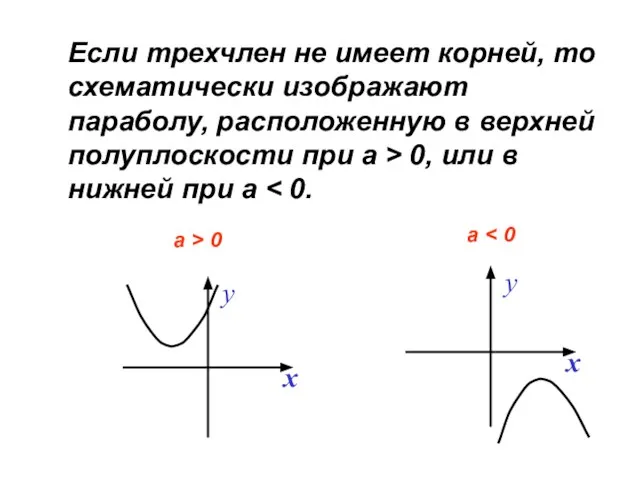
Если трехчлен не имеет корней, то схематически изображают параболу, расположенную в верхней полуплоскости при а > 0, или в нижней при а < 0.
а > 0
а < 0

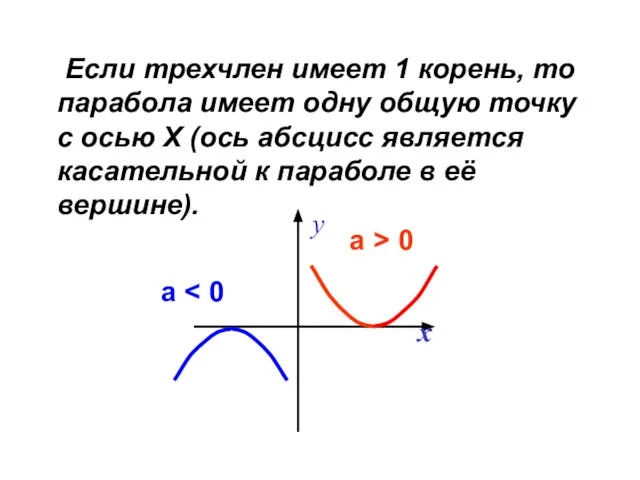
Если трехчлен имеет 1 корень, то парабола имеет одну общую точку с осью Х (ось абсцисс является касательной к параболе в её вершине).

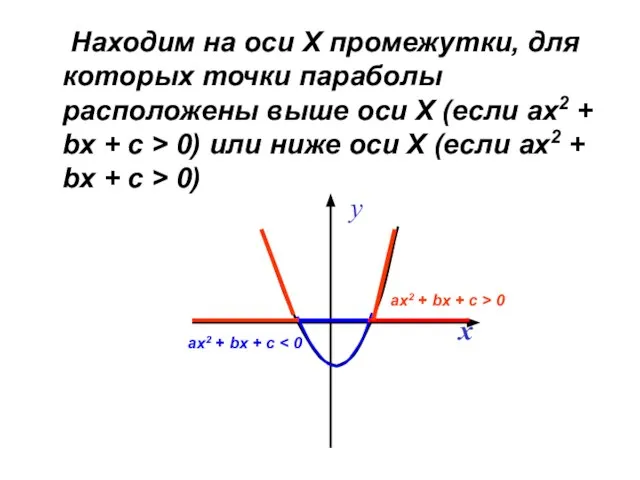
Находим на оси Х промежутки, для которых точки параболы расположены выше оси Х (если ах2 + bx + c > 0) или ниже оси Х (если ах2 + bx + c > 0)

Решите самостоятельно
x2 – 16 ≤ 0;
-7х2 – 10х – 7 > 0.

Проверка
x2 – 16 ≤ 0
- 4
4
Ответ: [ - 4; 4]

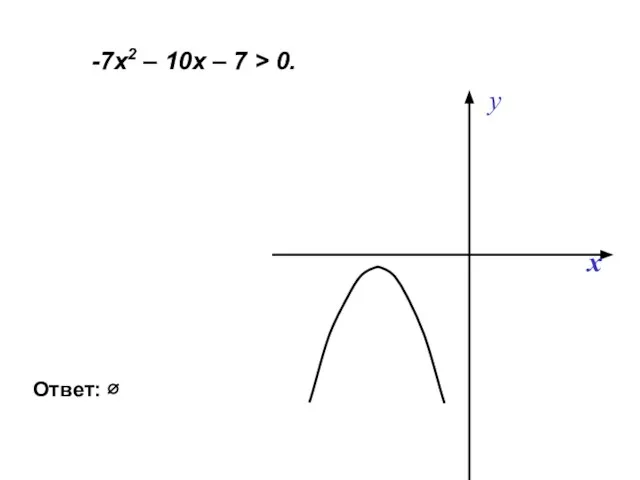
-7х2 – 10х – 7 > 0.
Ответ: ∅

Домашнее задание
п. 8 № 116. (№ 122 по желанию)