Содержание
- 2. Задачи Теория и практика №1 №2 №3 №4 №5 №6
- 3. Теория Теорема. Медиана делит треугольник на два равновеликих треугольника. Теорема. Медиана прямоугольного треугольника, проведенная из вершины
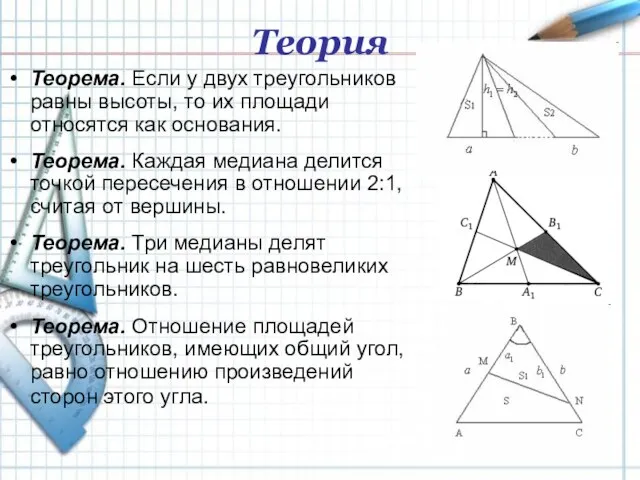
- 4. Теория Теорема. Если у двух треугольников равны высоты, то их площади относятся как основания. Теорема. Каждая
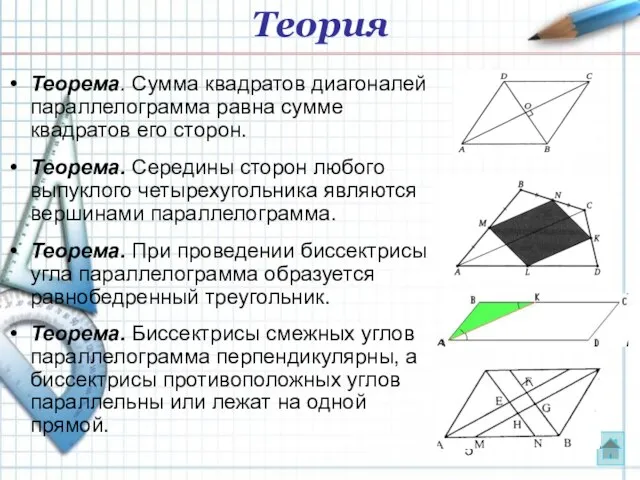
- 5. Теорема. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Теорема. Середины сторон любого выпуклого четырехугольника
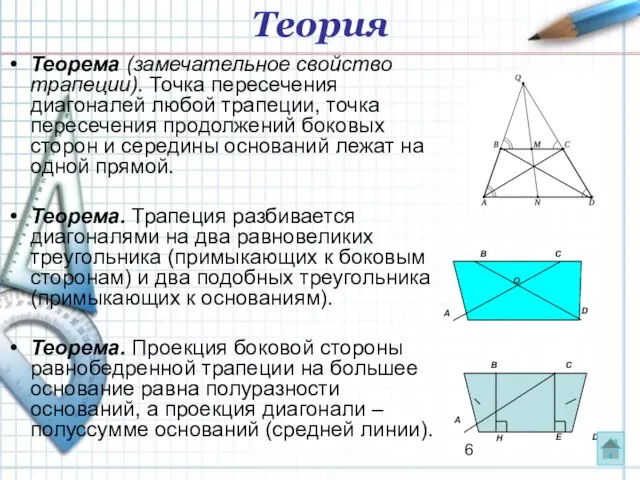
- 6. Теорема (замечательное свойство трапеции). Точка пересечения диагоналей любой трапеции, точка пересечения продолжений боковых сторон и середины
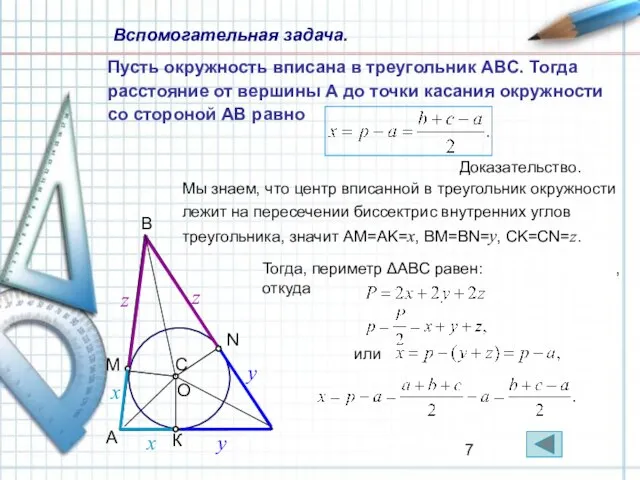
- 7. Пусть окружность вписана в треугольник ABC. Тогда расстояние от вершины A до точки касания окружности со
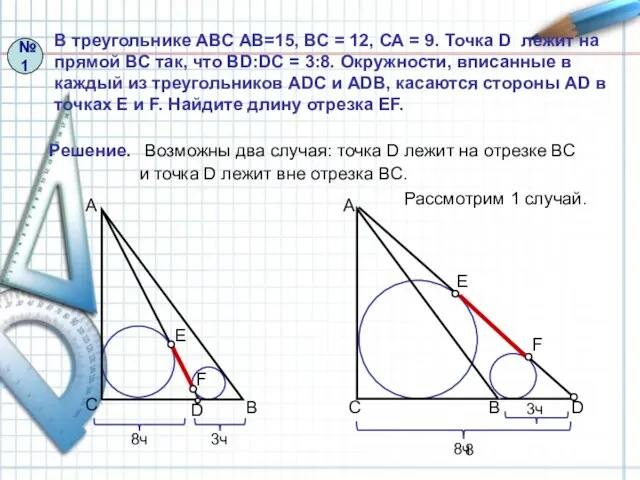
- 8. В треугольнике АВС АВ=15, ВС = 12, СА = 9. Точка D лежит на прямой ВС
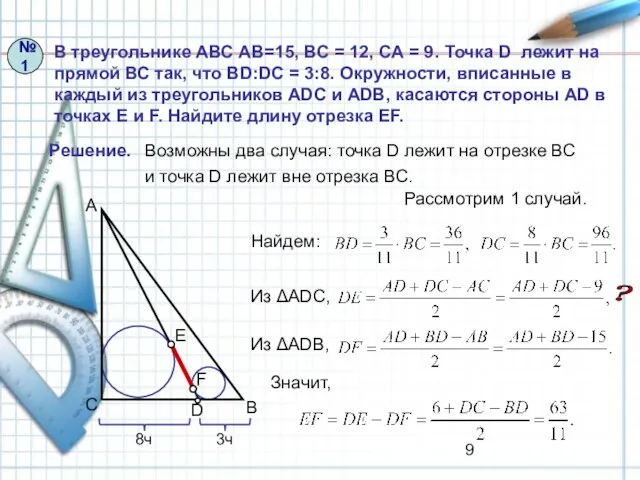
- 9. В треугольнике АВС АВ=15, ВС = 12, СА = 9. Точка D лежит на прямой ВС
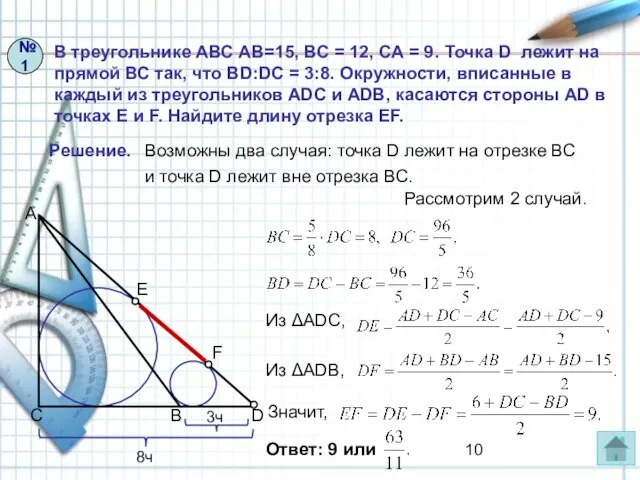
- 10. В треугольнике АВС АВ=15, ВС = 12, СА = 9. Точка D лежит на прямой ВС
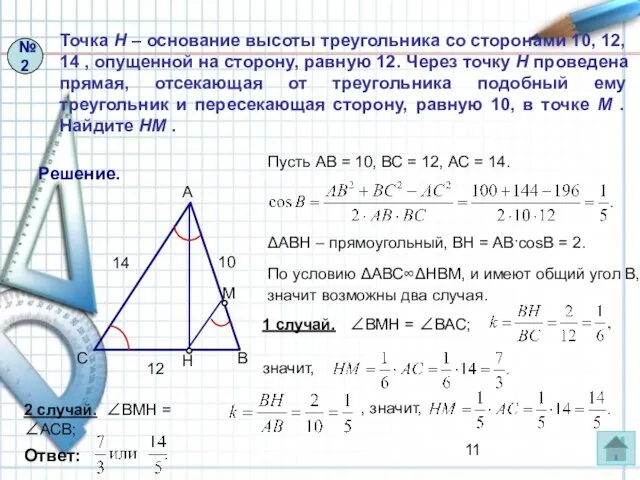
- 11. Точка H – основание высоты треугольника со сторонами 10, 12, 14 , опущенной на сторону, равную
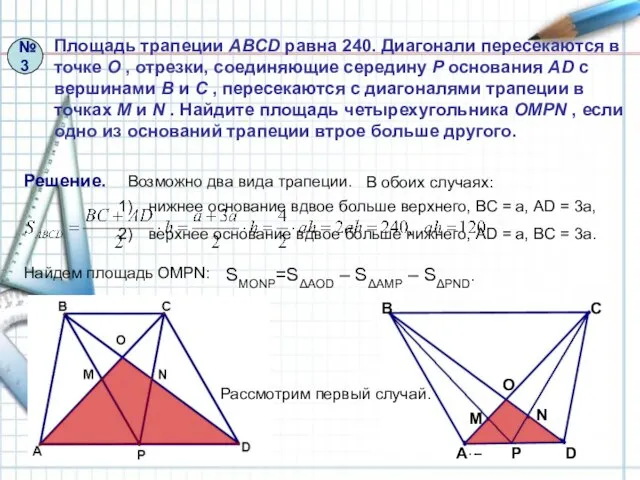
- 12. нижнее основание вдвое больше верхнего, BC = a, АD = 3a, верхнее основание вдвое больше нижнего,
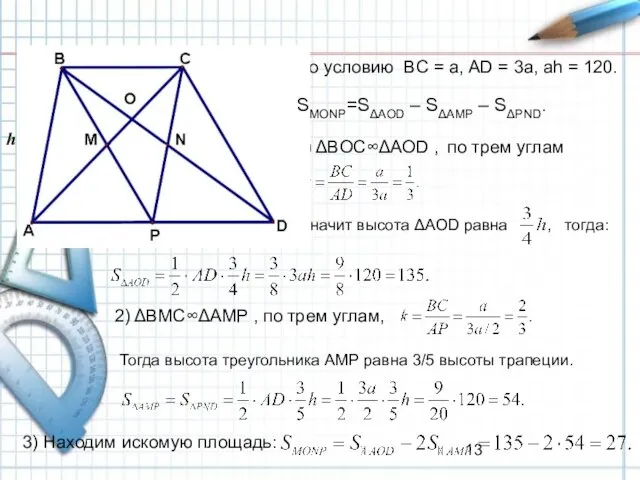
- 13. По условию BC = a, АD = 3a, аh = 120. 1) ΔBOC∞ΔAOD , по трем
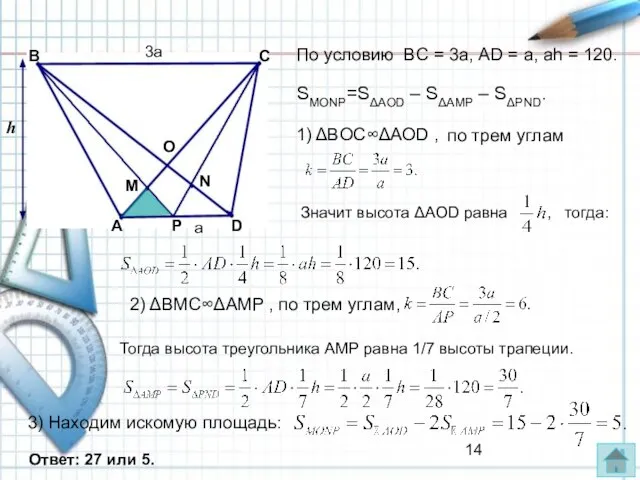
- 14. По условию BC = 3a, АD = a, аh = 120. 1) ΔBOC∞ΔAOD , по трем
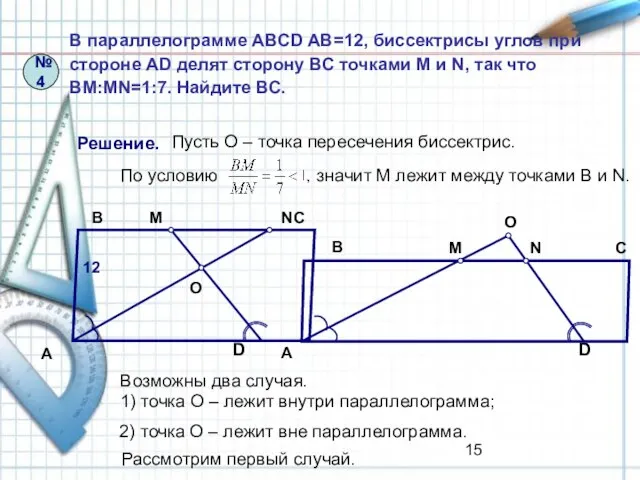
- 15. №4 В параллелограмме ABCD AB=12, биссектрисы углов при стороне AD делят сторону ВС точками M и
- 16. №4 В параллелограмме ABCD AB=12, биссектрисы углов при стороне AD делят сторону ВС точками M и
- 17. №4 В параллелограмме ABCD AB=12, биссектрисы углов при стороне AD делят сторону ВС точками M и
- 18. Сторона ромба ABCD равна 4√7, а косинус угла А равен 0,75. Высота BH пересекает диагональ AC
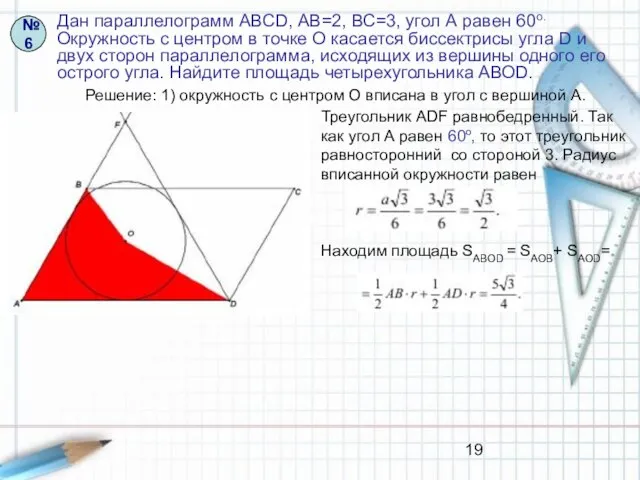
- 19. Дан параллелограмм АВСD, АВ=2, ВС=3, угол А равен 60о. Окружность с центром в точке О касается
- 20. Дан параллелограмм АВСD, АВ=2, ВС=3, угол А равен 60о. Окружность с центром в точке О касается
- 22. Скачать презентацию






 Группа «Минимизация рисков перехода на ФГОС НОО. Мониторинг ФГОС НОО»
Группа «Минимизация рисков перехода на ФГОС НОО. Мониторинг ФГОС НОО» Everyday slang. Сленг на каждый день
Everyday slang. Сленг на каждый день Степень сравнения прилагательных
Степень сравнения прилагательных Открытки с 9 мая
Открытки с 9 мая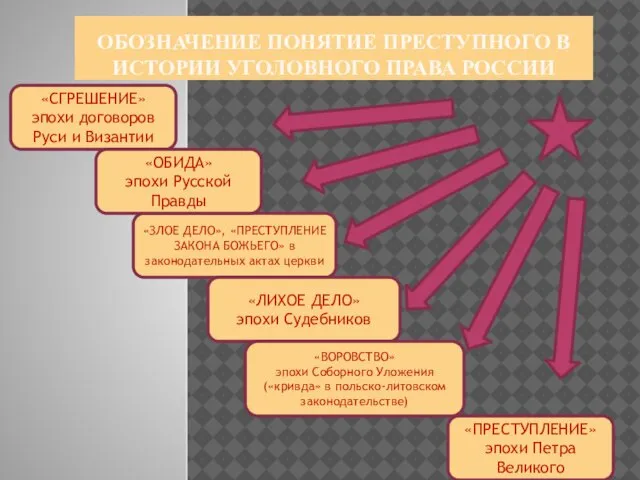 Понятие преступления и формы его множественности. Тема 3
Понятие преступления и формы его множественности. Тема 3 Разработка Учебных планов бакалавров и магистров по направлению «Энергетическое машиностроение» профиль подготовки бакалавров:
Разработка Учебных планов бакалавров и магистров по направлению «Энергетическое машиностроение» профиль подготовки бакалавров:  СТРУКТУРА РОССИЙСКОГО АВТОПАРКАГРУЗОВЫХ АВТОМОБИЛЕЙ ИАК «ВладВнешСервис», январь 2010
СТРУКТУРА РОССИЙСКОГО АВТОПАРКАГРУЗОВЫХ АВТОМОБИЛЕЙ ИАК «ВладВнешСервис», январь 2010 Прокачай в себе волонтера
Прокачай в себе волонтера praktika_po_zhkkh
praktika_po_zhkkh «Информационно-коммуникационные технологии в деятельности учителя математики»(18 часов)
«Информационно-коммуникационные технологии в деятельности учителя математики»(18 часов) Век медный,бронзовый, железный
Век медный,бронзовый, железный Литейное производство. Прибыли и холодильники отливок. (Лекция 7)
Литейное производство. Прибыли и холодильники отливок. (Лекция 7) Олимпида 2020
Олимпида 2020 Курительные смеси
Курительные смеси Holidays
Holidays Учимся мастерству
Учимся мастерству Муниципальное общеобразовательное учреждение«Средняя общеобразовательная школа № 13 »
Муниципальное общеобразовательное учреждение«Средняя общеобразовательная школа № 13 » Управление проектных продаж
Управление проектных продаж Арт-кластер Таврида
Арт-кластер Таврида Особенности предварительного расследования уголовных дел в отношении группы лиц с участием военнослужащих
Особенности предварительного расследования уголовных дел в отношении группы лиц с участием военнослужащих Рассмотрение дел о защите прав и законных интересов группы лиц. Лекция № 17
Рассмотрение дел о защите прав и законных интересов группы лиц. Лекция № 17 «Особенности преподавания русского языка по учебному комплексу Н.Г. Гольцовой, И.В. Шамшина»
«Особенности преподавания русского языка по учебному комплексу Н.Г. Гольцовой, И.В. Шамшина» Директор ФСИН России и его полномочия
Директор ФСИН России и его полномочия ЕВРАЗ: город друзей – город идей!
ЕВРАЗ: город друзей – город идей! НИ ДНЯ БЕЗ ПРАЗДНИКА!
НИ ДНЯ БЕЗ ПРАЗДНИКА! Презентация на тему Достопримечательности Бразилии
Презентация на тему Достопримечательности Бразилии  Как найти идею
Как найти идею Тургенев биография
Тургенев биография