Содержание
- 2. Цель урока: Научиться решать системы двух линейных уравнений с двумя переменными методом алгебраического сложения.
- 3. Повторение: 1.Что называется системой двух линейных уравнений с двумя переменными? 2.Что называется решением системы?
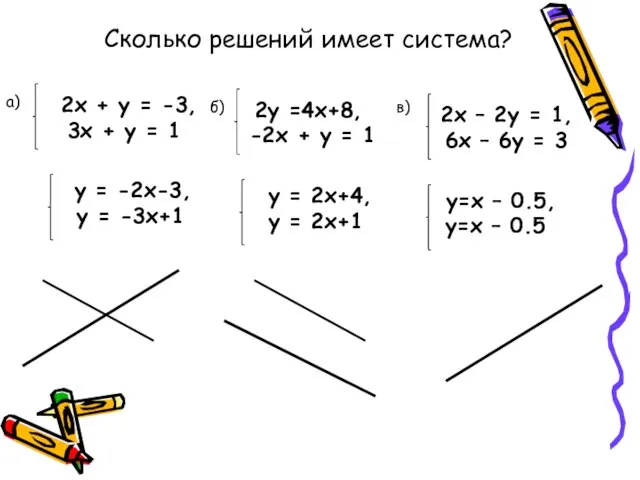
- 4. 2х + у = -3, 3х + у = 1 y = -2x-3, у = -3x+1
- 5. Задача: Четыре медвежонка тяжелее медведицы на 30 кг, а два таких же медвежонка легче медведицы на
- 6. 4y-x = 30, х -2у = 80 x = 190, у = 55 Ответ: 190 кг.
- 7. 4y-x = 30, х -2у = 80 (4y-x)+ (х -2у) = 30+80 4y-x+ х -2у =
- 8. 2х+3у=1, 5х+3у=7 Решить систему:
- 9. 2х+3у=1 ◄◄ - 5х+3у=7 (2х+3у)-(5х+3у)=1-7 2х + 3у - 5х - 3у = -6 -3х =
- 10. 4х+5у=1, 5х+7у=5 Решить систему:
- 11. 4х+5у=1, 5х+7у=5 20х+25у=5, 20х+28у=20 *5 *4 - -3у=-15, у= 5. 4х+5*5=1, 4x = -24, x =
- 12. Привести уравнения системы к одинаковым по модулю коэффициентам при переменных x и y. Если коэффициенты одинаковы,
- 13. 2х + у = -3, 3х + у = 1 Исключить одну из переменных a) 2x-y
- 14. 0 2 4 -2 -5 3 2 4 6
- 16. Скачать презентацию



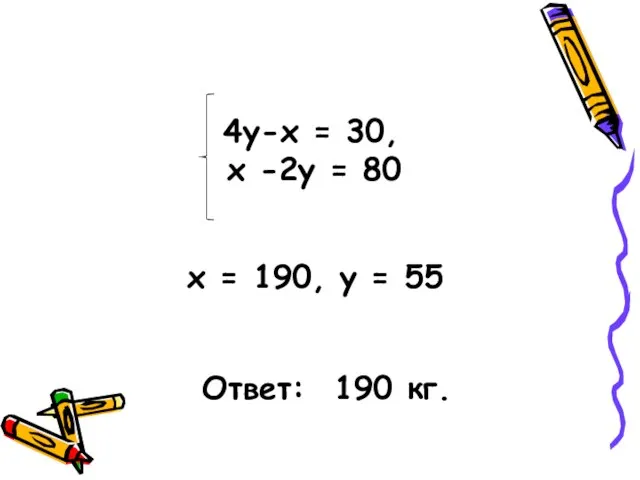
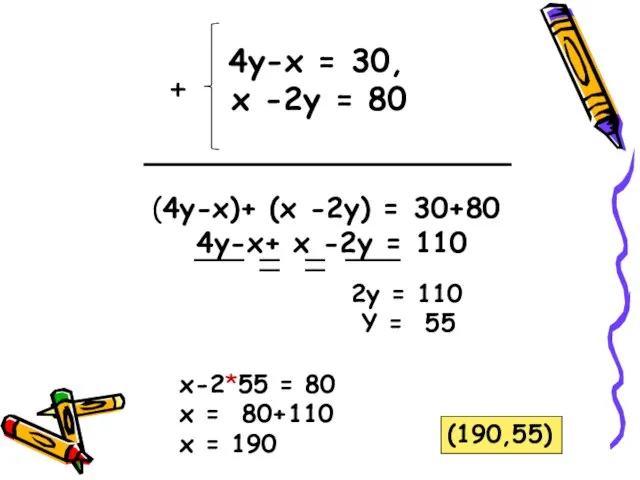
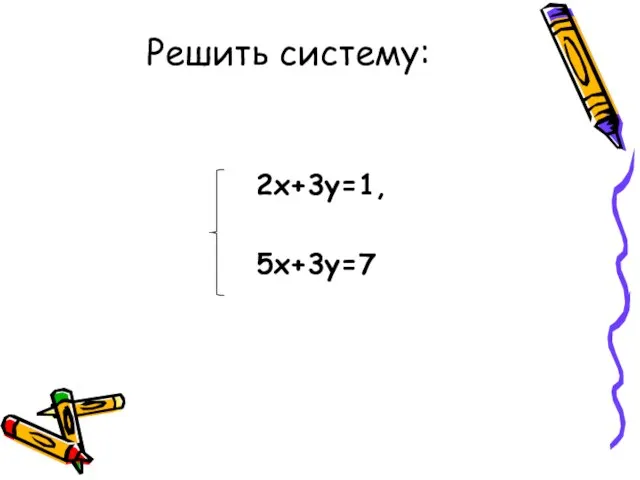
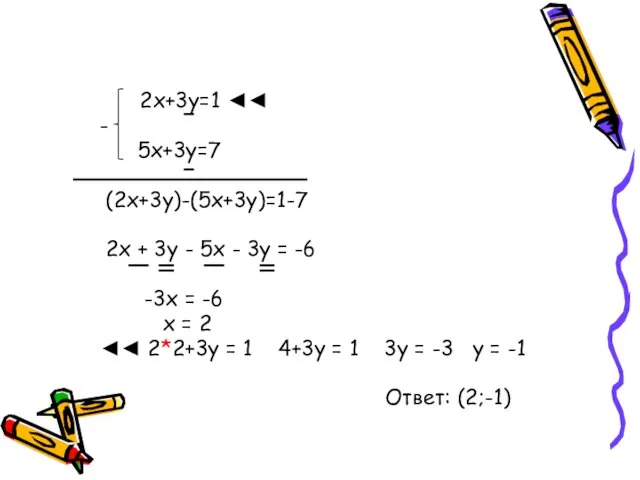
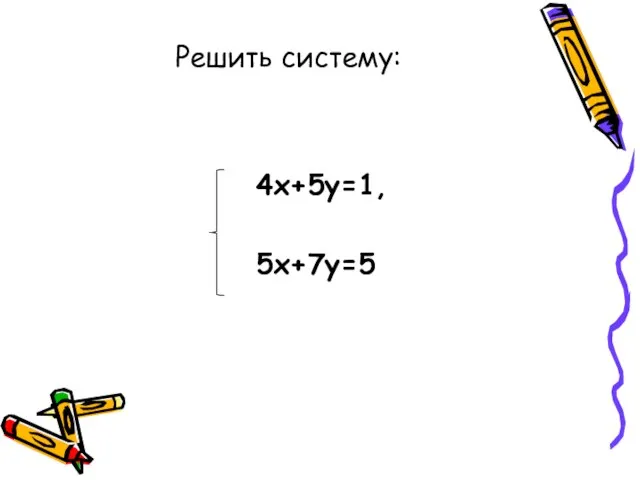
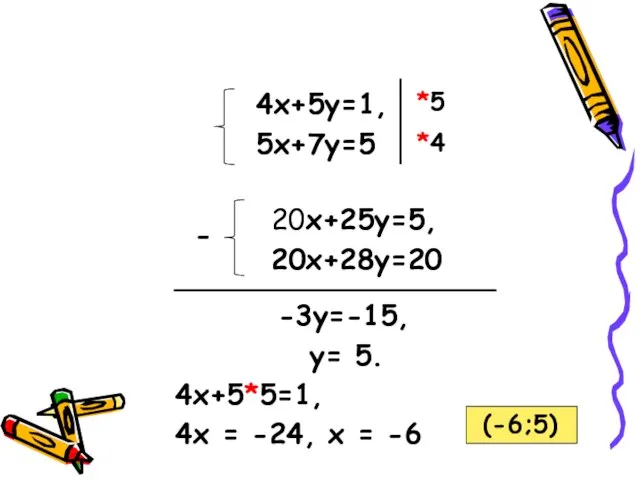

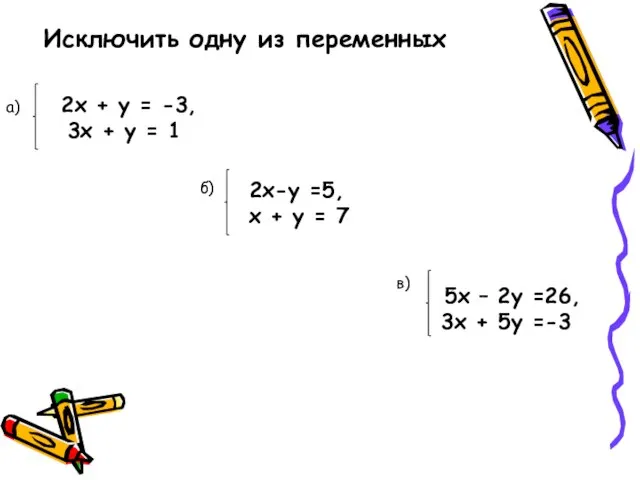
 Презентация на тему Владимир Вернадский
Презентация на тему Владимир Вернадский Презентация на тему Романтические произведения М. Горького
Презентация на тему Романтические произведения М. Горького  Дуальность природы человека
Дуальность природы человека Владимир Высоцкий
Владимир Высоцкий Кадровый консалтинг
Кадровый консалтинг КИСЛОРОД ДЕТЯМ
КИСЛОРОД ДЕТЯМ Векторы в простр
Векторы в простр Лето и дополнительное образование: новый взгляд, новое решение. Социальный проект Умные каникулы
Лето и дополнительное образование: новый взгляд, новое решение. Социальный проект Умные каникулы Тема урокаРАСТЕНИЕВОДСТВО
Тема урокаРАСТЕНИЕВОДСТВО Устройства вывода на печать
Устройства вывода на печать Выполнение задания С2.1
Выполнение задания С2.1 Типы связи слов в словосочетании
Типы связи слов в словосочетании My country legislation in the field of children health care
My country legislation in the field of children health care Взаимодействие с заинтересованными сторонами при формировании и продвижении отчета
Взаимодействие с заинтересованными сторонами при формировании и продвижении отчета Картины на дереве. Контент-стратегия Formelin.com в инстаграмм
Картины на дереве. Контент-стратегия Formelin.com в инстаграмм Работа для Вас – Rabota.ru
Работа для Вас – Rabota.ru Русской речи государь по прозванию Словарь
Русской речи государь по прозванию Словарь v Презентация на тему Административная юрисдикция
v Презентация на тему Административная юрисдикция Образовательный ресурс Исправление почерка
Образовательный ресурс Исправление почерка Афиша мероприятий Федорковского ДК на майские праздники
Афиша мероприятий Федорковского ДК на майские праздники ТРУДОУСТРОЙСТВО СТУДЕНТОВ и ВЫПУСКНИКОВ
ТРУДОУСТРОЙСТВО СТУДЕНТОВ и ВЫПУСКНИКОВ Лекция 1 (Основные понятия ФК)
Лекция 1 (Основные понятия ФК) Верховный суд США
Верховный суд США Методы подготовки к ЕГЭ
Методы подготовки к ЕГЭ Презентация на тему Касательная к окружности (8 класс)
Презентация на тему Касательная к окружности (8 класс) Производственная структура предприятия
Производственная структура предприятия 11 января самая «вежливая» дата в году отмечается Международный день «спасибо». Говорят, что "спасибо" в карман не положишь. Но с пом
11 января самая «вежливая» дата в году отмечается Международный день «спасибо». Говорят, что "спасибо" в карман не положишь. Но с пом Информационная система УНИВЕРис
Информационная система УНИВЕРис