Содержание
- 2. Содержание. Вводная часть, повторение теоретического материала. Решение тригонометрических уравнений. Проблемы, возникающие при решении тригонометрических уравнений.
- 3. ЦЕЛЬ: Повторить решение тригонометрических уравнений. 1. Знать формулы для решения простейших тригонометрических уравнений. 2. Различать типы
- 4. Устная работа. Решите уравнения А) 3 х – 5 = 7 Б) х2 – 8 х
- 5. Устная работа Упростите выражения А) (sin a – 1) (sin a + 1) Б) sin2 a
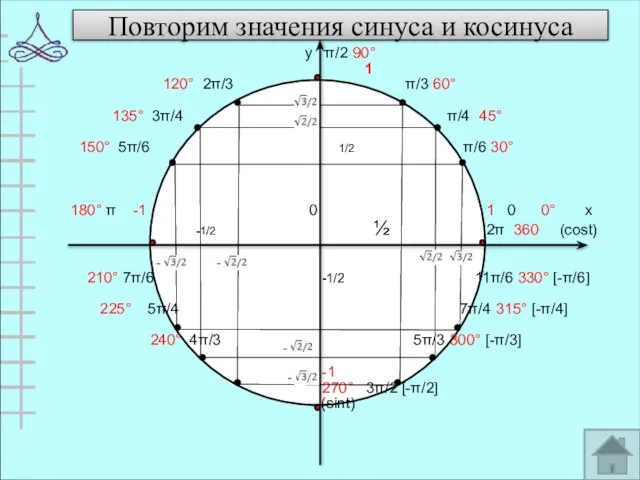
- 6. Повторим значения синуса и косинуса у π/2 90° 1 120° 2π/3 π/3 60° 135° 3π/4 π/4
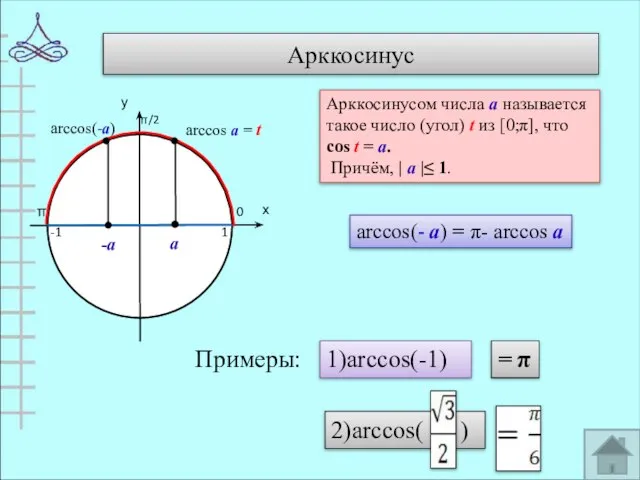
- 7. Арккосинус 0 π 1 -1 arccos(-а) Арккосинусом числа а называется такое число (угол) t из [0;π],
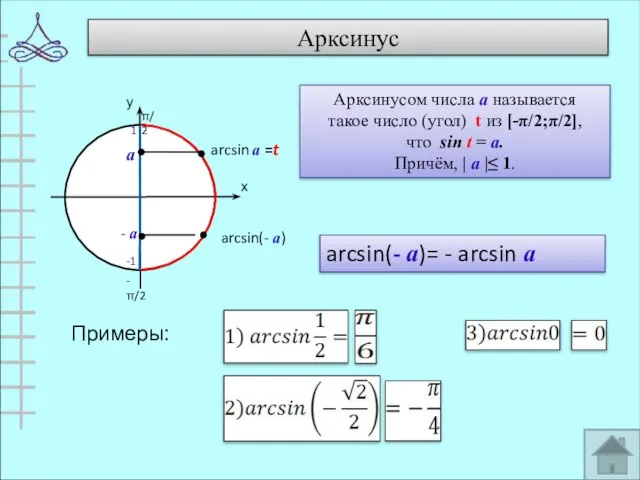
- 8. Арксинус Примеры: а - а arcsin(- а)= - arcsin а Арксинусом числа а называется такое число
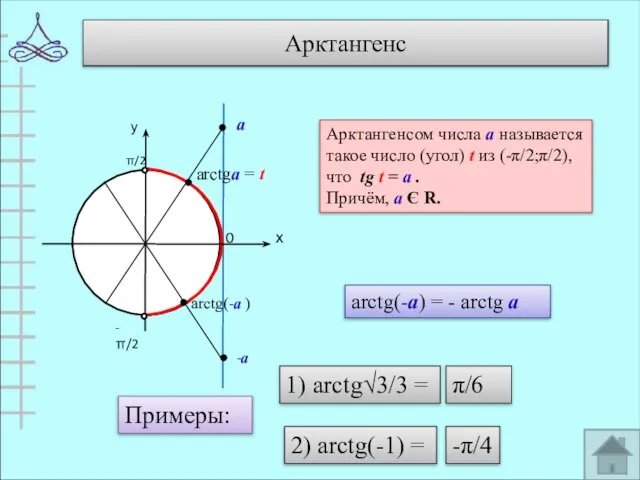
- 9. Арктангенс 0 arctgа = t Арктангенсом числа а называется такое число (угол) t из (-π/2;π/2), что
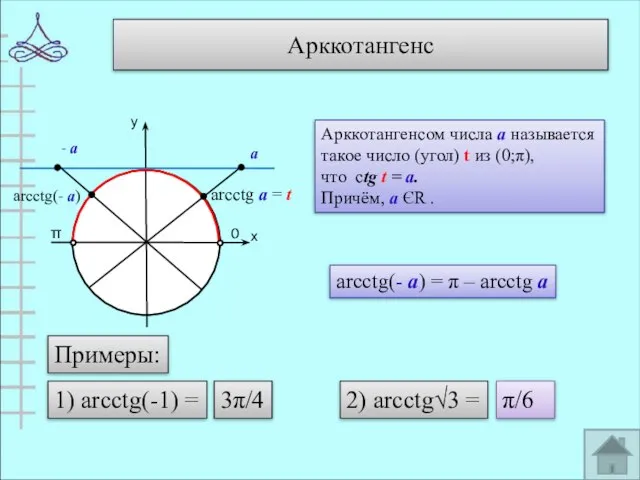
- 10. Арккотангенс у х 0 π arcctg а = t Арккотангенсом числа а называется такое число (угол)
- 11. Повторение 1 вариант sin (-π/3) cos 2π/3 tg π/6 ctg π/4 cos (-π/6) sin 3π/4 arcsin
- 12. Повторение Ответы 1 вариант - √3/2 - 1/2 √3/3 1 √3/2 √2/2 π/4 0 - π/6
- 13. Формулы корней простейших тригонометрических уравнений 1.cost = а , где |а| ≤ 1 или Частные случаи
- 14. Формулы корней простейших тригонометрических уравнений 2. sint = а, где | а |≤ 1 или Частные
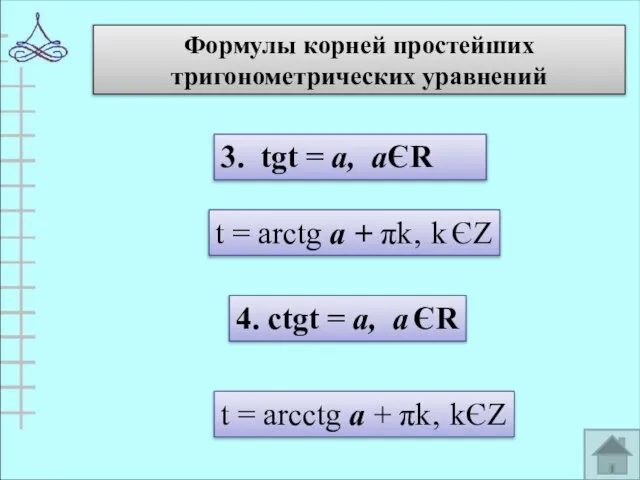
- 15. Формулы корней простейших тригонометрических уравнений 3. tgt = а, аЄR t = arctg а + πk‚
- 16. При каких значениях х имеет смысл выражение: 1.arcsin(2x+1) 2.arccos(5-2x) 3.arccos(x²-1) 4.arcsin(4x²-3x) 1) -1≤ 2х+1 ≤1 -2≤
- 17. Примеры: cost= - ; 2) sint = 0; 3) tgt = 1; t= ±arccos(-1/2)+2πk, kЄZ t=
- 18. Решение простейших уравнений tg2x = -1 2x = arctg (-1) + πk, kЄZ 2x = -π/4
- 19. Виды тригонометрических уравнений 1.Сводимые к квадратным Решаются методом введения новой переменной a∙sin²x + b∙sinx + c=0
- 20. 2.Однородные 1)Первой степени: Решаются делением на cos х (или sinx) и методом введения новой переменной. a∙sinx
- 21. 2) Однородные уравнения второй степени: Решаются делением на cos² х (или sin²x) и методом введения новой
- 22. Виды тригонометрических уравнений 3. Уравнение вида: А sinx + B cosx = C. А, В, С
- 23. Виды тригонометрических уравнений 4. Решение тригонометрических уравнений с помощью универсальной тригонометрической подстановки Решаются с помощью введения
- 24. Формулы. Универсальная подстановка. х ≠ π + 2πn; Проверка обязательна! Понижение степени. = (1 + cos2x
- 25. Правила. Увидел квадрат – понижай степень. Увидел произведение – делай сумму. Увидел сумму – делай произведение.
- 26. 1.Потеря корней: делим на g(х). опасные формулы (универсальная подстановка). Этими операциями мы сужаем область определения. 2.
- 27. Решение тригонометрических уравнений по известным алгоритмам Вариант 1. На «3» 3 sin x+ 5 cos x
- 29. Скачать презентацию




















 Лагерь с дневным пребыванием
Лагерь с дневным пребыванием Колыбельные
Колыбельные Детский технопарк Кванториум
Детский технопарк Кванториум Использование СМС технологий в высоконагруженных WEB проектах. Дмитрий Булычков. - презентация
Использование СМС технологий в высоконагруженных WEB проектах. Дмитрий Булычков. - презентация С новым годом, люди!!!
С новым годом, люди!!! Игры в расширенной форме.Информация
Игры в расширенной форме.Информация Кем можно хвалиться?
Кем можно хвалиться? Организационно – педагогические условия эффективности воспитательного процесса в вузе
Организационно – педагогические условия эффективности воспитательного процесса в вузе День Земли
День Земли Швеция в Петербурге
Швеция в Петербурге Презентация на тему Водные ресурсы мира
Презентация на тему Водные ресурсы мира  Н.И Вавилов
Н.И Вавилов Человек в системе экономических отношений
Человек в системе экономических отношений Модель современного менеджмента
Модель современного менеджмента « Сколько весит здоровье ученика?» Составили: ученики 3-б класса Руководитель: Просвирнина Н.П учитель начальных классов МОУ-СОШ№2
« Сколько весит здоровье ученика?» Составили: ученики 3-б класса Руководитель: Просвирнина Н.П учитель начальных классов МОУ-СОШ№2 Давайте дружить
Давайте дружить Город, в котором мы живем
Город, в котором мы живем Паспорт безопасности
Паспорт безопасности Органоиды клетки
Органоиды клетки Дмитрий Сергеевич Мережковский
Дмитрий Сергеевич Мережковский Фазовые переходы
Фазовые переходы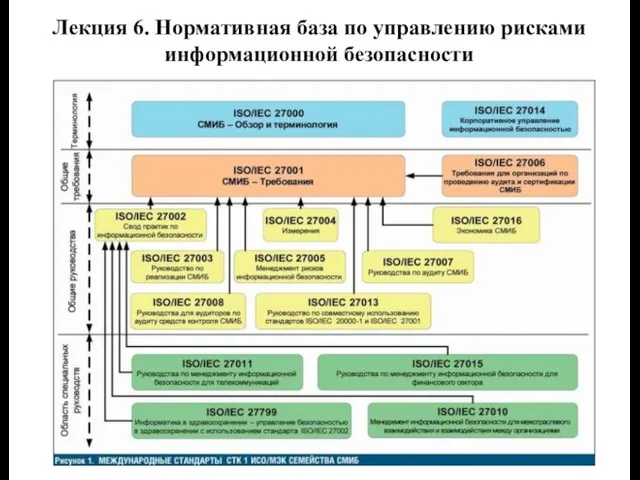 Нормативная база по управлению рисками информационной безопасности. Лекция 6
Нормативная база по управлению рисками информационной безопасности. Лекция 6 Йод
Йод Организация Объдиненных Нациий
Организация Объдиненных Нациий «ЭНЕРГЕТИКА ДОМА».
«ЭНЕРГЕТИКА ДОМА». 9 June 2009
9 June 2009 ТЕХНОЛОГИЯ
ТЕХНОЛОГИЯ Внеклассное мероприятие«Как хорошо, когда мы вместе».
Внеклассное мероприятие«Как хорошо, когда мы вместе».