Презентация на тему Формирование вычислительных навыков. Рациональные способы вычислений

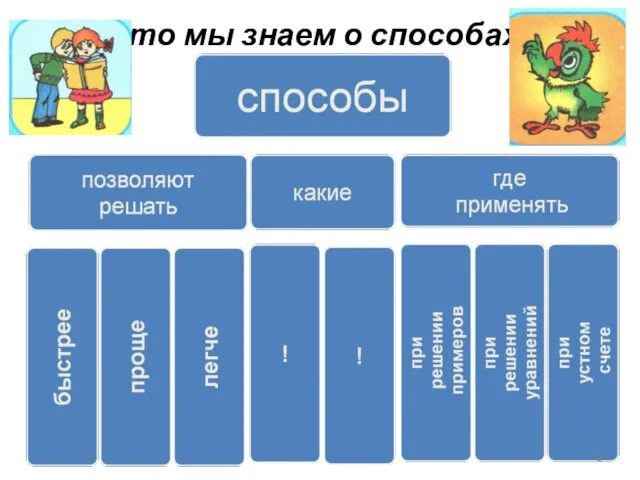
Что мы знаем о способах?

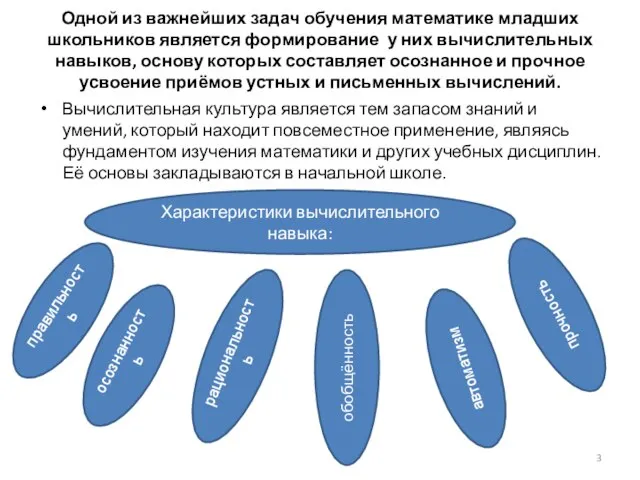
Одной из важнейших задач обучения математике младших школьников является формирование у них вычислительных навыков, основу которых составляет осознанное и прочное усвоение приёмов устных и письменных вычислений.
Вычислительная культура является тем запасом знаний и умений, который находит повсеместное применение, являясь фундаментом изучения математики и других учебных дисциплин. Её основы закладываются в начальной школе.
правильность
рациональность
обобщённость
автоматизм
прочность
осознанность
Характеристики вычислительного навыка:

Остановимся более подробно на таком качестве вычислительного навыка как рациональность, которая напрямую связана с вариативностью.
Рациональность вычислений – это выбор тех вычислительных операций из возможных. «выполнение которых легче других и быстрее приводит к результату арифметического действия».
Знакомство с рационализацией вычислений развивает вариативность мышления, показывает ценность знаний, которые при этом используются. Применение свойств арифметических действий позволяет учителю воспитывать интерес к математике, вызвать у детей желание научиться вычислять наиболее быстрыми и удобными способами. Такой подход позволит поддерживать стремление к использованию математических знаний в повседневной жизни.
Остановлюсь на некоторых из способов вычислений, которые используются на уроках и таких, которые, посильны учащимся , но не всегда используются.

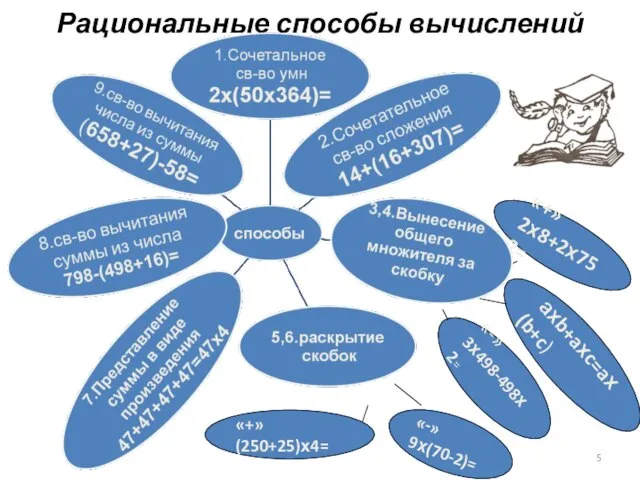
Рациональные способы вычислений
«-»
3х498-498х2=
«+»
2х8+2х752=
ахb+aхc=aх(b+c)
«+»
(250+25)х4=
«-»
9х(70-2)=

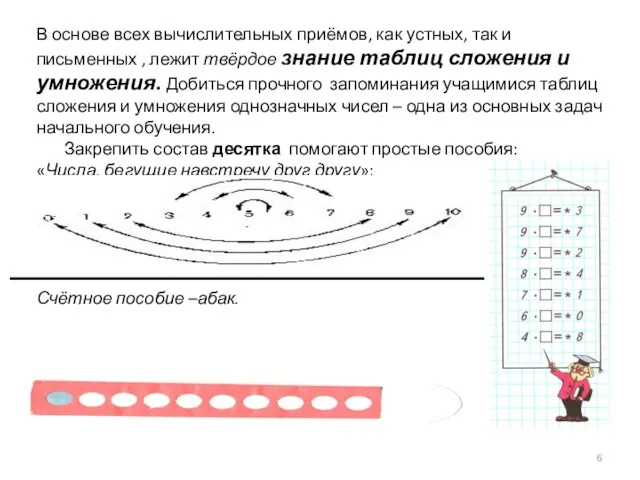
В основе всех вычислительных приёмов, как устных, так и письменных , лежит твёрдое знание таблиц сложения и умножения. Добиться прочного запоминания учащимися таблиц сложения и умножения однозначных чисел – одна из основных задач начального обучения.
Закрепить состав десятка помогают простые пособия:
«Числа, бегущие навстречу друг другу»;
Счётное пособие –абак.

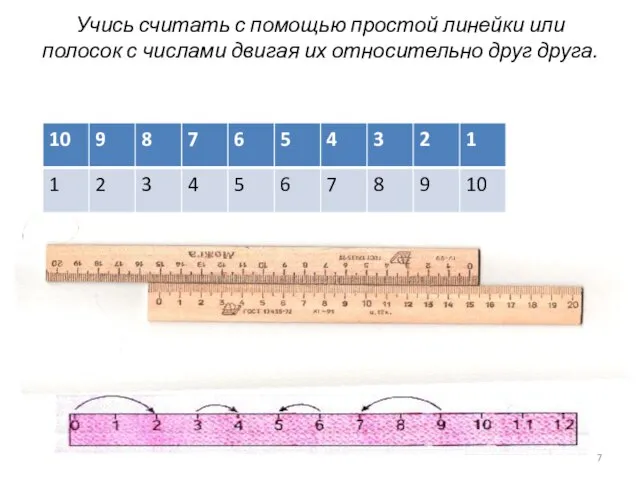
Учись считать с помощью простой линейки или полосок с числами двигая их относительно друг друга.

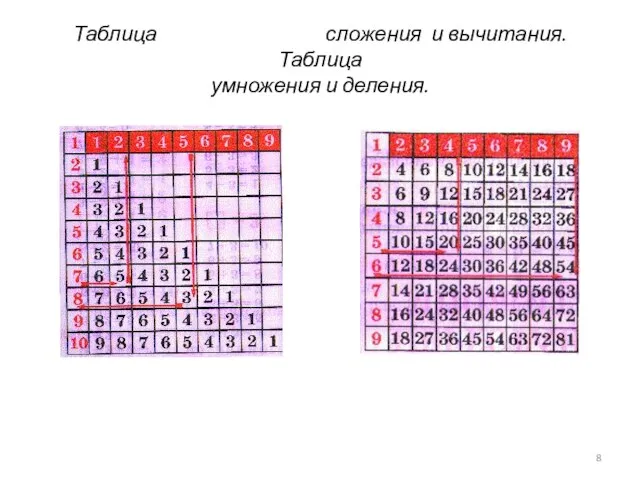
Таблица сложения и вычитания.
Таблица
умножения и деления.

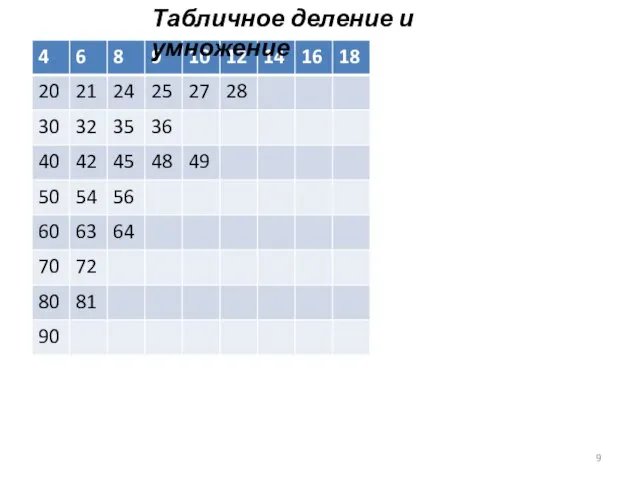
Табличное деление и умножение

Совершенствование навыков устных вычислений зависит не только от методики организации урока, но и во многом от того, насколько дети проявляют интерес к предложенным знаниям. Этот интерес можно вызвать и разнообразными учебными пособиями:
На уроках математики, по теме «Сложение однозначных чисел с переходами через десяток», старые счеты превратила в практическое пособие для детей (на толстую проволоку поместила 10 косточек одного цвета и 10 другого. Дети четко видят десяток.

Мы сами составили таблицу таким образом, что включили в неё все случаи, где ответ (сумма) будет двузначным числом. Сделали заготовку для ответов (заготовили место для каждой из двух цифр).

9 + 6 -1 = 15 8 + 6 -2 = 14
9 + 5 -1 = 14 8 + 5 -2 = 13
После практической деятельности по прибавлению к 9 любого однозначного числа, дети пришли к выводу: «Чтобы к 9 прибавить любое однозначное число достаточно от этого числа отнять 1 и к полученному десятку прибавить остаток»...
Важно, что ребенок сам осознал, что в ответе число единиц получается на один меньше того числа, которое прибавляешь. Дети испытывают радость открытия, общения друг с другом, радость взаимопонимания.
Новый прием развивает воображение, логическое мышление, умение рассуждать.
Этот же принцип действует при сложении 8,7,6 с любым однозначным числом.
На этом пособии удобно прийти к выводу о вычитании из любого двузначного числа (меньше 20)- 9,8,7,6.

Например: 14 – 9 достаточно к единицам прибавить 1 (4+1). Значит 14 – 9 =5
14 – 8 достаточно к единицам прибавить 2 (4+2). Значит 14 - 8= 6.
Так дети легче запоминают таблицу сложения и вычитания.
Чтобы превратить знакомство с таблицей умножения в увлекательное занятие, где ребенок не только исполнитель, но и автор, использую следующий прием. Начинаем с составления подробнейшего анализа таблицы умножения на 9.

ТАБЛИЦА УМНОЖЕНИЯ на 9
1)Определение количества цифр в произведениях от 9х2 до 9х9.
«Прикидка» - во всех произведениях будет по 2 цифры.
Делается заготовка: 9 х 2 = . . . . . 9 х 9 = . .
3)Дети усматривают связь между произведениями: число десятков от произведения к произведению увеличивается на единицу, в то время как число единиц уменьшается:
10 9 х 4 = 36
9 х 2 = 18 9
+1 -1 . . . . . . .
9 х 3 = 27 9 х 9 = 81
Обнаруживают, что сумма цифр произведения при этом равна 9, позже это открытие превращается в признак делимости.
2)Используя несколько способов нахождения произведения: через сумму одинаковых слагаемых, через предыдущее произведение, через представление 9 как 10 – 1, заполняют заготовленные для цифр места.

На следующем этапе они начинают исследовать связь между множителем (отличным от 9) и цифрой десятков, а затем цифрой единиц.
Замечают следующее: число десятков всегда на 1 меньше множителя, т.е. при умножении 9 на 7 в разряде десятков будет 6. 9 х 7 = 63 9 х 8 = 72
-1 -1
А число в разряде единиц дополняет множитель до 10
10 10
9 х 7 = 63 9 х 8 = 72
9 9
(или число десятков до девяти ).

Вывод: чтобы 9 умножить на однозначное число, достаточно от этого числа отнять один и получить десятки, а от 9 отнять количество десятков- получим единицы.
Знакомлю детей также с пальцевым счетом. Располагаем две руки рядом, ладонями к себе. Например: 9x3- загибаем третий палец слева, до согнутого пальца 2 - это десятки, 7 - единицы - получили 27.

Устные приёмы умножения.
Чтобы любое число умножить на 5,достаточно разделить его на 2 и умножить на 10 (т.к. 5-половина 10)
124 х 5 = 124 : 2 х 10 = 620
Чтобы умножить на 50,достаточно число разделить на 2 и умножить на 100 (т.к 50 –половина 100).
36 х 50 = 36 : 2 х 100 = 1800
Чтобы умножить на 25, достаточно число разделить на 4 и умножить на 100 (т.к. 25- четвёртая часть от 100) или наоборот. Если в остатке получится1, то вместо двух нулей поставим 25, если в остатке 2, то – 50,если 3, то – 75.
14 х 25 = 14 : 4 = 3(ост.2), значит 300 + 50 = 350
Чтобы умножить на 125, достаточно число разделить на 8 и умножить на1000(т.к. 125 – восьмая часть от1000)
48 х 125 = 48 : 8 х 1000 = 6000

Чтобы перемножить два одинаковых числа, оканчивающихся на 5, достаточно к первой цифре одного из множителей прибавить 1. Получившееся число умножить на первую цифру второго множителя. Получим число сотен и припишем справа число 25.
75 х 75 = 5625 35 х 35 = 1225
+1 +1
---------------- -----------
8 4
Чтобы умножить на 11, можно умножить на10 и прибавить это же число.
23 х 11 = 23 х 10 + 23 =253
Или: записать последнюю цифру числа в конце произведения, затем сумму последней и предыдущей (и т.д., если цифр в числе несколько), а затем первую цифру числа.
23 х 11 = 2(2+3)3 = 253
243 х 11 = 2(2+4)(4+3)3 =2673
2543 х11 = 2(2+5)(5+4)(4+3)3 = 27973

68 х 99 = 68 х (100 – 1) =68 х 100 – 68 = 6800 – 68 = 6732
47 х 999 = 47 х (1000 – 1) = 47 х 1000 – 47=47000 – 47 = 46953
Но ещё проще ознакомить детей с правилом – « чтобы умножить число на 9 (99, 999) достаточно вычесть из этого числа число его десятков (сотен, тысяч), увеличенное на единицу, и к полученной разности приписать дополнение его цифры единиц до 10 (дополнение до 100 (1000) числа, образованного двумя (тремя) последними цифрами этого числа):
154 х 9 = (154 – 16) х 10 + (10 – 4) = 138 х 10 + 6 = 1380 + 6 = 1386
Умножение на 9, 99, 999
Чтобы умножить число на 9,( 99, 999)достаточно умножить его на 10 (100, 1000) и отнять это же число.
57 х 9 = 57 х 10 – 57 = 570 – 57 = 513

Умножение на 15, 150
При умножении на 15,если число нечётное, умножают его на 10 и прибавляют половину полученного произведения:
23 х 15 = 23 х ( 10 + 5 ) = 230 + 115 = 345;
Если же число чётное , то поступаем ещё проще – к числу прибавляем его половину и результат умножаем на 10:
18 х 15 =( 18 + 9) х 10 = 17 х 10 = 270
При умножении числа на 150 пользуемся тем же приёмом и умножаем результат на 10, т.к. 150 = 15 х 10:
24 х 150 = ( (24 + 12) х 10 ) х 10= (36 х 10) х 10 = 3600
Интересно, что 7 х 11 х 13 = 1001 (число Шехерезады)
7 х 143 = 1001
11 х 91 = 1001
77 х 13 = 1001

Признаки делимости.
: на 2 – чётные числа, круглые.
: на 3 – сумма цифр которых делится на 3.
: на 4 – две последние цифры составляют число, которое делится на 4 и числа, у которых два нуля на конце.
: на 5 числа, у которых на конце 5 или 0.
: на 6 числа, которые делятся и на 2 и на 3.
: на 8 числа, в записи которых три последние цифры образуют число ,делящееся на8.
: на 9 числа, сумма цифр которых делится на 9.
: на 10 числа, которые оканчиваются на 0.
: на 11 числа, если из суммы цифр, стоящих на нечётных местах вычесть сумму цифр на чётных местах получится 0 или число кратное 11. 87635064 8+6+5+6=25
7+3+0+4=14 25-14=11,
значит всё число делится.

Для малых чисел: число справа налево делят по 2 цифры и складывают. Если сумма делится на11, то всё число делится.
528 5 + 28 =33, значит делится.
: на12 числа, которые делятся и на 4, и на 3.
: на14 числа, которые делятся и на 7, и на 2.
: на 15 числа, которые делятся и на 3, и на 5.

Рационализация вычислений:
1) за счёт тождественного преобразования:
7584 : 6 -1584 : 6 = (7584 – 1584) : 6
1476 + 65 + 24 + 35 = ( 1476 +24) + (65 +35)=
2) за счёт возможности не выполнять некоторые арифметические действия:
104482 : 6 – 104482 : 6 = 0
(75840 : 20) х 20 = 75840
Свойства арифметических действий и конкретный смысл умножения
1) 120: ( 5 х 3) = 120 : 5 : 3
2) 630: 2 : 5 = 630 : (2 х 5)
3) 57 х 9 + 57 =57 х (9 + 1)
4) 4 х 35 х 25 х 2 = (4 х 25) х (35 х 2)

Возможность: устно вычислить
5300 : 2 : 5 = 5300 : (2 х 5)
Выполнять меньшее количество действий
30452 х 3 х 2 =30452 х (3 х 2)
6532 х 3 + 3645 х 3 = (6532 + 3645) х 3
Проще вычислять
70 : 2 + 80 : 2 = (70 + 80) : 2
Связь результатов и компонентов действий
(91010 – 57654) + 57654 = 91010 –увеличили и уменьшили на столько же
Конкретный смысл выполнения вычитания и деления над одинаковыми компонентами
а – а = 0 а : а = 0
(304 + 629) – (304 + 629) = 0 -одинаковые суммы
Умножение на нуль , случаи умножения и деления 0.
а х 0 = 0 0 х а = 0 0 : а = 0
283 х (4704 - 676) х 0 = 0

Представление некоторых одинаковых чисел одинаковыми выражениями
(12004 – 4 х 19 ) + 4 х 19 = 12004
Представление нуля или одного из одинаковых чисел выражением:
( 12004 – 4 х 19 ) + 17= (12004 – 76 ) + 76 = 12004
( 100 – 99 – 1) х (1723 – 23 х 13) = 0 х (1723 – 23 х 17) = 0
Возможность применения знаний не ко всему выражению, а к его части:
2380 + 2527 : 7 + 273 : 7 = 2380 + (2527 + 273) : 7 = 2380 + 2800 : 7 =
=2380 + 400 = 2780
Возможность применять одновременно несколько знаний к разным частям выражения:
5 х 23 х 2 + 98 + 102 = (5 х 2) Х 23 + (98 + 102) = 230 + 200 = 430
783 х 4 + 783 х 6 – 703 х 8 х 0 = 783 х ( 4 + 6) – 0 = 7830
Возможность применения к одному выражению нескольких знаний – одного после другого.
5 х ( 300 + 65) – 5 х 65 =5 х 300 + 5 х 65 – 5 х 65 = 5 х 300 =1500
65277 : 3 : 3 – 65277 : 9 =65277 : ( 3 х 3) – 65277 : 9 = 65277 : 9 -65277 : 9 = 0

Приём замены множителя разностью
Приём замены второго множителя, если этот множитель на 1-2
единицы меньше двузначного или трёхзначного разрядного числа:
68 х 5 = (70 -2) х 5 = 70 х 5 – 2 х 5 = 350 -10 = 340
599 х 8 = (600- 1) х 8 =600 х 8 – 8 = 4800 – 8 = 4792
Приём замены множителя произведением:
35 х 6= 35 х ( 2 х 3) = (35 х 2) х 3 = 70 х 3 = 210
125 х 48 = 125 х (8 х 6) = ( 125 х 8) х 6 = 1000 х 6 = 6000

Умножение двузначных чисел.
Основой умножения двузначных чисел является правило умножения суммы на число. 18 х 16 . Сначала число 18 представим в виде «суммы удобных (разрядных) слагаемых ,затем используем распределительный закон умножения относительно сложения:
18 х 16 =(10 + 8) х 16=10 х 16 + 8 х 16 = 160 + 128 = 288
Устно можно проще: к одному из чисел надо прибавить количество единиц другого, эту сумму умножить на 10 и прибавить к ней произведение единиц данных чисел:
18 х 16 = (18 + 6) х 10 + 8 х 6 = 240 + 48 =288
Таким способом можно умножать двузначные числа , меньше 20, а также числа ,в которых одинаковое количество десятков:
23 х 24 = (23 + 4) х 20 + 4 х 3 = 27 х 20 + 12 =540 + 12 = 562

Приём округления, основанный на изменении результата вычисления при изменении одного или нескольких компонентов.
1. Сложение. Для нахождения значения суммы используется приём округления одного или нескольких слагаемых.
При увеличении (уменьшении) слагаемого на несколько единиц, сумму уменьшаем (увеличиваем) соответственно на столько же единиц:
324 + 48 = 324 + (48 + 2) – 2= (324 + 50) -2 = 374– 2 = 372 или
324 + 48 = (320+ 50) + 4 – 2 = 370 + 4 – 2 = 372
2. Вычитание.
1) при увеличении (уменьшении) уменьшаемого на несколько единиц разность уменьшаем (увеличиваем) на столько же единиц:
497 – 36 = (500 – 36) – 3 =464 – 3=461;
2) при увеличении (уменьшении) вычитаемого на несколько единиц разность увеличиваем (уменьшаем) на столько же единиц:
534 – 98 = (534 – 100) + 2 = 434 + 2 = 436

3)При увеличении ( уменьшении) уменьшаемого и вычитаемого на несколько единиц разность не изменяется:
231 – 96 = (231 + 4) – (96 +4) = 235 – 100 = 135
3. Умножение.
При увеличении ( уменьшении) одного из множителей на несколько единиц умножаем полученное целое число и прибавленные (отнятые) единицы на другой множитель и из первого произведения вычитаем второе произведение (полученные произведения складываем).
97 х 6 = (100 – 3 ) х 6 = 100 х 6 – 3 х 6 = 600 – 18 = 582

Некоторые способы вычислений могут показаться сложными, но при правильной организации работы на уроке и внеклассных занятиях учащиеся осваивают их и с удовольствием используют в вычислительной деятельности. Привычка выполнять подобные вычисления устно формирует устойчивый навык, который не раз сыграет добрую службу при изучении более сложного материала.
Вариативность вычислительных навыков учащихся формирует интерес, положительную мотивацию к вычислительной деятельности, даёт возможность знакомить школьников с известными вычислительными секретами, показать практическую значимость математики, тогда перед детьми откроется совсем другая математика – живая, полезная и понятная.