Слайд 2 Вид урока: урок – проект. Тип урока: обобщение и систематизация знаний

с элементами исследования и организации проектной деятельности.
Цели урока:
Образовательные: обобщить и систематизировать знания учащихся о модуле и его свойствах; умения решать различные уравнения, содержащие модуль и уравнения, приводимые к уравнениям, содержащим модуль.
Развивающие: развивать творческую и мыслительную деятельность учащихся, навыки проектно-исследовательской деятельности, способствовать формированию навыков коллективной работы, развивать умение чётко и ясно излагать свои мысли.
Воспитательные: формирование интереса к предмету посредством вовлечения их в проектную деятельность, способствовать формированию навыков взаимодействия в малых группах.
Слайд 3Проект -
это специально организованный учителем и самостоятельно выполняемый учащимися комплекс действий,

завершающихся созданием творческого продукта.
Слайд 4Определение модуля
Свойства
модуля

Слайд 5Геометрический смысл модуля
Геометрически есть расстояние от точки х числовой оси до начала

отсчёта – точки О.
есть расстояние между точками х и а числовой оси.
Слайд 8Инструкция по работе над проектом.
1. Решить уравнения.
2. Проанализировать способы решения.
3. Провести

классификацию данных уравнений:
а) сгруппировать примеры по способам решения;
б) определить, в чём заключается общий вид уравнений в каждой группе;
в) дать название каждой группе уравнений.
4. Создать проект таблицы: « Решение уравнений, содержащих модуль».
5. Подготовить защиту проекта.
Слайд 9Защита проектов.
. Оценочный лист. (5-бальная система)
Владеет докладчик терминологией, которую использует в своём

проекте
Смог докладчик проекта доказать, что разработанная группой структура самая оптимальная для решения поставленной задачи
Выполнила ли группа все поставленные перед ней задачи
Творческие способности докладчика
Оформление проекта
Слайд 10Простейшие уравнения вида ,b>0.
По определению модуля
1.
Ответ: -19;21.

Слайд 11Уравнения более общего вида
Условие

Слайд 13Уравнения, приводимые к уравнениям, содержащим модуль.
Иррациональное уравнение

Слайд 14Уравнения, приводимые к уравнениям, содержащим модуль
Логарифмическое уравнение

Слайд 15Иррациональные уравнения, содержащие модуль.
В силу того, что модуль раскрывается однозначно.

Слайд 17Иррациональные уравнения, содержащие модуль.
В силу того, что модуль раскрывается двузначно.
Ответ: -4,5;

-0,75; 0.
Слайд 19Уравнения, содержащие несколько модулей.
( Решаемые с помощью метода интервалов)
1.Найдём значения х,

при которых значения выражений, стоящих под знаком модуля, равны 0:
х -1 = 0 при х = 1.
х – 2=0 при х = 2.
2. Эти значения разбивают ОДЗ на промежутки:
3.Запишем на каждом из промежутков данное уравнение без знаков модуля.
Получим совокупность систем.
Слайд 20Уравнение, содержащее несколько модулей.
Метод интервалов

Слайд 221.Простейшее уравнение,
содержащее модуль, где b>0:
2.Уравнение более общего вида, содержащее

модуль:
Слайд 23Уравнение вида
По определению модуля

Слайд 24 Уравнения, приводимые к уравнениям, содержащим модуль.
1

Слайд 25Уравнения, содержащие несколько модулей
и те, которые не сводятся к виду │f(x)

│= g(x) решаются с помощью метода интервалов:
1.Найдём значения x, при которых значение выражений, стоящих под знаком модуля, равны нулю.
2.Найденные значения x разбивают ОДЗ на промежутки.
3.Запишем на каждом из промежутков уравнение без знаков модуля. Получим совокупность систем.























 Компьютер и здоровье глаз
Компьютер и здоровье глаз Пейзаж.Времена года
Пейзаж.Времена года Организационное и информационное обеспечение фандрейзинга
Организационное и информационное обеспечение фандрейзинга Сложноподчиненное предложение. Повторение и обобщение изученного.
Сложноподчиненное предложение. Повторение и обобщение изученного. История радио и мобильной связи
История радио и мобильной связи А как ты знаешь физику?
А как ты знаешь физику? Презентация на тему Нефтяная промышленность
Презентация на тему Нефтяная промышленность  Изобразительное искусство барокко
Изобразительное искусство барокко Как начать бизнес в интернете?
Как начать бизнес в интернете? Sony Ericsson: Из VGA в HD
Sony Ericsson: Из VGA в HD Символика Краснодарского края
Символика Краснодарского края Для умных женщин Одна супружеская пара поехала в выходные на озеро порыбачить.
Для умных женщин Одна супружеская пара поехала в выходные на озеро порыбачить. Бюджет для граждан по Решению Совета депутатов МО Александровский район от 23.12.2020
Бюджет для граждан по Решению Совета депутатов МО Александровский район от 23.12.2020 Children's behavior and its influence on their future acts
Children's behavior and its influence on their future acts РАНХиГС_очно_27.09.2022_Акцнт, реф, защ, техн ОС
РАНХиГС_очно_27.09.2022_Акцнт, реф, защ, техн ОС Слова-паразиты, или экология речи
Слова-паразиты, или экология речи Иммунная система и канцерогенез
Иммунная система и канцерогенез  Подарки AI Journey. Предложения. Сберклауд
Подарки AI Journey. Предложения. Сберклауд Философские теории неврозов
Философские теории неврозов Реализация и изучение игры «Жизнь» в среде электронных таблиц (MS Ecxel)
Реализация и изучение игры «Жизнь» в среде электронных таблиц (MS Ecxel) Деструктивность учащегося и образовательной среды: точки соприкосновения
Деструктивность учащегося и образовательной среды: точки соприкосновения БАЛАНС-2W: ПОДГОТОВКА СПРАВКИ 2-НДФЛ
БАЛАНС-2W: ПОДГОТОВКА СПРАВКИ 2-НДФЛ Подготовка граждан к военной службе
Подготовка граждан к военной службе Ультразвуковые накладные расходомеры Flexim
Ультразвуковые накладные расходомеры Flexim Презентация для заказных проектов
Презентация для заказных проектов Поступление на государственную службу
Поступление на государственную службу Оценка достижений учащихся в разновозрастной группе
Оценка достижений учащихся в разновозрастной группе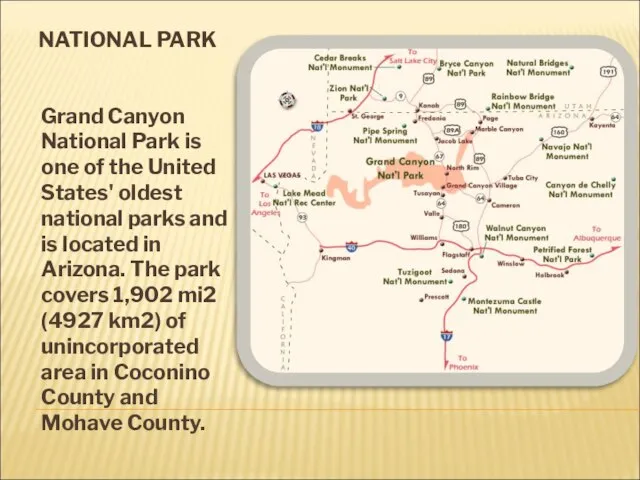 Grand Canyon National Park
Grand Canyon National Park