Решение задач на повторение

Тема урока:
Решение задач на повторение
( из сборника заданий для проведения экзамена в 9 классе)
Цели:
Формировать умение решать задачи по геометрии;
Развивать творческое мышление, устную и письменную речь;
Воспитывать готовность к преодолению трудностей в процессе учебного труда.
Готовить учащихся к профильному экзамену

Решение задач на темы:
Подобие треугольников;
Трапеция;
Внешний угол треугольника;
Центральные и вписанные углы.

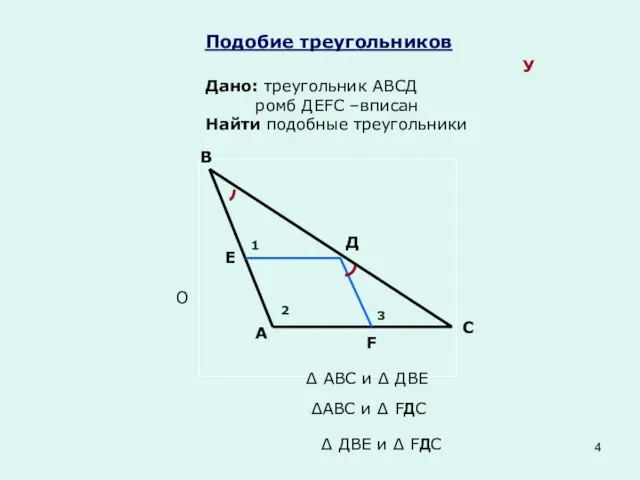
Подобие треугольников
У
Дано: треугольник АВСД
ромб ДЕFС –вписан
Найти подобные треугольники
В
А
С
Д
Е
F
∆ АВС и ∆ ДВЕ
1
2
∆АВС и ∆ FДС
∆ ДВЕ и ∆ FДС
3
О

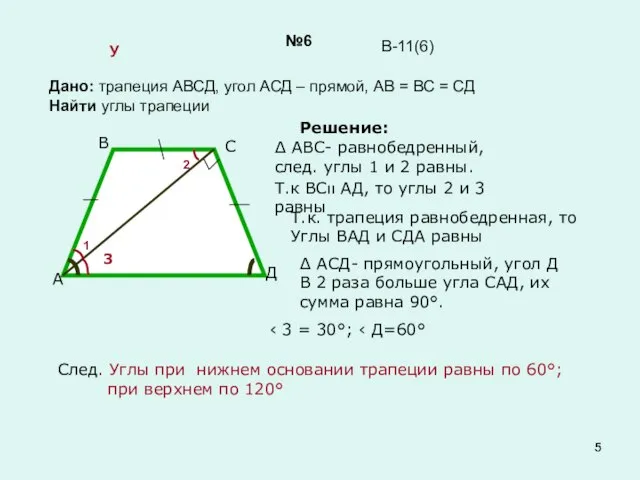
№6
Дано: трапеция АВСД, угол АСД – прямой, АВ = ВС = СД
Найти углы трапеции
В-11(6)
У
А
В
С
Д
Решение:
∆ АВС- равнобедренный,
след. углы 1 и 2 равны.
Т.к. трапеция равнобедренная, то
Углы ВАД и СДА равны
Т.к ВСװ АД, то углы 2 и 3 равны
3
∆ АСД- прямоугольный, угол Д
В 2 раза больше угла САД, их
сумма равна 90°.
‹ 3 = 30°; ‹ Д=60°
След. Углы при нижнем основании трапеции равны по 60°;
при верхнем по 120°
1
2

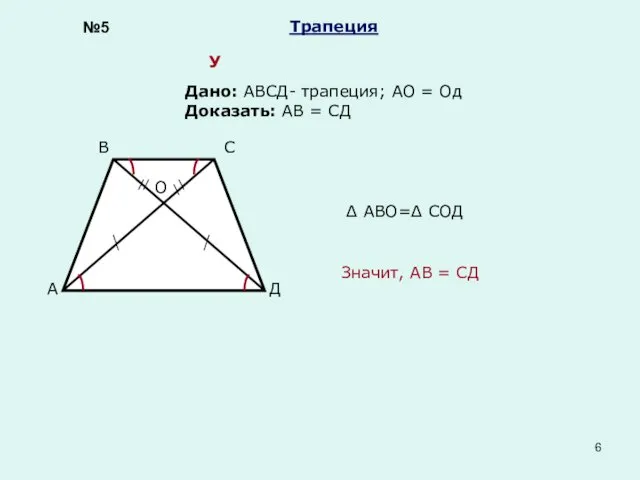
Трапеция
Дано: АВСД- трапеция; АО = Од
Доказать: АВ = СД
А
В
С
Д
О
У
∆ АВО=∆ СОД
Значит, АВ = СД
№5

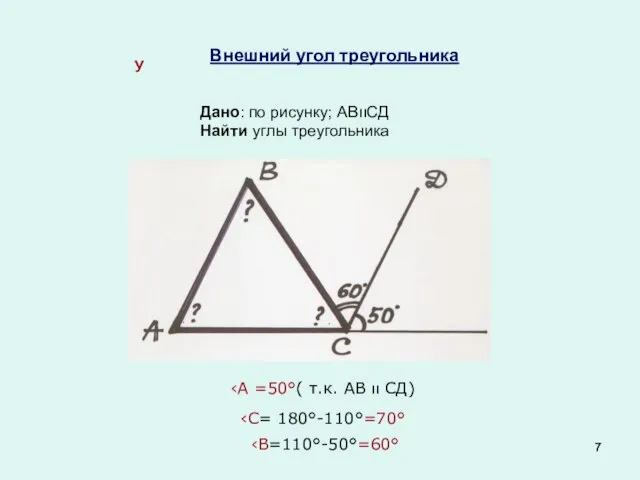
Внешний угол треугольника
Дано: по рисунку; АВװСД
Найти углы треугольника
У
‹А =50°( т.к. АВ װ СД)
‹С= 180°-110°=70°
‹В=110°-50°=60°

Решаем письменно
В-3(4)
В-10(5)
В-18(1)
В-10(9)
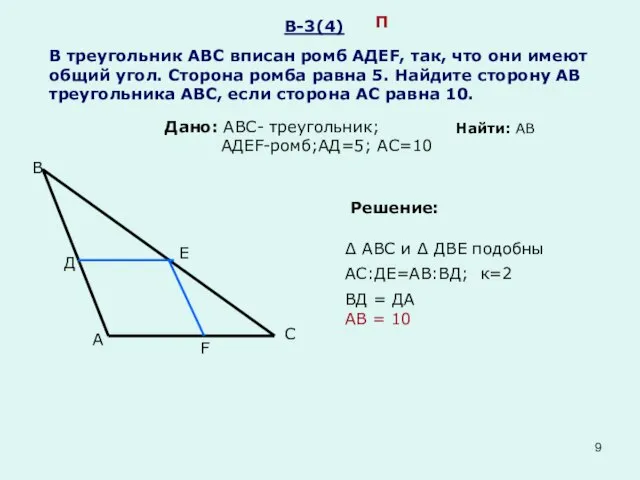
В-14(9)

В-3(4)
В треугольник АВС вписан ромб АДЕF, так, что они имеют
общий угол. Сторона ромба равна 5. Найдите сторону АВ
треугольника АВС, если сторона АС равна 10.
А
В
С
Д
Е
F
П
Дано: АВС- треугольник;
АДЕF-ромб;АД=5; АС=10
Решение:
∆ АВС и ∆ ДВЕ подобны
АС:ДЕ=АВ:ВД; к=2
ВД = ДА
АВ = 10
Найти: АВ

№3 В-10(5)
Дано: трапеция АВСД –прямоуг. АС – биссектриса ВС=10; АД=16
Найти: а) СД; б)периметр АВСД; в)площадь АВСД
А
В
С
Д
Решение:
10
16
Н
1
2
Углы 1 и 3 равны
∆ АВС- равнобедренный
АВ = ВС =10
ВН -высота
Рассм.∆ АВН
АН= АД-ВС=16-10=6
ВН из ∆ АВН по теореме Пифагора ВН= АВ -АН=100-36=64
ВН=8; сл. СД=8
а)
б) Р= 10+10+8+16=44; Р=44
в)
S =
S = (16+10)/2 ∙8 =104; s = 104
3

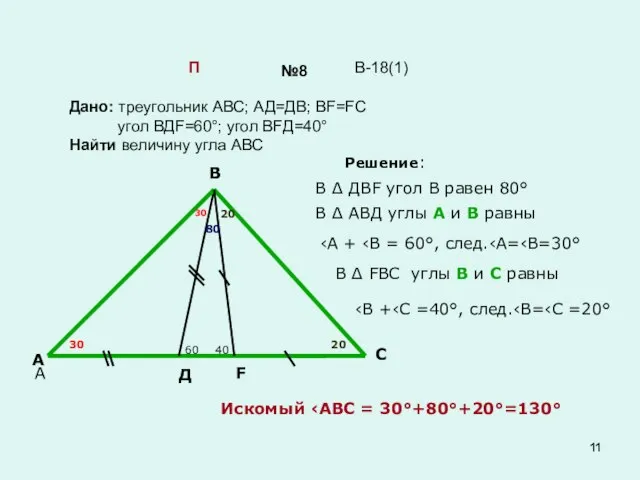
№8
Дано: треугольник АВС; АД=ДВ; ВF=FC
угол ВДF=60°; угол ВFД=40°
Найти величину угла АВС
В-18(1)
П
А
В
С
А
Д
F
60
40
Решение:
В ∆ ДВF угол В равен 80°
80
В ∆ АВД углы А и В равны
‹А + ‹В = 60°, след.‹А=‹В=30°
30
30
В ∆ FВС углы В и С равны
‹В +‹С =40°, след.‹В=‹С =20°
20
20
Искомый ‹АВС = 30°+80°+20°=130°

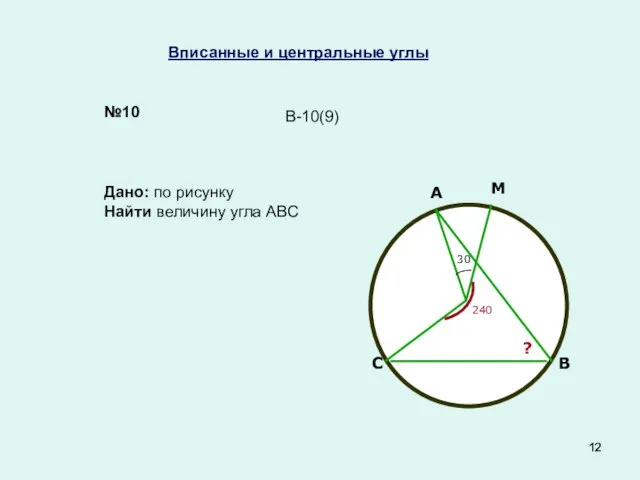
Вписанные и центральные углы
№10
Дано: по рисунку
Найти величину угла АВС
В-10(9)
С
А
М
В
240
30
?

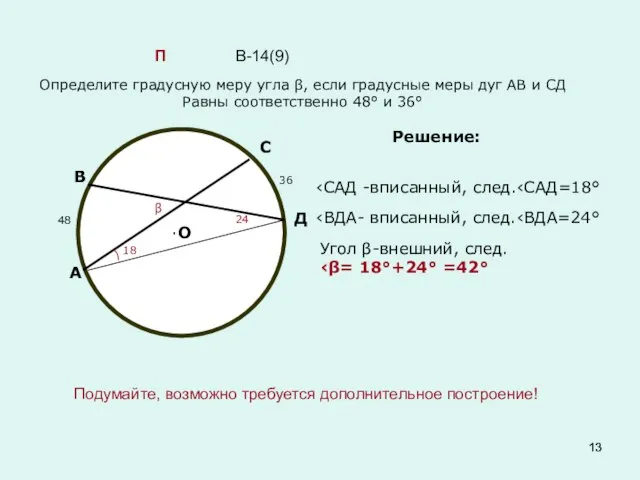
В-14(9)
Подумайте, возможно требуется дополнительное построение!
П
Определите градусную меру угла β, если градусные меры дуг АВ и СД
Равны соответственно 48° и 36°
∙О
В
А
С
Д
48
36
β
‹САД -вписанный, след.‹САД=18°
Решение:
18
‹ВДА- вписанный, след.‹ВДА=24°
24
Угол β-внешний, след.
‹β= 18°+24° =42°

Самостоятельно решить задачи из тестов
№1; №2; №4; №7; №9

Проверим решение задач

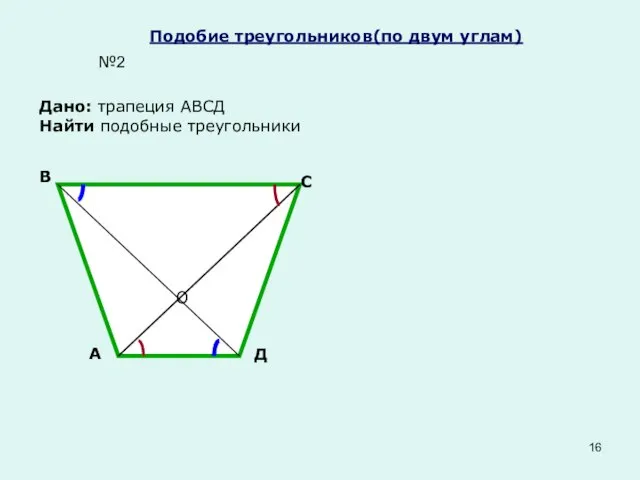
Подобие треугольников(по двум углам)
Дано: трапеция АВСД
Найти подобные треугольники
№2
А
В
С
Д
О

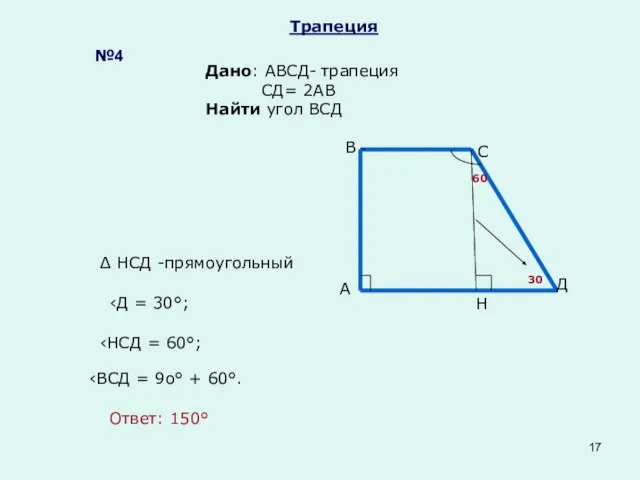
Трапеция
Дано: АВСД- трапеция
СД= 2АВ
Найти угол ВСД
№4
А
В
С
Д
Н
‹Д = 30°;
‹НСД = 60°;
‹ВСД = 9о° + 60°.
Ответ: 150°
∆ НСД -прямоугольный
30
60

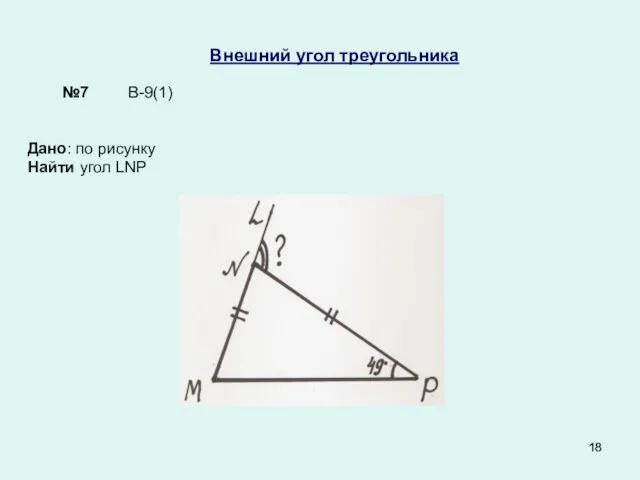
Внешний угол треугольника
Дано: по рисунку
Найти угол LNP
В-9(1)
№7

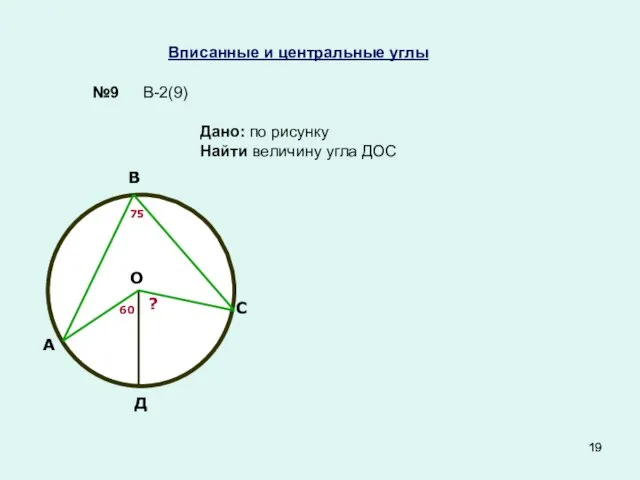
Вписанные и центральные углы
№9
Дано: по рисунку
Найти величину угла ДОС
В-2(9)
А
В
С
О
75
60
Д
?

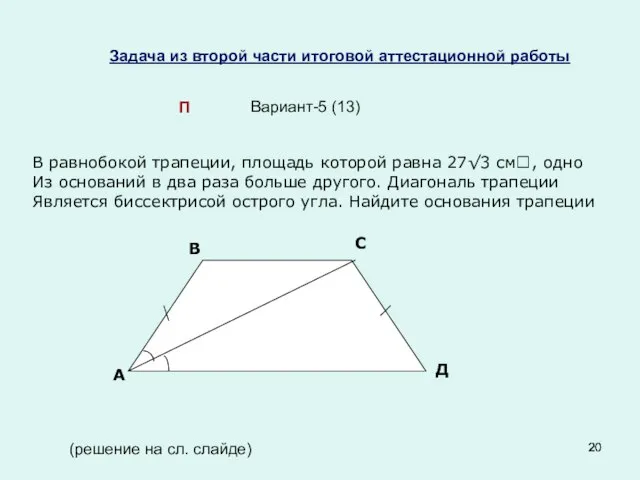
Задача из второй части итоговой аттестационной работы
Вариант-5 (13)
П
(решение на сл. слайде)
В равнобокой трапеции, площадь которой равна 27√3 см, одно
Из оснований в два раза больше другого. Диагональ трапеции
Является биссектрисой острого угла. Найдите основания трапеции
А
В
С
Д

В равнобокой трапеции, площадь которой равна 27√3 см², одно из оснований в два раза больше другого. Диагональ трапеции является биссектрисой острого угла. Найдите основания трапеции.
АС- биссектриса угла ВАД, значит
∆АВС- равнобедренный, ВС=АВ=СД
Пусть ВС=х, АД=2х
КД=(АД-ВС):2=х/2
Из ∆ СКД
ВС=6 см, АД=12 см
й

Домашнее задание
Решить задачи из сборника заданий для проведения экзамена
и подготовиться к выполнению тестирования по пройденным
на уроке темам
Подобные треугольники: В-1(4); В-2(4); В-3(2)
Трапеция: В-3(7); В-6(5);
Внешний угол треугольника: В-13(1) В-15(1)
Вписанные и центральные углы: В-3(9); В-18(9); В-19(9)

Приложение
(решение задач из 2 части сборника на тему трапеция)

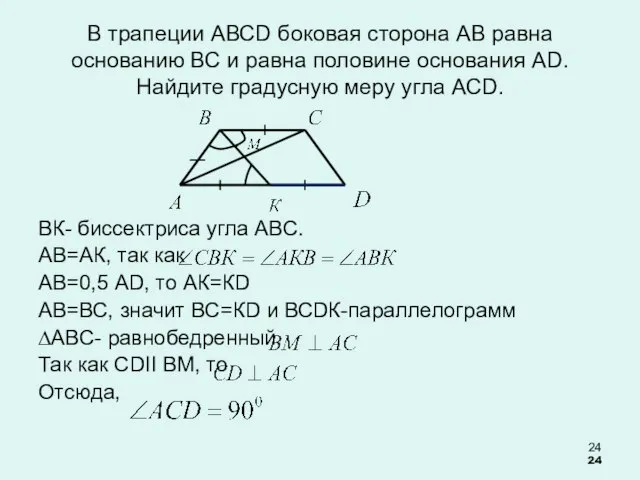
В трапеции АВСD боковая сторона АВ равна основанию ВС и равна половине основания АD. Найдите градусную меру угла АСD.
ВК- биссектриса угла АВС.
АВ=АК, так как
АВ=0,5 АD, то АК=КD
АВ=ВС, значит ВС=КD и ВСDК-параллелограмм
∆АВС- равнобедренный,
Так как СDІІ ВМ, то
Отсюда,

Найдите площадь трапеции, основания которой 16 см и 28 см, а диагонали 17 см и 39 см.
16 cм
28 см
Проведем СКІІ ВD
DВСК- параллелограмм, значит ВС=DК, СК=DВ
В ∆АСК АС=17 см, СК=ВD=39 см, АК=28+16=44(см)
Найдем площадь АСК по формуле Герона
p= (17+39+44):2=50,
S=330 см²
так как, следовательно,

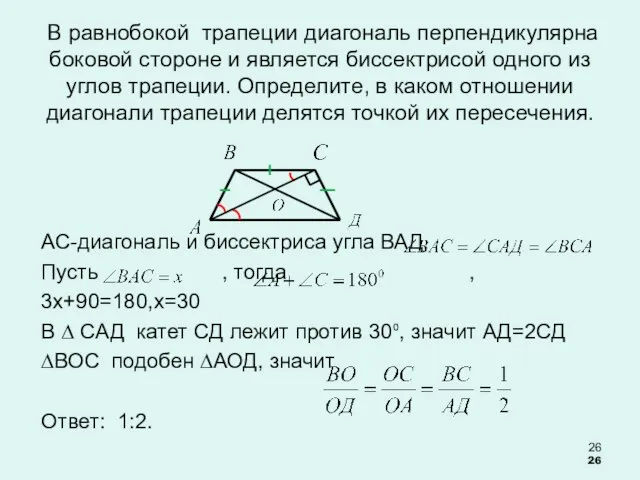
В равнобокой трапеции диагональ перпендикулярна боковой стороне и является биссектрисой одного из углов трапеции. Определите, в каком отношении диагонали трапеции делятся точкой их пересечения.
АС-диагональ и биссектриса угла ВАД,
Пусть , тогда ,
3х+90=180,х=30
В ∆ САД катет СД лежит против 30⁰, значит АД=2СД
∆ВОС подобен ∆АОД, значит
Ответ: 1:2.