лука», «струна». Индийские ученые впервые предложили рассматривать величину полухорды (синуса), которую называли архаджива, что буквально означает «половина тетивы лука», но потом стали называть джива, что значит «тетива лука».
Как по примеру индийских математиков не увидеть на рис. 9 лук с натянутой стрелой?
Арабские математики, которые позже (начиная с VIII в.) осваивали накопленные математические знания, писали слово джива в арабской транскрипции как джиба, что созвучно арабскому слову джайб, которое дословно означает «пазуха».
Вместе с военными завоеваниями арабов слово «пазуха» для обозначения полухорды в тригонометрии попало в Европу (X—XII вв.), где европейские ученые перевели его на латынь как «синус».
Греческое слово хорде, от которого происходит наш термин «хорда», буквально означает «тетива лука», «струна». Индийские ученые впервые предложили рассматривать величину полухорды (синуса), которую называли архаджива, что буквально означает «половина тетивы лука», но потом стали называть джива, что значит «тетива лука».
Как по примеру индийских математиков не увидеть на рис. 9 лук с натянутой стрелой?
Арабские математики, которые позже (начиная с VIII в.) осваивали накопленные математические знания, писали слово джива в арабской транскрипции как джиба, что созвучно арабскому слову джайб, которое дословно означает «пазуха».
Вместе с военными завоеваниями арабов слово «пазуха» для обозначения полухорды в тригонометрии попало в Европу (X—XII вв.), где европейские ученые перевели его на латынь как «синус».















 Маркетинговое планирование
Маркетинговое планирование Психологическая подготовка к всероссийской олимпиаде профессионального мастерства. 2021г
Психологическая подготовка к всероссийской олимпиаде профессионального мастерства. 2021г ЗНАЧЕНИЕ МИРОВОГО ОКЕАНА В ЖИЗНИ ЛЮДЕЙ
ЗНАЧЕНИЕ МИРОВОГО ОКЕАНА В ЖИЗНИ ЛЮДЕЙ Ночь искусств. Театр как вид искусства
Ночь искусств. Театр как вид искусства Герои Чернушки
Герои Чернушки Фотография авангарда
Фотография авангарда Здоровье – ни с чем не сравнимая ценность. 5 класс
Здоровье – ни с чем не сравнимая ценность. 5 класс На востоке встаёт луна, На западе гаснет солнце, А ветка вишни моей цветёт. Суворова Альбина 8 класс, школа 541
На востоке встаёт луна, На западе гаснет солнце, А ветка вишни моей цветёт. Суворова Альбина 8 класс, школа 541 Юные герои Первой мировой войны
Юные герои Первой мировой войны Методика проведения международных маркетинговых исследований Дисциплина: Международный маркетинг Преподаватель: профессор ка
Методика проведения международных маркетинговых исследований Дисциплина: Международный маркетинг Преподаватель: профессор ка Презентация на тему Скульптура Древнего Рима
Презентация на тему Скульптура Древнего Рима  Переобучение, повышение квалификации женщин, находящихся в отпуске по уходу за ребенком
Переобучение, повышение квалификации женщин, находящихся в отпуске по уходу за ребенком Международно-правовое регулирование охраны труда
Международно-правовое регулирование охраны труда Бандажна проходка
Бандажна проходка Дмитрий Иванович Мендилеев
Дмитрий Иванович Мендилеев Персоналии в отечественной социальной психологии
Персоналии в отечественной социальной психологии Презентация на тему Презентации Омар Хайям
Презентация на тему Презентации Омар Хайям Тепло из недр Земли
Тепло из недр Земли Успешный опыт использования поисковой интернет- рекламы в продажах садовой техники - ООО «Садторг» (www.dom-sad.ru, www.tehnosad.ru)www.dom-sad.ruwww.tehnos
Успешный опыт использования поисковой интернет- рекламы в продажах садовой техники - ООО «Садторг» (www.dom-sad.ru, www.tehnosad.ru)www.dom-sad.ruwww.tehnos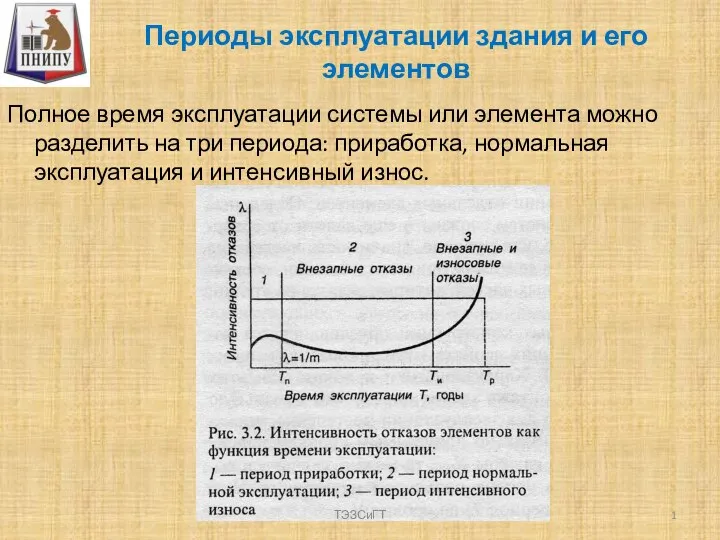 Периоды эксплуатации здания и его элементов
Периоды эксплуатации здания и его элементов Подборка телерекламы из Интернета по объекту рекламирования
Подборка телерекламы из Интернета по объекту рекламирования Когнитивные особенности младенца
Когнитивные особенности младенца Практика защиты авторских прав для произведений в интернете
Практика защиты авторских прав для произведений в интернете Презентация на тему Водные ресурсы мира (10 класс)
Презентация на тему Водные ресурсы мира (10 класс) Работа выполнена в рамках проекта «Повышение квалификаций различных категорий работников образования и формирование у них базов
Работа выполнена в рамках проекта «Повышение квалификаций различных категорий работников образования и формирование у них базов Компьютерный дизайн как профессия
Компьютерный дизайн как профессия БАСНИ- «КНИГА МУДРОСТИ САМОГО НАРОДА» (Н.В.ГОГОЛЬ)
БАСНИ- «КНИГА МУДРОСТИ САМОГО НАРОДА» (Н.В.ГОГОЛЬ) Производитель комплектующих для промышленной вентиляции
Производитель комплектующих для промышленной вентиляции