С5 2012г.

Работа
Учителя математики
Зениной Алевтины Дмитриевны
Найти наименьшее значение параметра, при котором система неравенств, задающие на координатной плоскости круг,
имеет единственное решение .
С5 Вариант 7 2012 год.

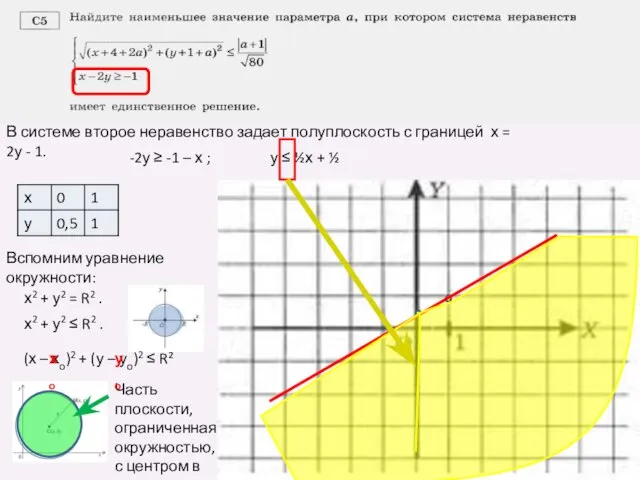
В системе второе неравенство задает полуплоскость с границей х = 2у - 1.
-2у ≥ -1 – х ;
у ≤ ½х + ½
Вспомним уравнение окружности:
х2 + у2 ≤ R2 .
х2 + у2 = R2 .
(х – хо)2 + (у – уо)2 ≤ R²
Часть плоскости,
ограниченная
окружностью,
с центром в точке
А(хо;уо).
хо
уо

Преобразуем первое неравенство:
Первое неравенство задает на координатной плоскости круг радиуса
С центром в точке (-4-2ɑ ; -1-ɑ)
Система имеет единственное решение, если круг и полуплоскость имеют одну общую точку.
Следовательно расстояние от центра круга до прямой у = ½х + ½
равно радиусу круга.
Это расстояние между параллельными прямыми:
у = ½х + ½ и какой-то прямой у = ½х + b, проходящей
через центр круга
Прямые параллельны, то k1 = k2 .
у =½х + b это уравнение
прямой проходящей через центр круга
Из первого неравенства получаем:
Подставим в это уравнение прямой вместо х и у наши значения хо и уо .

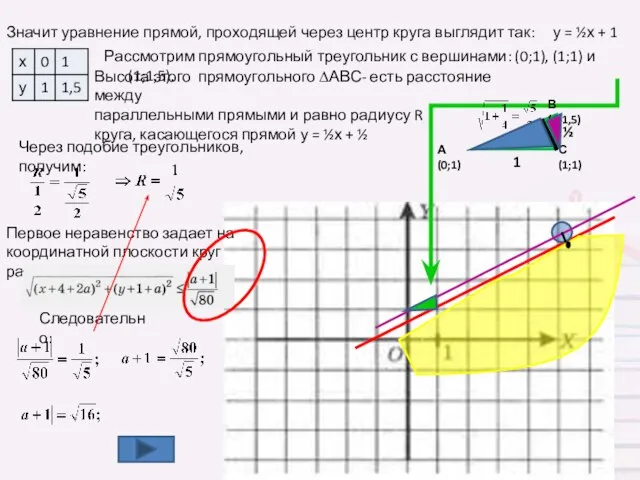
Значит уравнение прямой, проходящей через центр круга выглядит так: у = ½х + 1
Рассмотрим прямоугольный треугольник с вершинами: (0;1), (1;1) и (1;1,5).
С(1;1)
В(1;1,5)
А(0;1)
½
1
Высота этого прямоугольного ∆АВС- есть расстояние между
параллельными прямыми и равно радиусу R
круга, касающегося прямой у = ½х + ½
Через подобие треугольников, получим:
Первое неравенство задает на
координатной плоскости круг радиуса
Следовательно:

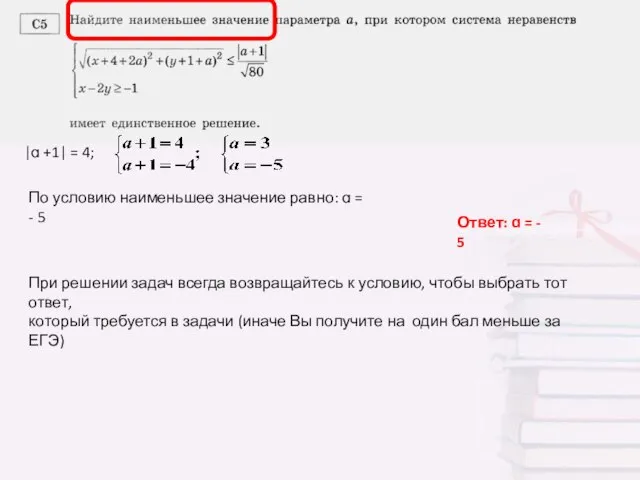
|ɑ +1| = 4;
По условию наименьшее значение равно: ɑ = - 5
Ответ: ɑ = - 5
При решении задач всегда возвращайтесь к условию, чтобы выбрать тот ответ,
который требуется в задачи (иначе Вы получите на один бал меньше за ЕГЭ)