СА practice

Приклад 1: Завдання протидії. Задані цільові функції супротивників, також множина стратегій кожного з них:
Далі ставитимемо завдання, які пропонується вирішити як контрольні, і вирішувати їх з докладними поясненнями.

1. Визначити гарантовані результати супротивників табличним методом, при цьому кроки сітки по стратегіях обох супротивників вважати рівними 1 (крок сітки вибраний великим в порівнянні з варіантами, що пропонується вирішити самостійно, але даний приклад носить показовий характер, при вирішенні контрольних завдань вказаний алгоритм треба буде програмувати).

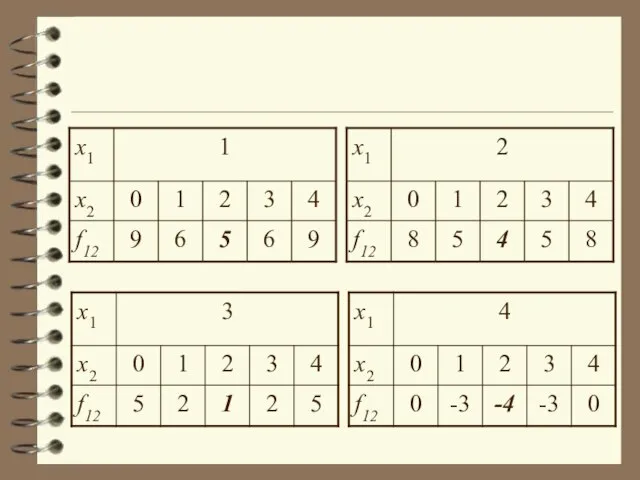
Рішення:
гарантований результат визначається за допомогою таблиць досить просто за принципом max min:
Для функції f12(x1,x2)

З таблиці видно, що

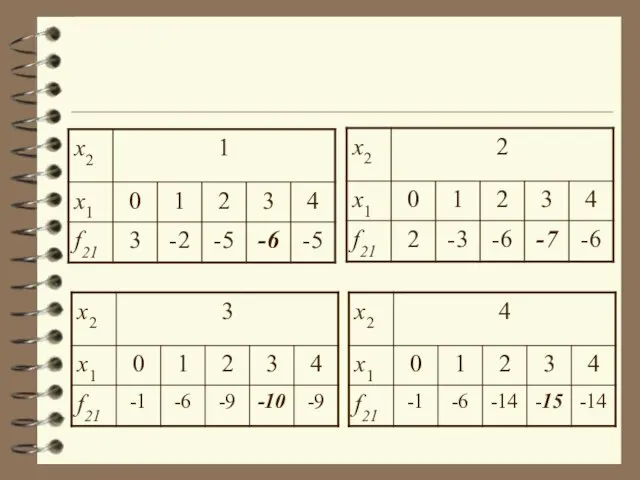
Знаходження гарантованого
результату f21*

З таблиці виходить, що
f21*=
Тепер визначимо гарантовані результати класичним методом, що базується на дослідженні екстремальних властивостей функцій.

Проведемо дослідження функції f12(x1,x2)
з даної умови отримуємо, що мінімум досягається при x2=2.
Тепер необхідно знайти значення x1, при якому наша функція досягатиме максимуму.

У f12(x1,x2) підставимо знайдене значення x2=2.
Візьмемо похідну по x1 і прирівняємо нулю:
звідки виходить, що x1 =1. З характеру функції знову виходить, що в крапці x1 =1 будет максимум

Отже, ми отримали, що
Те ж саме, але вже без пояснення виконаємо для другого гравця, тобто для функції f21 (x1,x2)

Отримаємо, що в крапці x1 =3 досягається мінімум
звідки витікає, що в крапці x2=1 досягається максимум. Отже

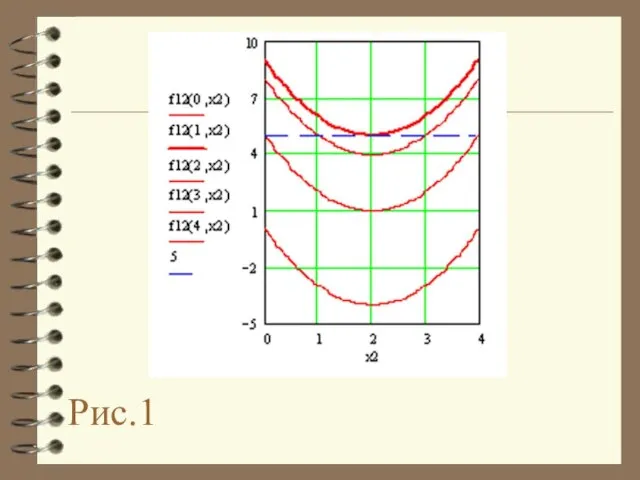
І, нарешті, для визначення f21*, f12*
скористаємося графічним методом.
Для знаходження f12*, фіксуючи ряд значень x1, будуються графіки функції f12(x1,x2) по x2 (рис.1).

Рис.1