Содержание
- 2. Приклад 1: Визначити множину Парето, якщо задані наступні цільові функції Порогові значення і обмеження задані:
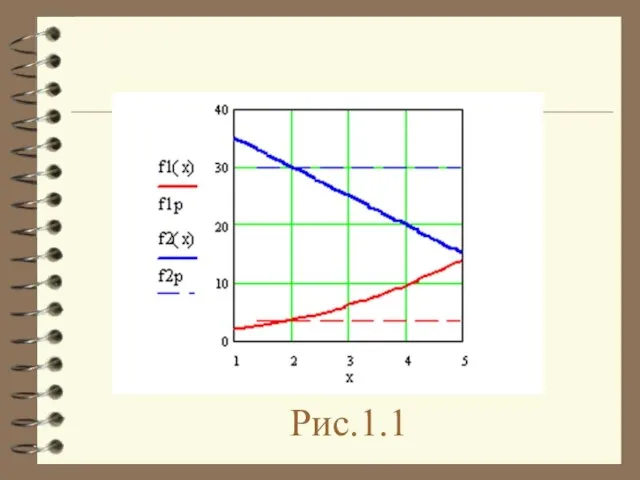
- 3. Рис.1.1
- 4. Задачу вирішуємо графічно, для чого будуємо графіки f1 i f2. З рис.1.1 видно, що для виконання
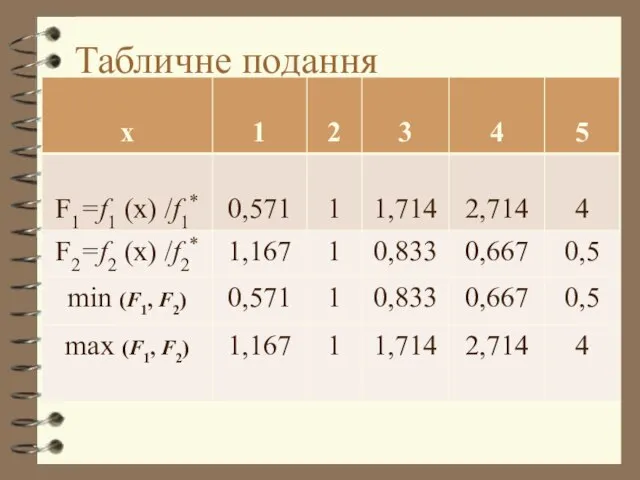
- 5. Табличне подання
- 6. З таблиці видно, що в крапці 2. В даному випадку ми просто звузили область [1; 5],
- 7. Звужена область - та, яка між стратегіями, що дають ці величини. Отже, розумно припустити, що множина
- 8. Приклад 2: Знайти область Парето і звузити її (хоч би з одного боку) якщо дано
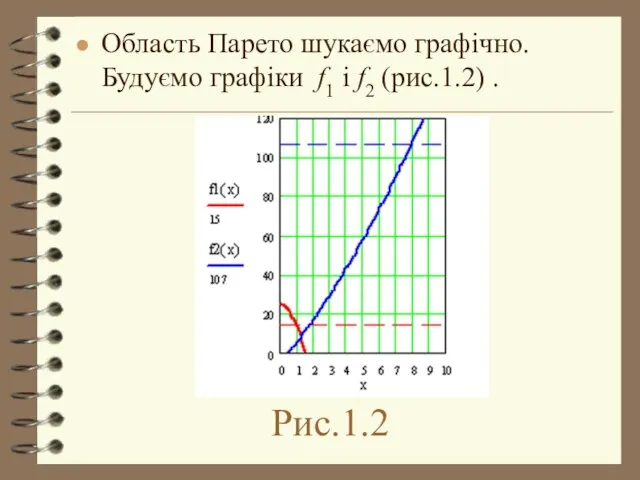
- 9. Рис.1.2 Область Парето шукаємо графічно. Будуємо графіки f1 i f2 (рис.1.2) .
- 10. а) Шукаємо область, що задовольняє нерівності для f1: б) Шукаємо область, що задовольняє нерівності для f2:
- 11. в) Загальну область шукаємо як перетин: [1;10] ∩ [0;8]=[1;8] , x ∈ [1;8] - область Парето,
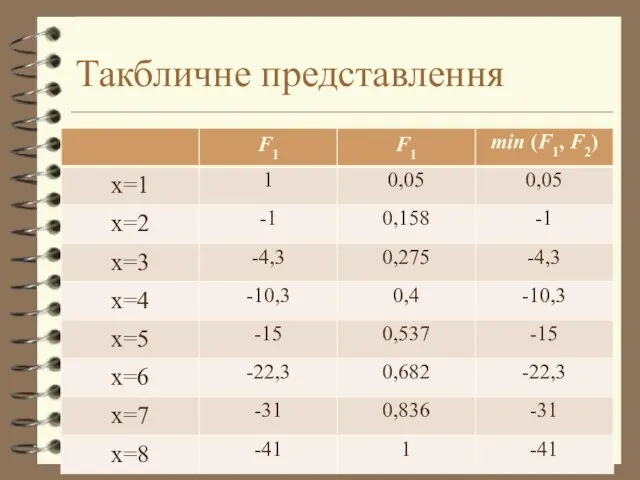
- 12. Такбличне представлення
- 13. Максимальним значенням з мінімальних є 0,05 . Наслідком цього є те, що відсікаємо всі x Оскільки
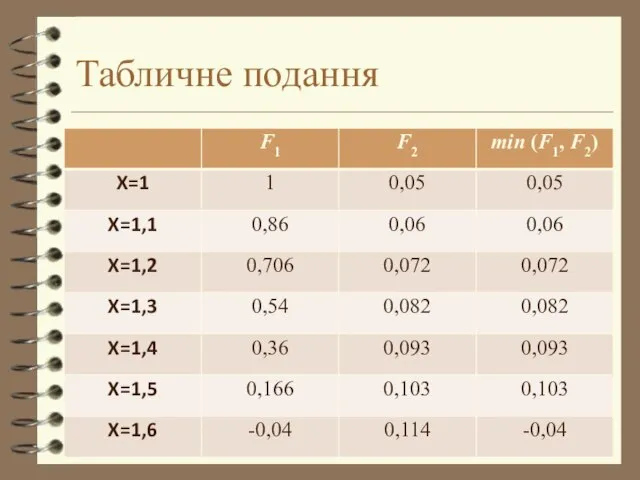
- 14. Табличне подання
- 15. Максимальним значенням з мінімальних є 0,103 . Наслідком цього є те, що відсікаємо усі x Тобто
- 16. Приклад 3 Для заданих цільових функцій, граничних обмежень і нерівностей знайти область Парето і звузити її.
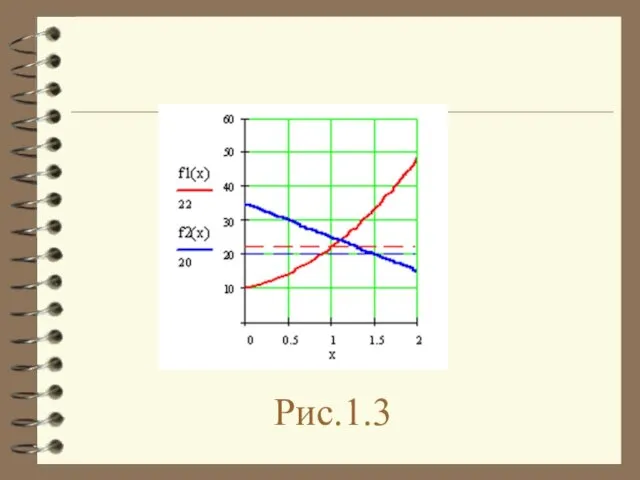
- 17. Рис.1.3
- 18. Шукаємо область Парето як множину, що задовольняє системі нерівностей: Аналітичне вирішення системи нерівностей: х є [1;1,5].
- 19. Табличне подання
- 20. З таблиці видно, що в точці х=1.2. Згідно теорії звужена область Парето лежить між крапками, в
- 22. Скачать презентацию






![в) Загальну область шукаємо як перетин: [1;10] ∩ [0;8]=[1;8] , x ∈](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/382509/slide-10.jpg)






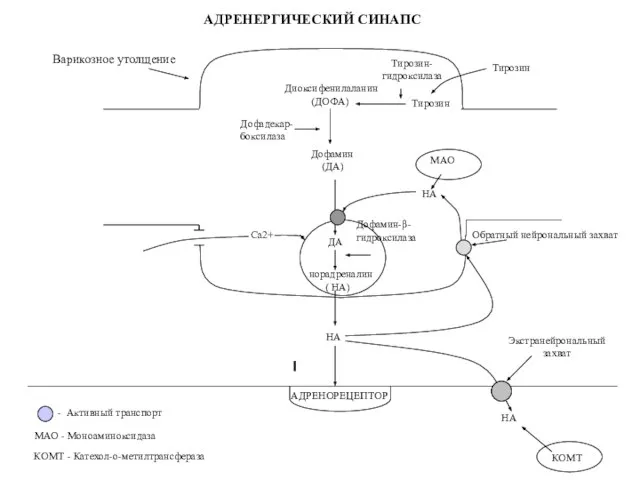 Адреномиметики
Адреномиметики Sport in Canada
Sport in Canada АО Вюрт Северо-Запад, Санкт-Петербург. Боулинг–турнир. Месяц новых клиентов
АО Вюрт Северо-Запад, Санкт-Петербург. Боулинг–турнир. Месяц новых клиентов Презентация на тему Русский герой сказок: Иван-дурак
Презентация на тему Русский герой сказок: Иван-дурак  Путешествие на водопад Атыш
Путешествие на водопад Атыш Помада Creamy Glam
Помада Creamy Glam Презентация по английскому Королевская семья Великобритании
Презентация по английскому Королевская семья Великобритании tema-gribi-rodnaya-tropinka_ru
tema-gribi-rodnaya-tropinka_ru Работа социального педагога с детьми имеющих отклоняющее поведение.
Работа социального педагога с детьми имеющих отклоняющее поведение. Комплекс упражнений утренней гимнастики
Комплекс упражнений утренней гимнастики Службы для электронного общения
Службы для электронного общения Характер и темперамент
Характер и темперамент Обществознание
Обществознание Материально-техническая база одно из условий эффективной реализации профильного обучения.
Материально-техническая база одно из условий эффективной реализации профильного обучения. Способ тепловой обработки сыпучих материалов и устройства для его осуществления
Способ тепловой обработки сыпучих материалов и устройства для его осуществления Архитектура Санкт-Петербурга
Архитектура Санкт-Петербурга project
project Greenway. Жизнь без химии с заботой о семье и природе
Greenway. Жизнь без химии с заботой о семье и природе Адрес: Тверская область, г. Нелидово Ул. Шахтерская 16
Адрес: Тверская область, г. Нелидово Ул. Шахтерская 16 Сказочные птицы
Сказочные птицы Леонардо Да Винчи
Леонардо Да Винчи Как преодолеть стресс перед экзаменом
Как преодолеть стресс перед экзаменом Признаки нарушения адаптации в почерке
Признаки нарушения адаптации в почерке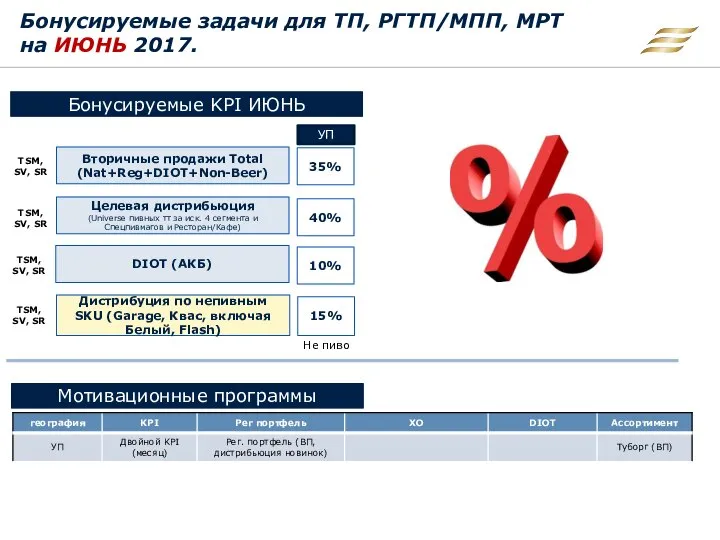 Бонусируемые задачи для ТП, РГТП/МПП, МРТ на июнь 2017
Бонусируемые задачи для ТП, РГТП/МПП, МРТ на июнь 2017 Доходы предприятия и финансовые результаты его деятельности
Доходы предприятия и финансовые результаты его деятельности Алтайский государственный университет
Алтайский государственный университет Методика оформление. Пушкинская карта
Методика оформление. Пушкинская карта Презентация на тему Социальная информатика
Презентация на тему Социальная информатика