Содержание
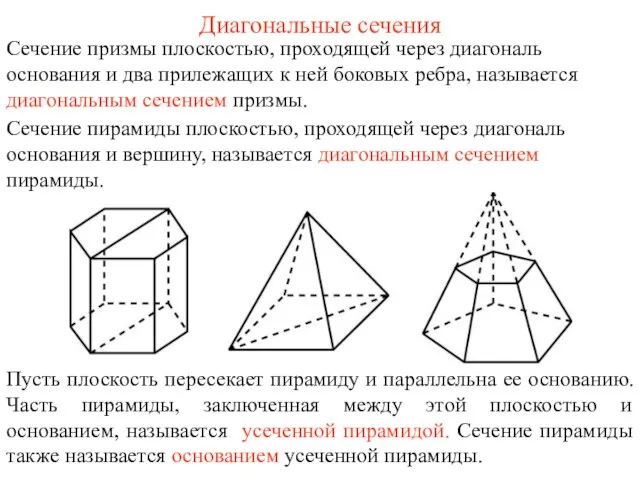
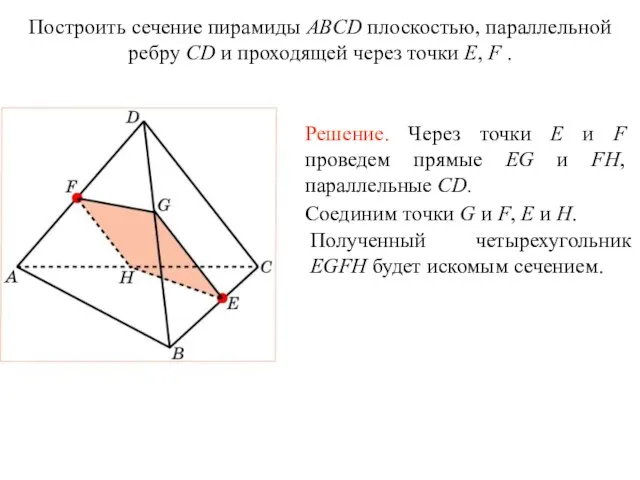
- 2. Сечение призмы плоскостью, проходящей через диагональ основания и два прилежащих к ней боковых ребра, называется диагональным
- 3. Какой фигурой может быть сечение многогранника плоскостью? Упражнение 1 Ответ: Многоугольником или объединением нескольких многоугольников.
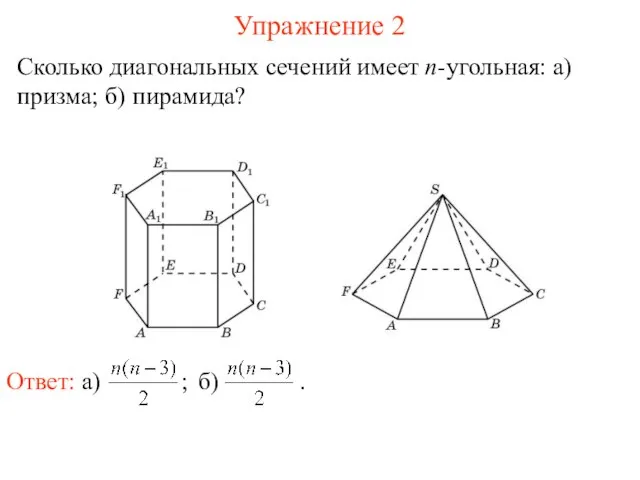
- 4. Сколько диагональных сечений имеет n-угольная: а) призма; б) пирамида? Упражнение 2
- 5. Может ли в сечении куба плоскостью получиться: а) треугольник? Упражнение 3 Ответ: а) Да; б) правильный
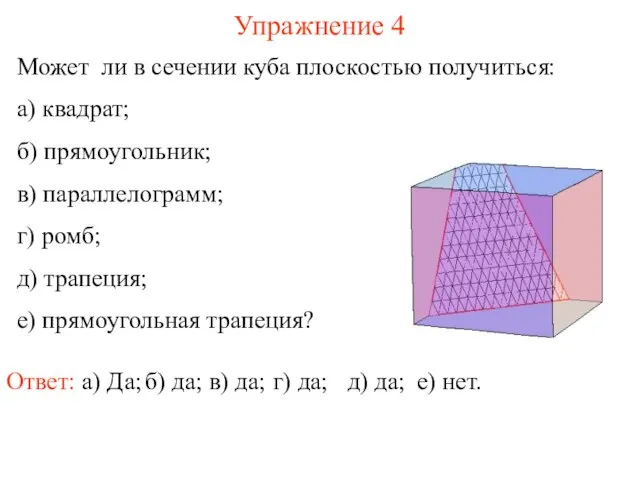
- 6. Может ли в сечении куба плоскостью получиться: а) квадрат; б) прямоугольник; в) параллелограмм; г) ромб; д)
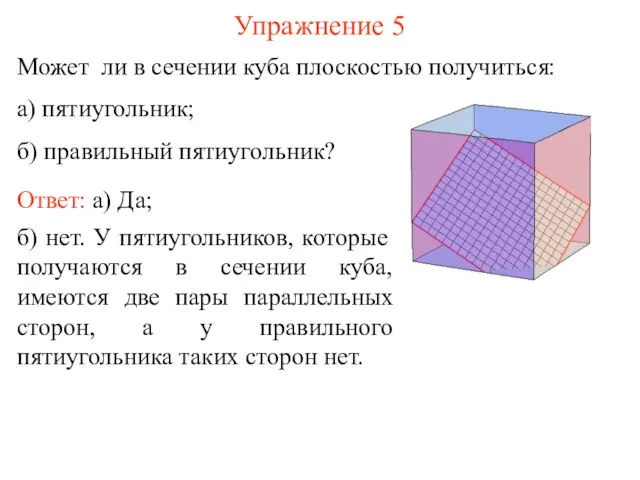
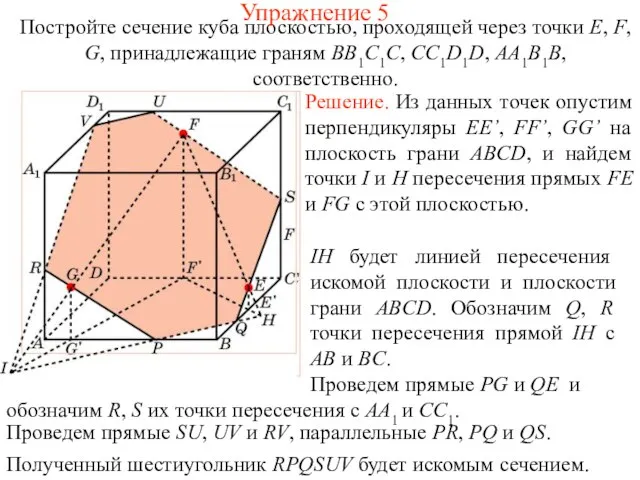
- 7. Может ли в сечении куба плоскостью получиться: а) пятиугольник; б) правильный пятиугольник? Упражнение 5 б) нет.
- 8. Может ли в сечении куба плоскостью получиться: а) шестиугольник; б) правильный шестиугольник; в) многоугольник с числом
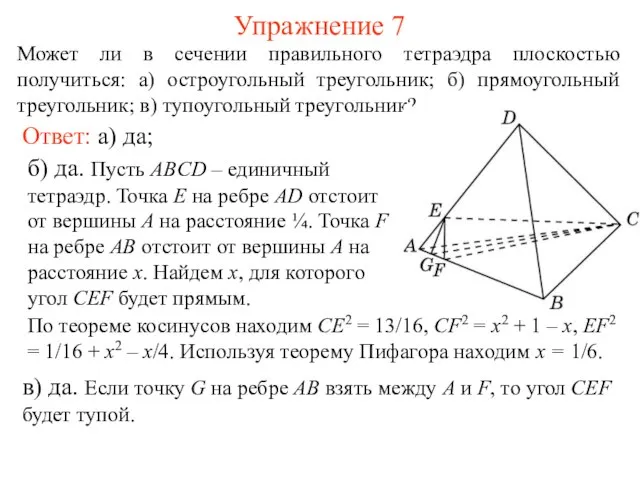
- 9. Может ли в сечении правильного тетраэдра плоскостью получиться: а) остроугольный треугольник; б) прямоугольный треугольник; в) тупоугольный
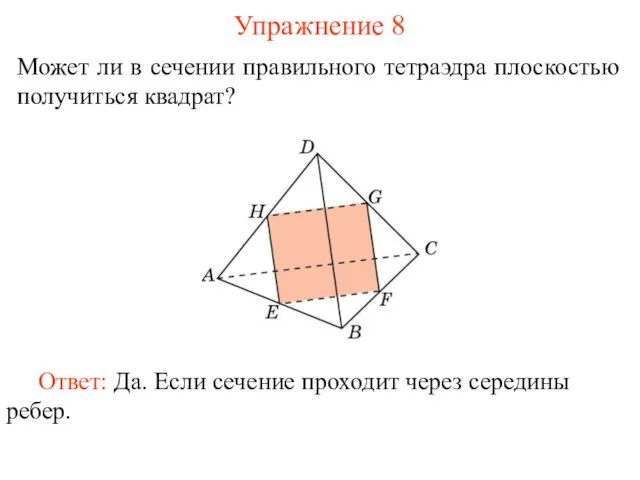
- 10. Может ли в сечении правильного тетраэдра плоскостью получиться квадрат? Упражнение 8
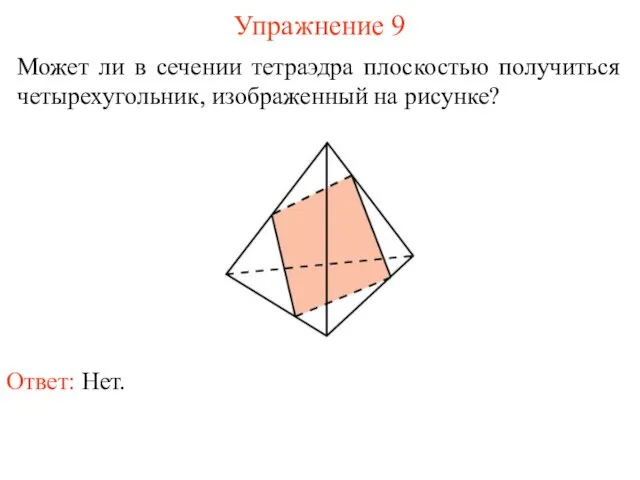
- 11. Может ли в сечении тетраэдра плоскостью получиться четырехугольник, изображенный на рисунке? Упражнение 9 Ответ: Нет.
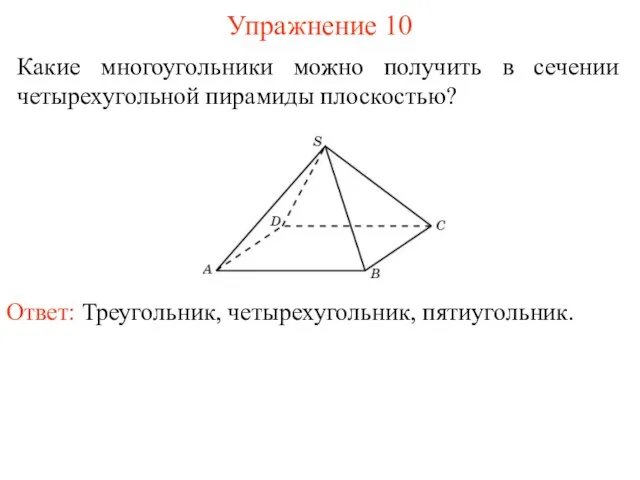
- 12. Какие многоугольники можно получить в сечении четырехугольной пирамиды плоскостью? Упражнение 10 Ответ: Треугольник, четырехугольник, пятиугольник.
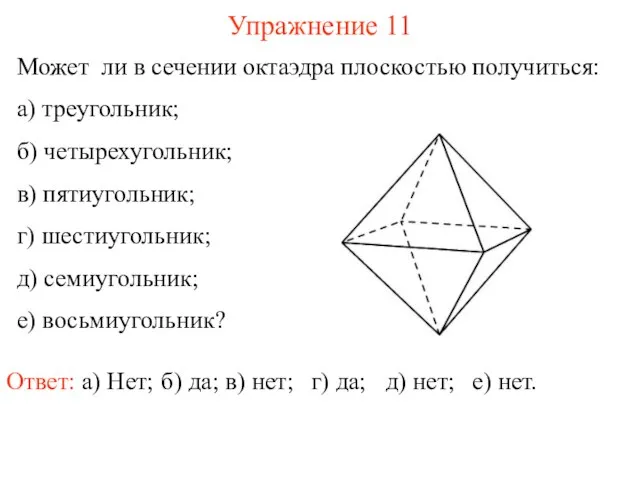
- 13. Может ли в сечении октаэдра плоскостью получиться: а) треугольник; б) четырехугольник; в) пятиугольник; г) шестиугольник; д)
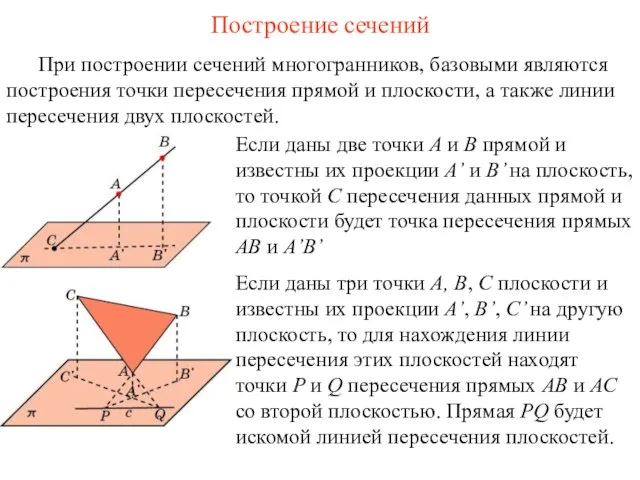
- 14. При построении сечений многогранников, базовыми являются построения точки пересечения прямой и плоскости, а также линии пересечения
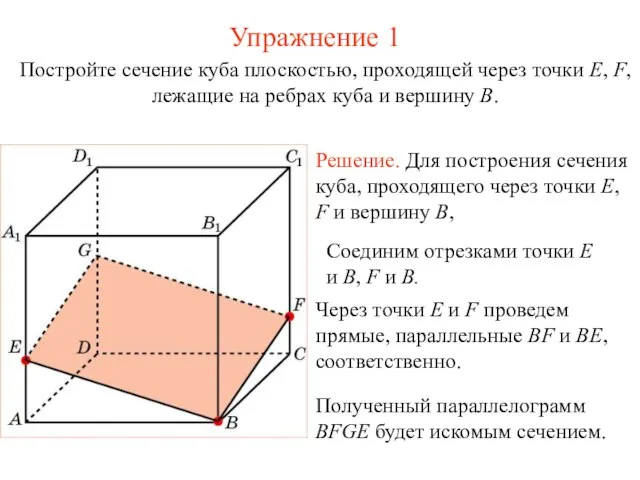
- 15. Решение. Для построения сечения куба, проходящего через точки E, F и вершину B, Упражнение 1
- 16. Решение. Для построения сечения куба, проходящего через точки E, F, G, проведем прямую EF и обозначим
- 17. Решение. Для построения сечения куба, проходящего через точки E, F, G, проведем прямую EF и обозначим
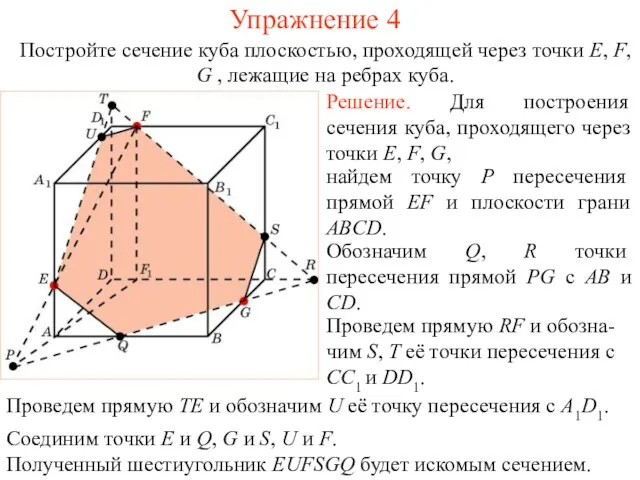
- 18. Решение. Для построения сечения куба, проходящего через точки E, F, G, найдем точку P пересечения прямой
- 19. Упражнение 5
- 20. Упражнение 6
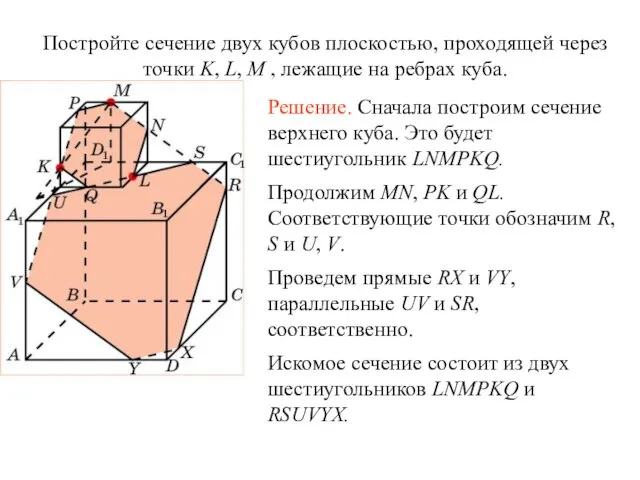
- 21. Постройте сечение двух кубов плоскостью, проходящей через точки K, L, M , лежащие на ребрах куба.
- 22. Упражнение 8
- 23. Упражнение 9
- 24. Постройте сечение призмы ABCA1B1C1 плоскостью, параллельной AC1, проходящей через точки D и D1. Упражнение 10
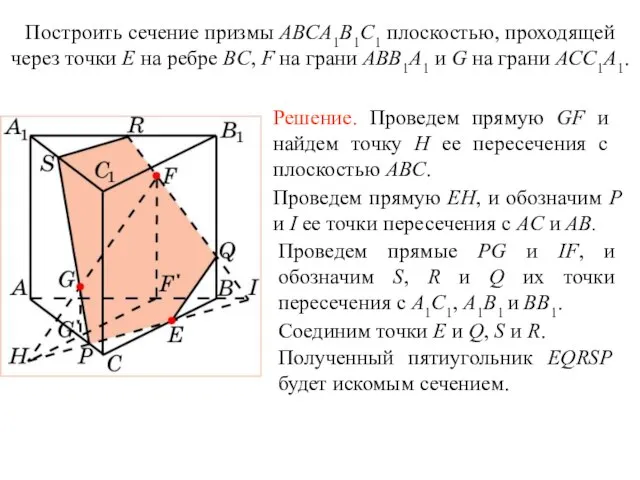
- 25. Упражнение 11
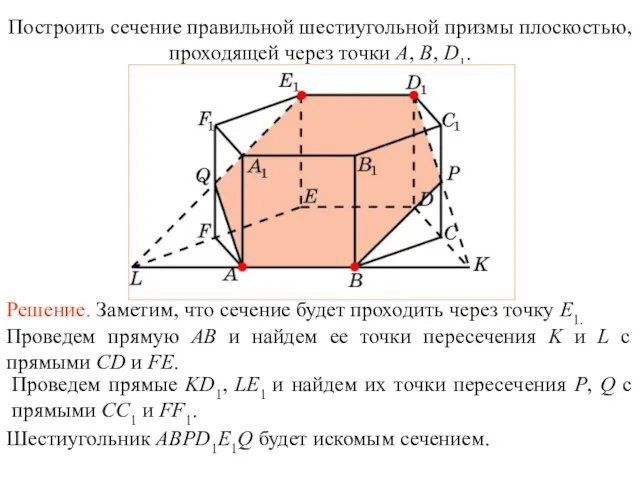
- 26. Построить сечение правильной шестиугольной призмы плоскостью, проходящей через точки A, B, D1. Упражнение 12
- 27. Упражнение 13
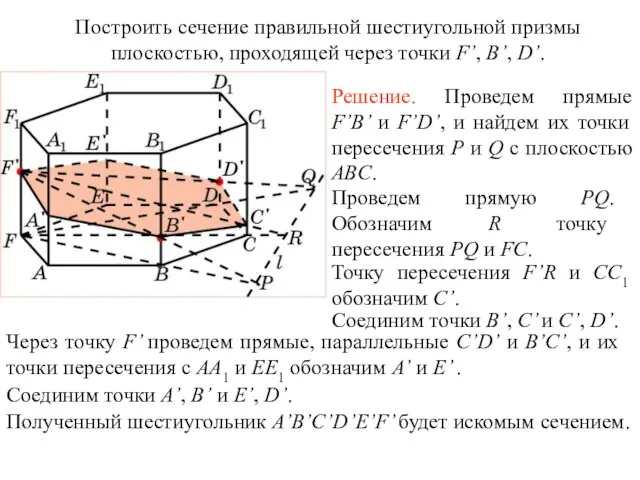
- 28. Построить сечение правильной шестиугольной призмы плоскостью, проходящей через точки F’, B’, D’. Упражнение 14
- 29. Упражнение 15
- 30. Упражнение 16
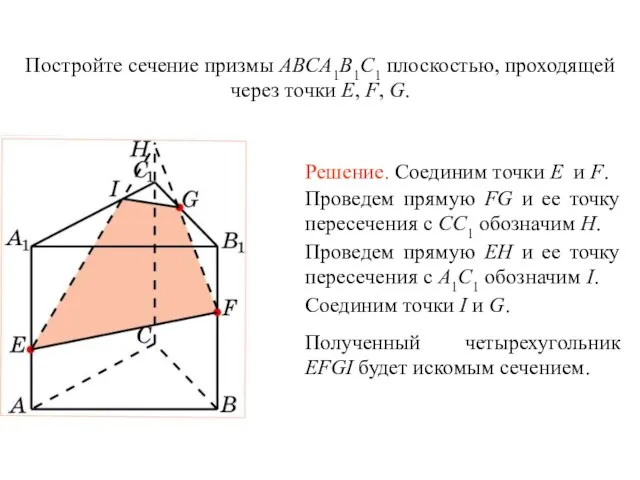
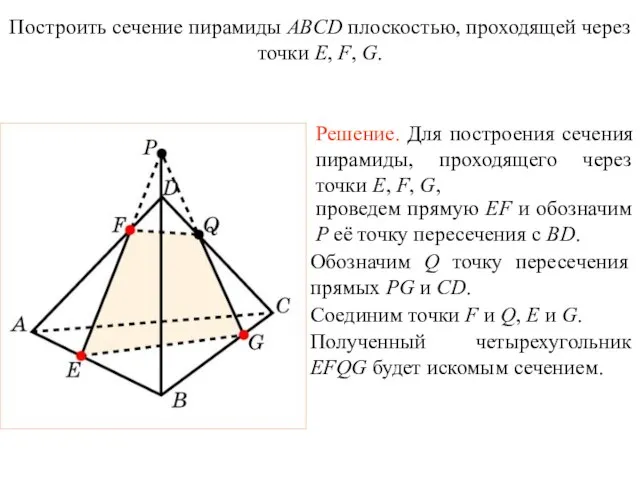
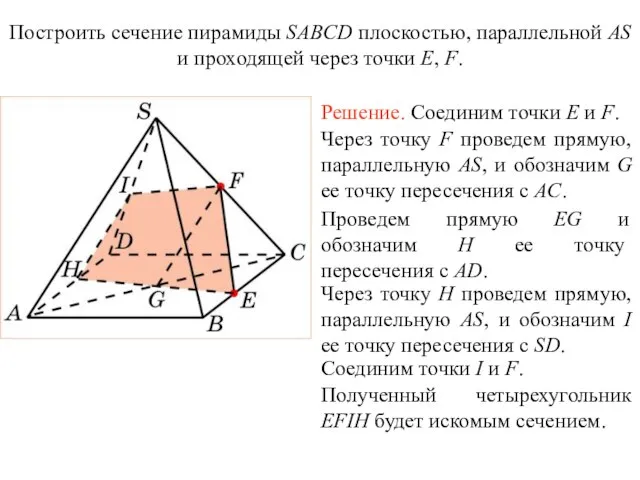
- 31. Решение. Для построения сечения пирамиды, проходящего через точки E, F, G, проведем прямую EF и обозначим
- 32. Упражнение 18
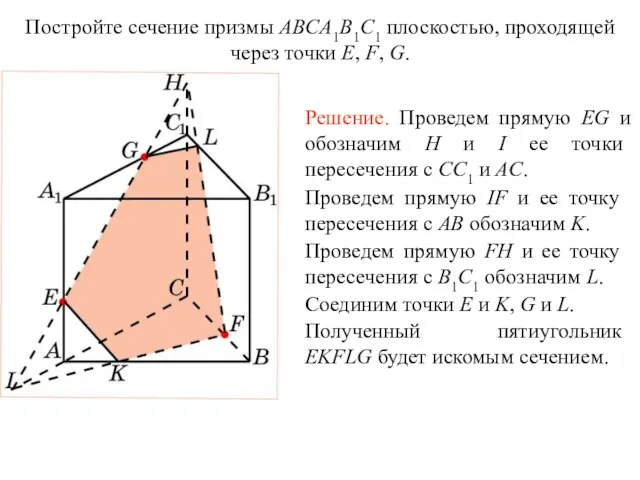
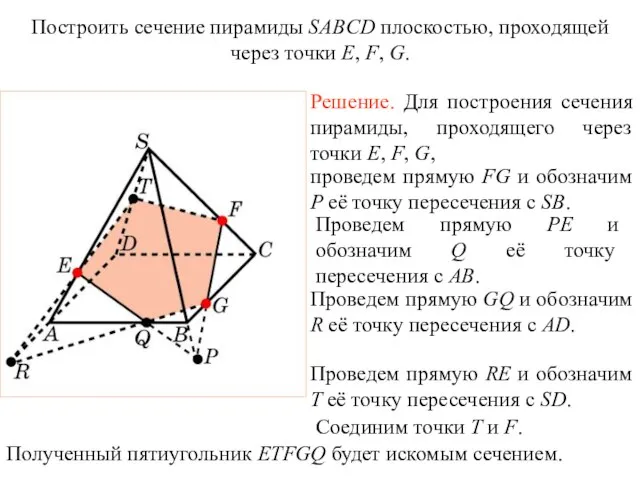
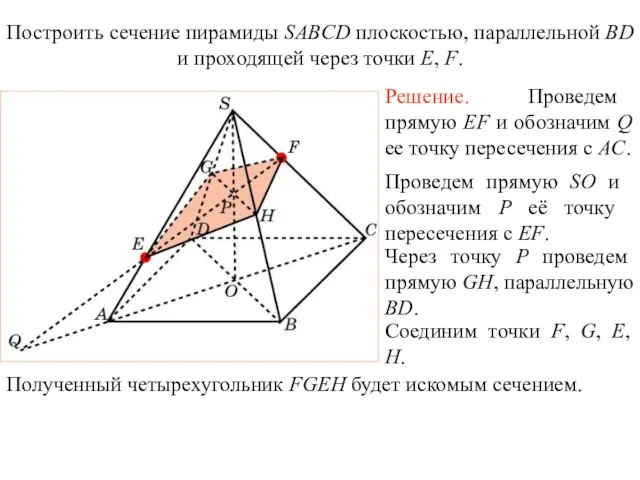
- 33. Решение. Для построения сечения пирамиды, проходящего через точки E, F, G, проведем прямую FG и обозначим
- 34. Упражнение 20
- 35. Упражнение 21
- 37. Скачать презентацию








 Законодательство Республики Казахстан в области информационной безопасности
Законодательство Республики Казахстан в области информационной безопасности Духи
Духи Обобщение темы«Тепловые явления»
Обобщение темы«Тепловые явления» Каникулы
Каникулы Родительское собрание
Родительское собрание П рофильное обучение в старших классах, ориентированно на индивидуализацию обучения и социализацию обучающихся (с учетом реальны
П рофильное обучение в старших классах, ориентированно на индивидуализацию обучения и социализацию обучающихся (с учетом реальны Зима в парке
Зима в парке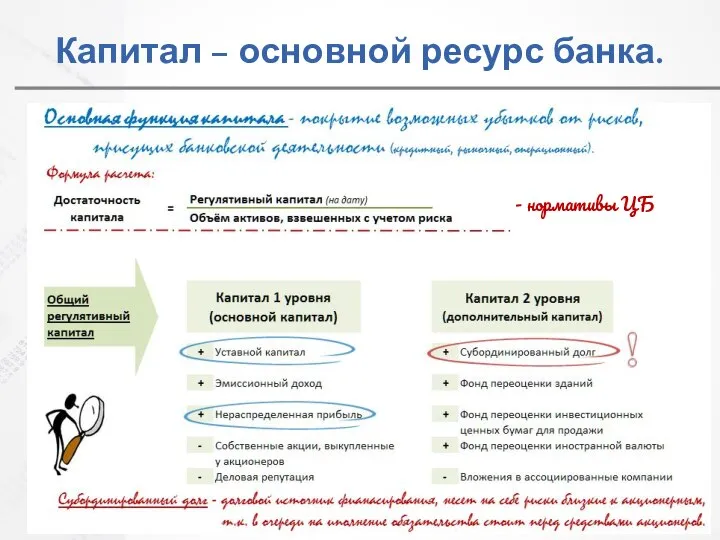 Капитал - основной ресурс банка. Формулы
Капитал - основной ресурс банка. Формулы Hyundai Sonata2.7V6сравнение с конкурентами
Hyundai Sonata2.7V6сравнение с конкурентами Кристаллические тела 10 класс
Кристаллические тела 10 класс Глава №9. Международные сопоставления ВВП и его компонентов на основе паритетов покупательской способности валют
Глава №9. Международные сопоставления ВВП и его компонентов на основе паритетов покупательской способности валют Презентация на тему Каменный уголь
Презентация на тему Каменный уголь  РАЗВИТИЕ ТЕХНОЛОГИЙ ПРОВЕДЕНИЯ МЕЖРЕГИОНАЛЬНЫХ СДЕЛОК
РАЗВИТИЕ ТЕХНОЛОГИЙ ПРОВЕДЕНИЯ МЕЖРЕГИОНАЛЬНЫХ СДЕЛОК Выколотка. Чеканка. Гравировка
Выколотка. Чеканка. Гравировка Презентация на тему «История создания Linux»
Презентация на тему «История создания Linux» Презентация на тему Лес наш друг
Презентация на тему Лес наш друг  Презентация на тему Русско-японская война 1904-1905 гг
Презентация на тему Русско-японская война 1904-1905 гг  Презентация на тему Английские колонии в Северной Америке 7 класс
Презентация на тему Английские колонии в Северной Америке 7 класс Мãн Хураçкари пĕтемĕшле пĕлӳ паракан тĕп шкул
Мãн Хураçкари пĕтемĕшле пĕлӳ паракан тĕп шкул Презентация на тему Famous British Writers (Знаменитые британские писатели)
Презентация на тему Famous British Writers (Знаменитые британские писатели)  ЗАБЕЗПЕЧЕННЯ ДОСТУПУ ДО ПУБЛІЧНОI ІНФОРМАЦІI
ЗАБЕЗПЕЧЕННЯ ДОСТУПУ ДО ПУБЛІЧНОI ІНФОРМАЦІI Црква у хришћанској архитектури
Црква у хришћанској архитектури Природные зоны. Лес. Растения леса
Природные зоны. Лес. Растения леса Краткое описание ресурса Одни из немногих футбольных интернет ресурсов на территории Украины, который подает информацию на 2-х язы
Краткое описание ресурса Одни из немногих футбольных интернет ресурсов на территории Украины, который подает информацию на 2-х язы My favourite city. Шаблон
My favourite city. Шаблон Презентация на тему Литература Древней Руси
Презентация на тему Литература Древней Руси urok-povtoreniya-po-kursu-obschestvoznaniya-dlya-7
urok-povtoreniya-po-kursu-obschestvoznaniya-dlya-7 Современное искусство Египта
Современное искусство Египта