Сечение поверхности

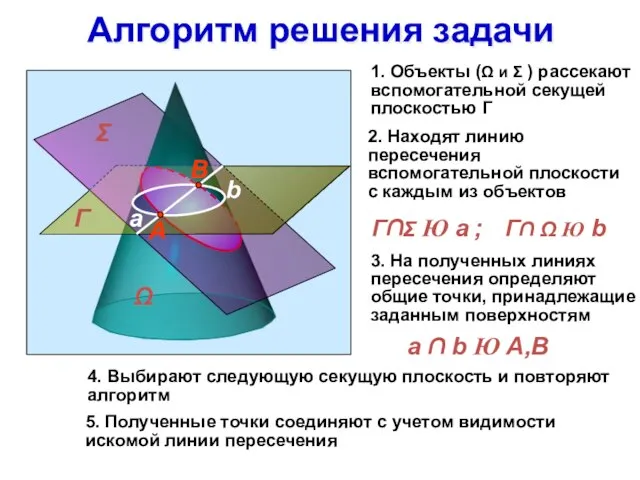
Алгоритм решения задачи
1. Объекты ( и  ) рассекают вспомогательной секущей плоскостью Г
2. Находят линию пересечения вспомогательной плоскости с каждым из объектов
4. Выбирают следующую секущую плоскость и повторяют алгоритм
5. Полученные точки соединяют с учетом видимости искомой линии пересечения
a  b Ю A,B
3. На полученных линиях пересечения определяют общие точки, принадлежащие заданным поверхностям



Методические указания
Плоскость, пересекающая поверхность, может занимать общее и частное положение относительно плоскостей проекций
В общем случае вид сечения – кривая линия
Сечение поверхности вращения плоскостью является фигурой симметричной. Ось симметрии фигуры сечения лежит в плоскости общей симметрии заданной поверхности и плоскости, при условии:
- проходит через ось вращения поверхности;
- перпендикулярности секущей плоскости
Сечением многогранной поверхности является ломаная линия, вершины которой лежат на ребрах поверхности

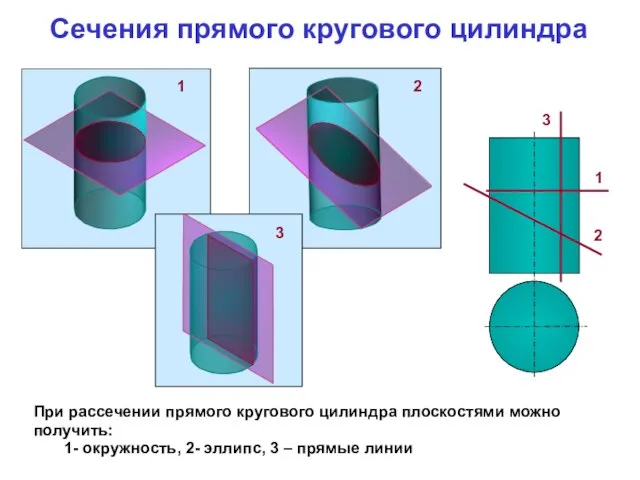
При рассечении прямого кругового цилиндра плоскостями можно получить:
1- окружность, 2- эллипс, 3 – прямые линии
Сечения прямого кругового цилиндра

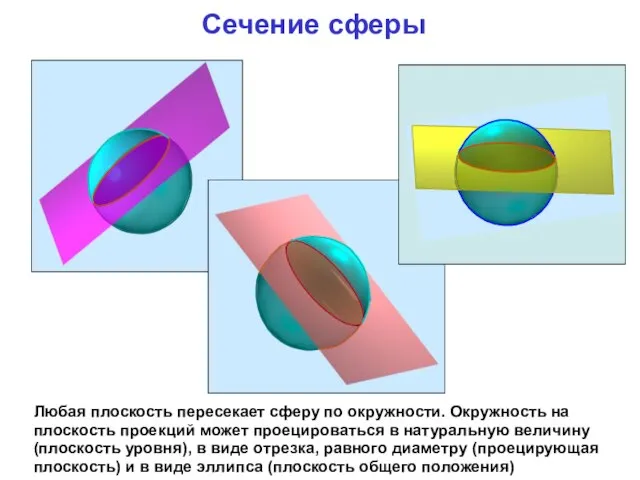
Сечение сферы
Любая плоскость пересекает сферу по окружности. Окружность на плоскость проекций может проецироваться в натуральную величину (плоскость уровня), в виде отрезка, равного диаметру (проецирующая плоскость) и в виде эллипса (плоскость общего положения)

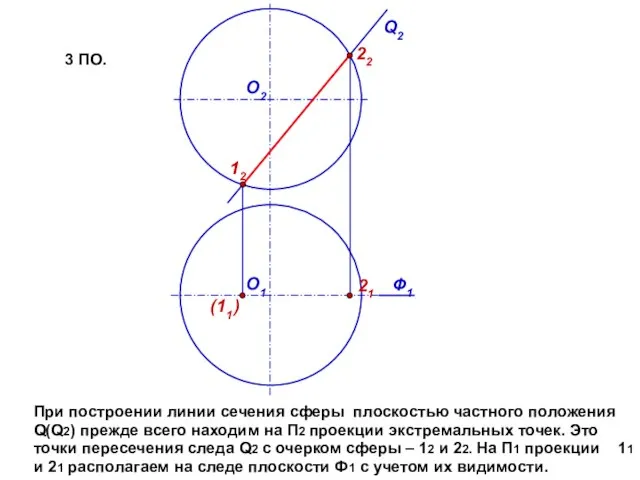
Q2
О1
О2
При построении линии сечения сферы плоскостью частного положения Q(Q2) прежде всего находим на П2 проекции экстремальных точек. Это точки пересечения следа Q2 с очерком сферы – 12 и 22. На П1 проекции 11 и 21 располагаем на следе плоскости Ф1 с учетом их видимости.
3 ПО.

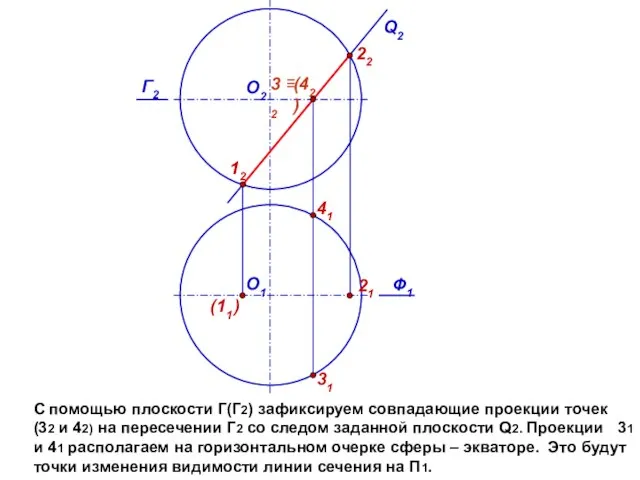
С помощью плоскости Г(Г2) зафиксируем совпадающие проекции точек (32 и 42) на пересечении Г2 со следом заданной плоскости Q2. Проекции 31 и 41 располагаем на горизонтальном очерке сферы – экваторе. Это будут точки изменения видимости линии сечения на П1.
Q2
О1
О2

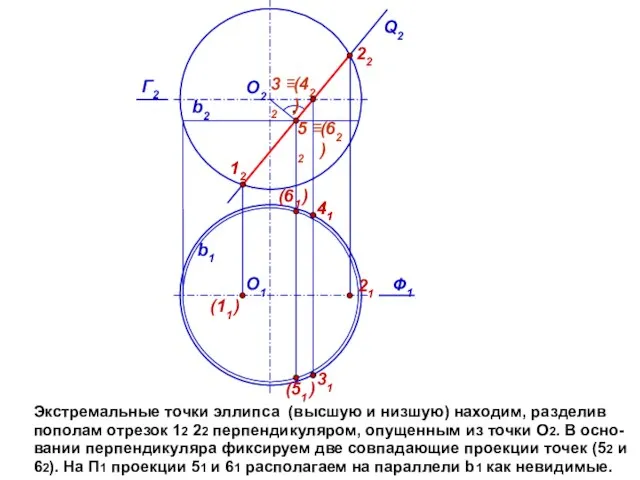
Экстремальные точки эллипса (высшую и низшую) находим, разделив пополам отрезок 12 22 перпендикуляром, опущенным из точки О2. В осно- вании перпендикуляра фиксируем две совпадающие проекции точек (52 и 62). На П1 проекции 51 и 61 располагаем на параллели b1 как невидимые.
Q2
О1
О2
(11 )
21

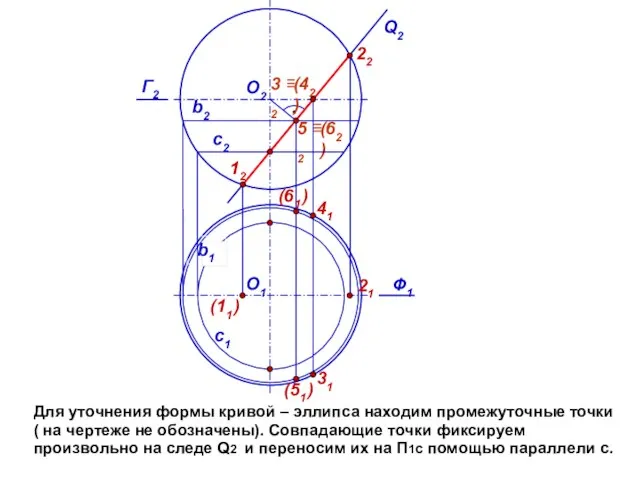
Для уточнения формы кривой – эллипса находим промежуточные точки
( на чертеже не обозначены). Совпадающие точки фиксируем произвольно на следе Q2 и переносим их на П1с помощью параллели с.
Q2
О2
(11 )
(61 )
21
b2
(51 )
О1

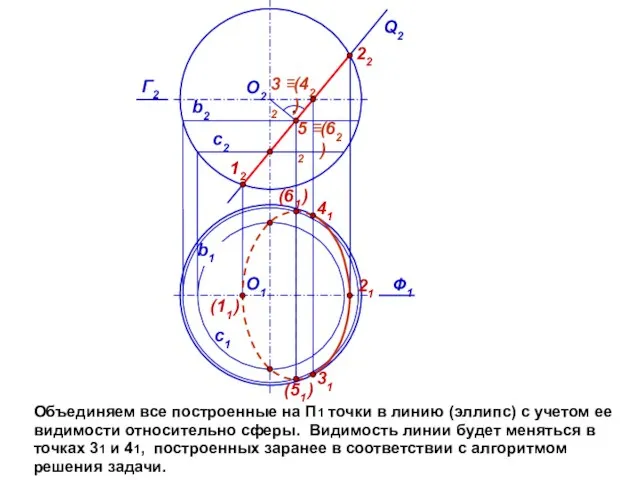
Объединяем все построенные на П1 точки в линию (эллипс) с учетом ее видимости относительно сферы. Видимость линии будет меняться в точках 31 и 41, построенных заранее в соответствии с алгоритмом решения задачи.
Q2
с1
О2
(11 )
(61 )
21
b2
(51 )
с2
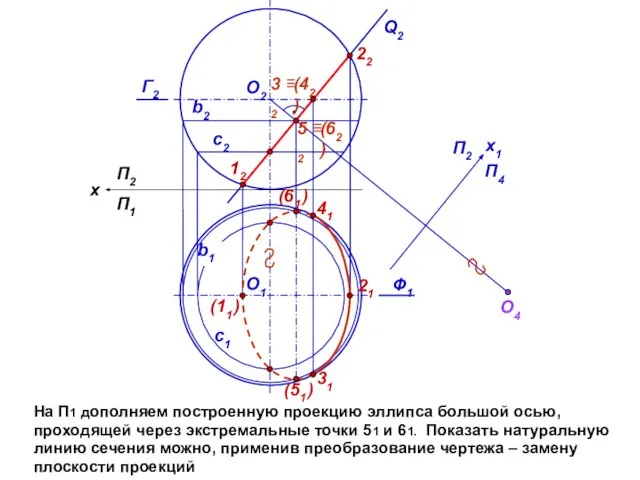
О1

На П1 дополняем построенную проекцию эллипса большой осью, проходящей через экстремальные точки 51 и 61. Показать натуральную линию сечения можно, применив преобразование чертежа – замену плоскости проекций
Q2
с1
О2
(11 )
(61 )
21
b2
(51 )
с2
О1

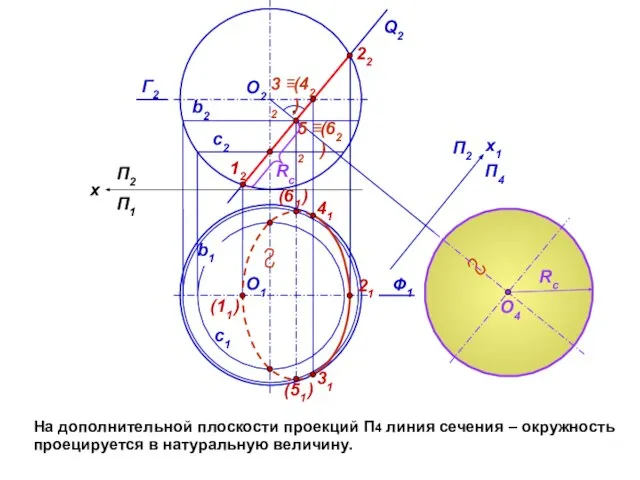
На дополнительной плоскости проекций П4 линия сечения – окружность проецируется в натуральную величину.
Q2
с1
О2
(11 )
(61 )
21
b2
(51 )
с2
О1
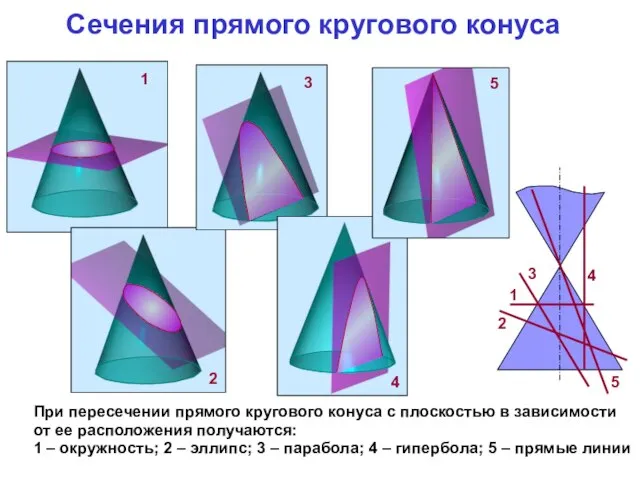
О4

Сечения прямого кругового конуса
При пересечении прямого кругового конуса с плоскостью в зависимости от ее расположения получаются:
1 – окружность; 2 – эллипс; 3 – парабола; 4 – гипербола; 5 – прямые линии

В сечении конической поверхности вращения плоскостью могут быть получены различные геометрические образы
В плоскости Г – точка,
Δ – окружность,
Θ – эллипс,
Σ – гипербола,
Ф – парабола,
Ψ – одна прямая,
Ω – две прямые.

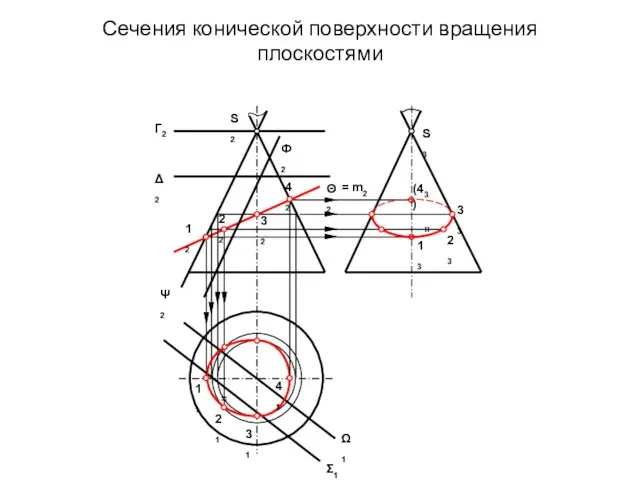
Сечения конической поверхности вращения плоскостями
S3
S2
Г2
Δ2
Ф2
2
Ψ2
Σ1
Ω1
S1
= m2

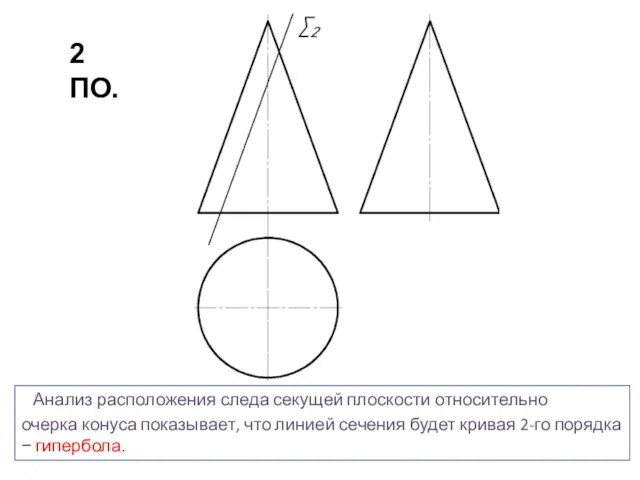
Анализ расположения следа секущей плоскости относительно
очерка конуса показывает, что линией сечения будет кривая 2-го порядка  гипербола.
2 ПО.

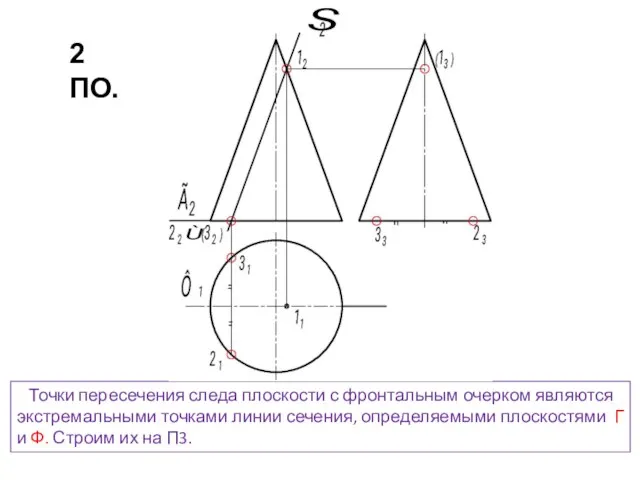
Точки пересечения следа плоскости с фронтальным очерком являются экстремальными точками линии сечения, определяемыми плоскостями Г и Ф. Строим их на П3.
2 ПО.

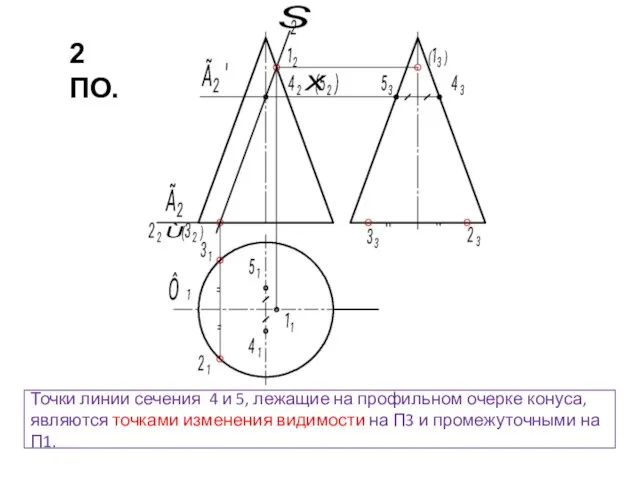
Точки линии сечения 4 и 5, лежащие на профильном очерке конуса, являются точками изменения видимости на П3 и промежуточными на П1.
2 ПО.

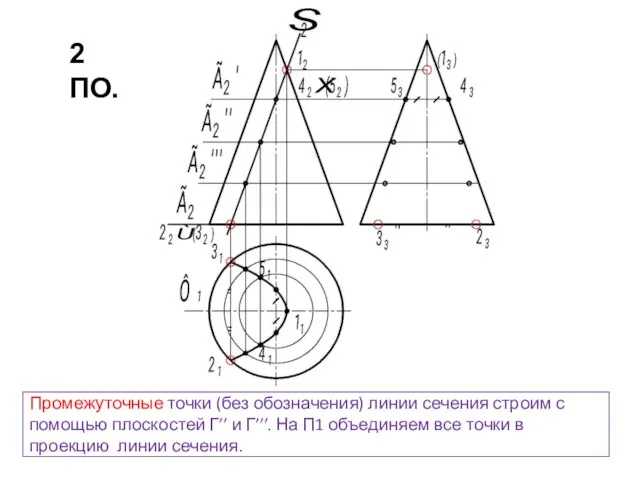
Промежуточные точки (без обозначения) линии сечения строим с помощью плоскостей Г’’ и Г’’’. На П1 объединяем все точки в проекцию линии сечения.
2 ПО.