Содержание
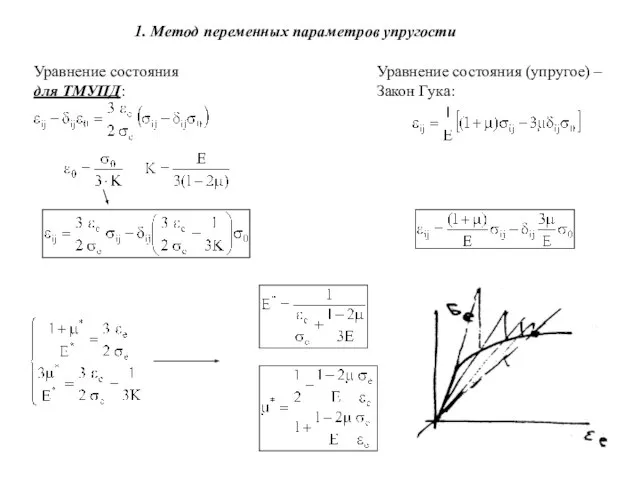
- 2. 1. Метод переменных параметров упругости Уравнение состояния для ТМУПД: Уравнение состояния (упругое) – Закон Гука:
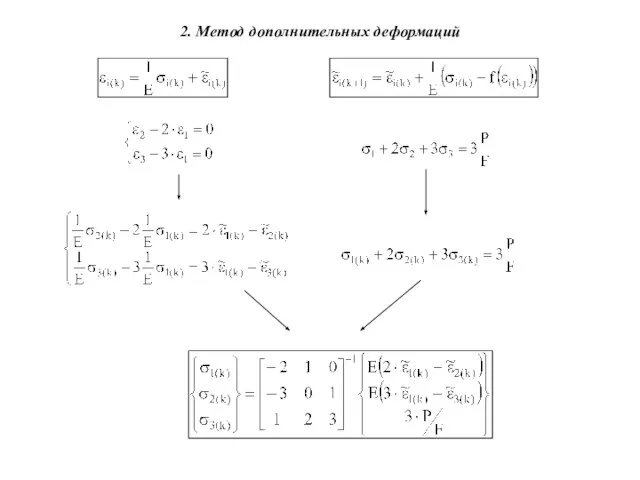
- 3. 2. Метод дополнительных деформаций вектор дополнительных деформаций закон течения упругие деформации для ТМУПД: упругий закон
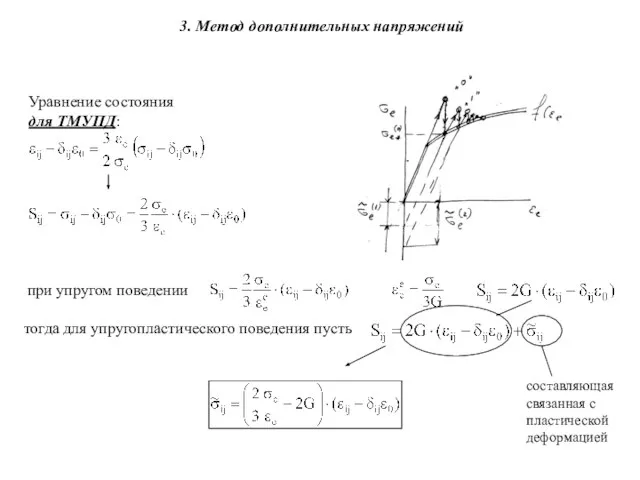
- 4. 3. Метод дополнительных напряжений Уравнение состояния для ТМУПД: при упругом поведении тогда для упругопластического поведения пусть
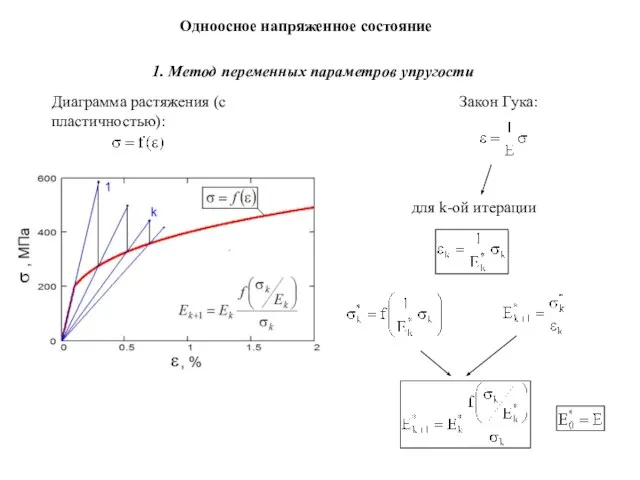
- 5. Одноосное напряженное состояние 1. Метод переменных параметров упругости Диаграмма растяжения (с пластичностью): Закон Гука: для k-ой
- 6. 2. Метод дополнительных деформаций вектор дополнительных деформаций диаграмма растяжения упругие деформации Одноосное напряженное состояние
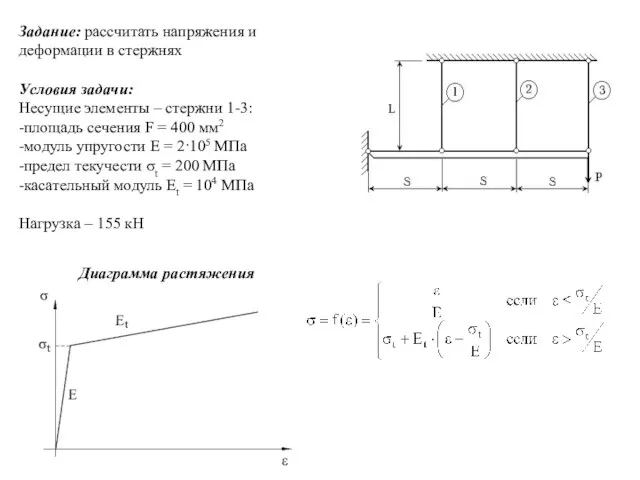
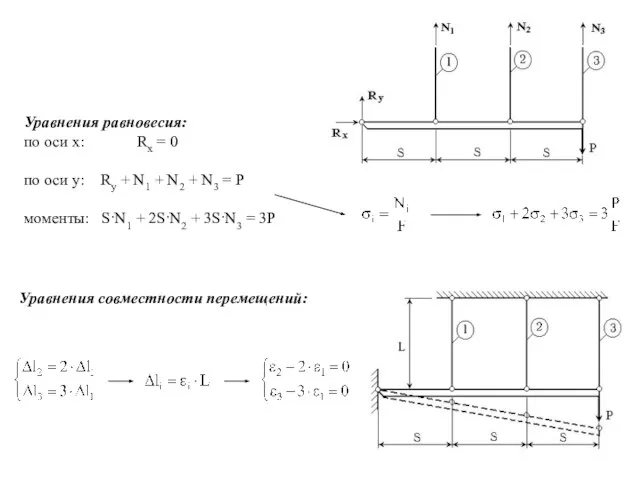
- 7. Задание: рассчитать напряжения и деформации в стержнях Условия задачи: Несущие элементы – стержни 1-3: -площадь сечения
- 8. Уравнения совместности перемещений: Уравнения равновесия: по оси х: Rx = 0 по оси y: Ry +
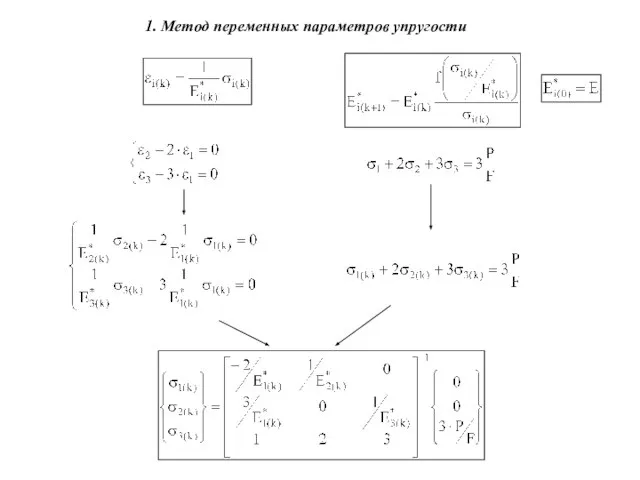
- 9. 1. Метод переменных параметров упругости
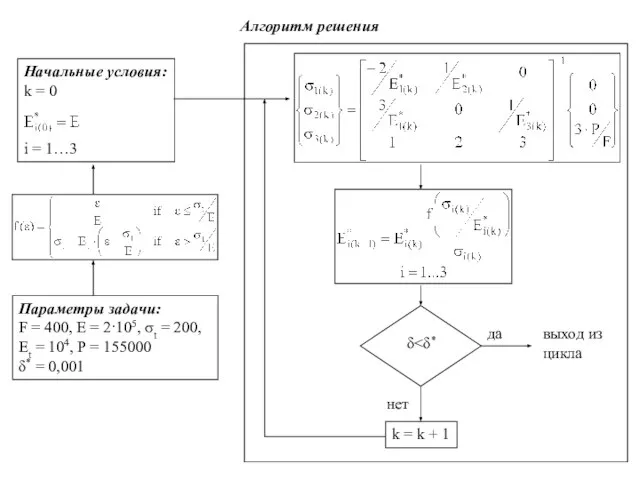
- 10. Начальные условия: k = 0 i = 1…3 Параметры задачи: F = 400, E = 2·105,
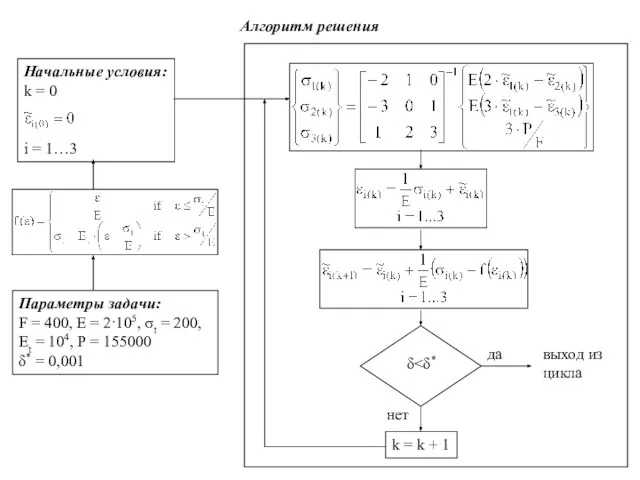
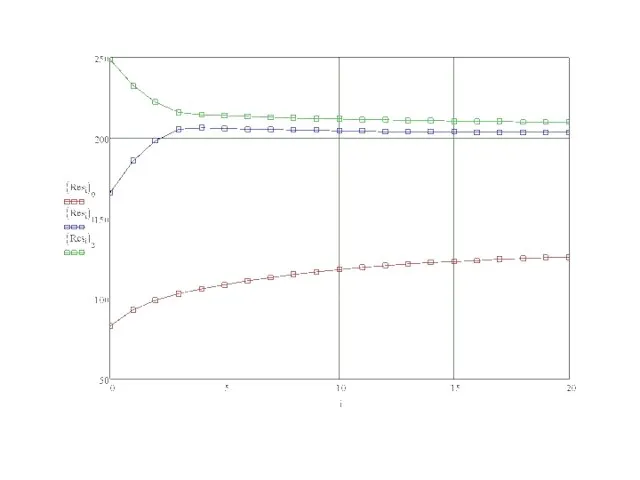
- 12. 2. Метод дополнительных деформаций
- 13. Начальные условия: k = 0 i = 1…3 Параметры задачи: F = 400, E = 2·105,
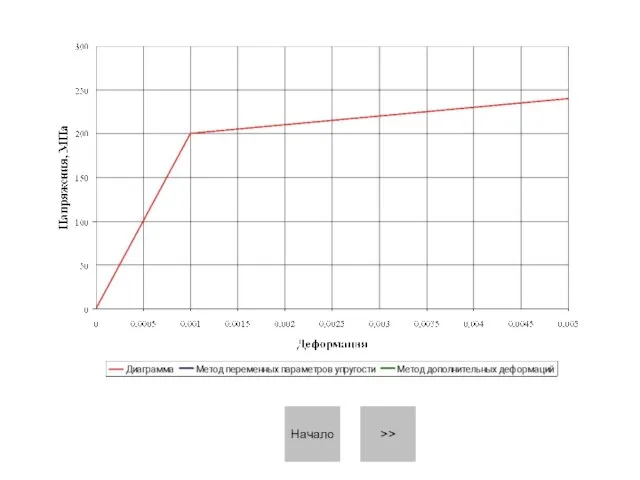
- 15. >> Начало
- 17. Скачать презентацию


 ООО «ЭкоЛайф 69»
ООО «ЭкоЛайф 69» Борьба Руси с иноземным нашествием в XIII в.
Борьба Руси с иноземным нашествием в XIII в. Формы и методы развития исследовательских способностей
Формы и методы развития исследовательских способностей Подбор, обучение и мониторинг персонала Call центров.
Подбор, обучение и мониторинг персонала Call центров. Наследственное право РФ
Наследственное право РФ Приготовление пресного сдобного теста и изделий из него
Приготовление пресного сдобного теста и изделий из него Парковая зона театра им. Натальи Сац
Парковая зона театра им. Натальи Сац правда и вымыслы об акулах
правда и вымыслы об акулах 1. ПР №1 - Тема -1ч. Развитие психики и сознания
1. ПР №1 - Тема -1ч. Развитие психики и сознания Презентация на тему Личные финансы
Презентация на тему Личные финансы Маленькая фея: новинки
Маленькая фея: новинки Настенная живопись
Настенная живопись Комплексное обеспечение процессов в сфере складской логистики, производства и ритейла
Комплексное обеспечение процессов в сфере складской логистики, производства и ритейла Санаторий Марциальные воды в Карелии. Лечение, отдых, встречи
Санаторий Марциальные воды в Карелии. Лечение, отдых, встречи Алгоритм психологической организации группы. Лекция 1
Алгоритм психологической организации группы. Лекция 1 МЕНЕДЖМЕНТ
МЕНЕДЖМЕНТ Современные принципы государственной политики в области МСБ: налоговое регулирование, доступ к финансам
Современные принципы государственной политики в области МСБ: налоговое регулирование, доступ к финансам О финансировании медицинских организаций в системе ОМС в 2011 году и перспективах перехода на одноканальное финансирование в 2011-201
О финансировании медицинских организаций в системе ОМС в 2011 году и перспективах перехода на одноканальное финансирование в 2011-201 Выборы президента школы
Выборы президента школы Оценка информированности учащихся ГБОУ СОШ № 499 по проблемам, связанным с потреблением наркотиков
Оценка информированности учащихся ГБОУ СОШ № 499 по проблемам, связанным с потреблением наркотиков Н.Д. Голев
Н.Д. Голев Продажа маральников и земельных участков
Продажа маральников и земельных участков Автономный контроллер освещения
Автономный контроллер освещения Система управления предприятием Облик-ERP.Конфигурация Оперативное управление предприятием.
Система управления предприятием Облик-ERP.Конфигурация Оперативное управление предприятием. Эмоции эмпатии и вины
Эмоции эмпатии и вины Особенности формирования производственного плана в лесной отрасли
Особенности формирования производственного плана в лесной отрасли Презентация на тему Биологическое действие радиоактивных излучений
Презентация на тему Биологическое действие радиоактивных излучений Школа молодого политика Лидер
Школа молодого политика Лидер