Сфера, описанная вокруг многогранника

Определение: Многогранник называется вписанным в сферу (вписанным в шар), если все вершины многогранника принадлежат этой сфере.
Про сферу в этом случае говорят, что сфера описана около многогранника.

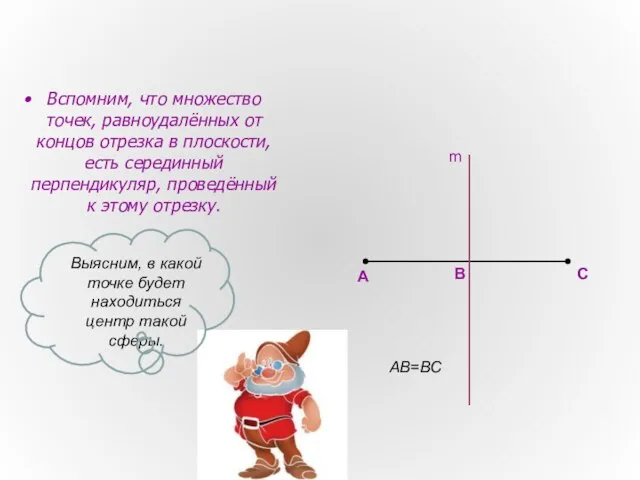
Вспомним, что множество точек, равноудалённых от концов отрезка в плоскости, есть серединный перпендикуляр, проведённый к этому отрезку.
А
В
С
АВ=ВС
m
Выясним, в какой точке будет находиться центр такой сферы.

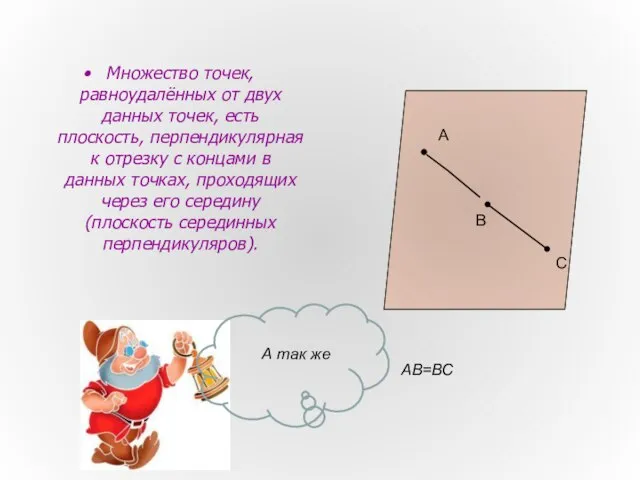
Множество точек, равноудалённых от двух данных точек, есть плоскость, перпендикулярная к отрезку с концами в данных точках, проходящих через его середину (плоскость серединных перпендикуляров).
А
В
С
АВ=ВС
А так же

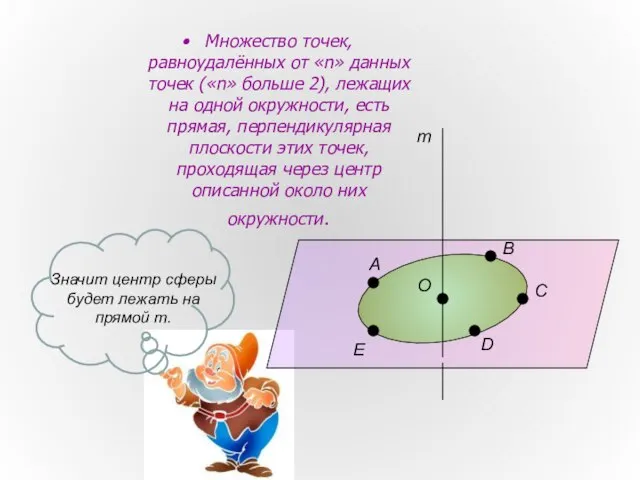
Множество точек, равноудалённых от «n» данных точек («n» больше 2), лежащих на одной окружности, есть прямая, перпендикулярная плоскости этих точек, проходящая через центр описанной около них окружности.
А
В
С
D
E
O
m
Значит центр сферы будет лежать на прямой m.

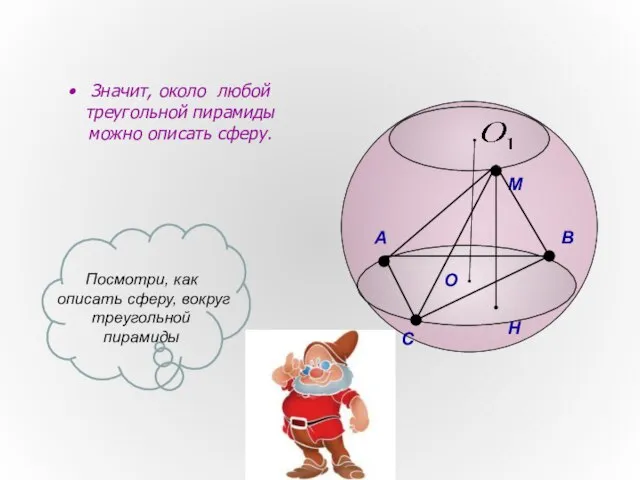
Значит, около любой треугольной пирамиды можно описать сферу.
А
В
С
M
H
O
Посмотри, как описать сферу, вокруг треугольной пирамиды

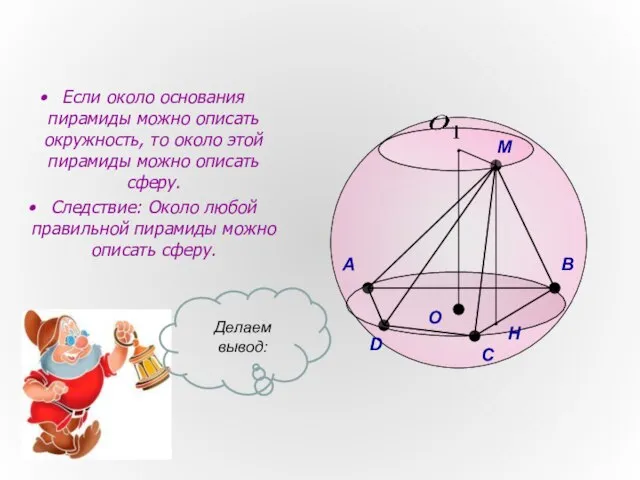
Если около основания пирамиды можно описать окружность, то около этой пирамиды можно описать сферу.
Следствие: Около любой правильной пирамиды можно описать сферу.
А
В
С
D
M
O
H
Делаем вывод:

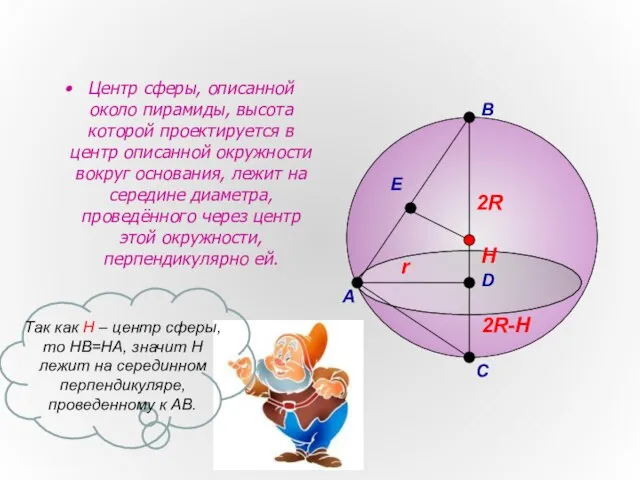
Центр сферы, описанной около пирамиды, высота которой проектируется в центр описанной окружности вокруг основания, лежит на середине диаметра, проведённого через центр этой окружности, перпендикулярно ей.
А
В
С
D
Е
2R
H
r
2R-H
Так как Н – центр сферы, то НВ=НА, значит Н лежит на серединном перпендикуляре, проведенному к АВ.

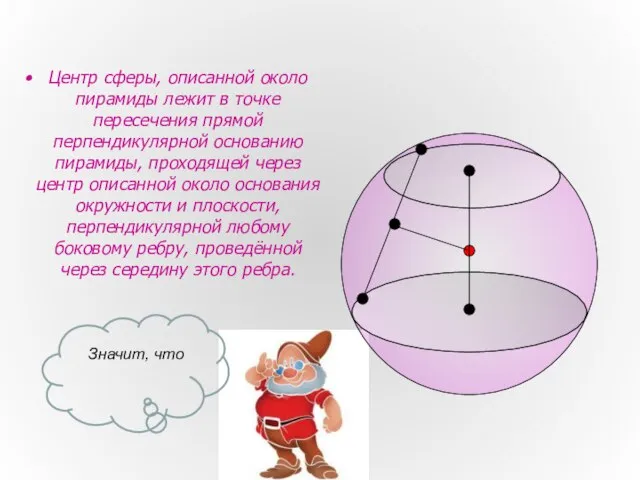
Центр сферы, описанной около пирамиды лежит в точке пересечения прямой перпендикулярной основанию пирамиды, проходящей через центр описанной около основания окружности и плоскости, перпендикулярной любому боковому ребру, проведённой через середину этого ребра.
Значит, что