Содержание
- 2. Определение: Функция F(х) называется первообразной функции f(х) на промежутке Х, если Теорема: Если функция f(х) непрерывна
- 3. Пример: Решение. Данная функция может быть записана в виде:
- 4. Замечание 2: Если функция f(х) определена на промежутке Х и в точке имеет разрыв в виде
- 5. Основные свойства неопределенного интеграла.
- 6. Основные методы Интегрирования.
- 7. Табличный. Сведение к табличному преобразованием подынтегрального выражения в сумму или разность. Интегрирование с помощью замены переменной
- 8. Нахождение интеграла методом преобразования подынтегральной функции в сумму или разность.
- 9. Интегрирование методом замены переменной.
- 11. Интегрирование выражений, содержащих радикалы, методом подстановки.
- 13. Интегрирование алгебраических дробей.
- 14. Интегрирование по частям.
- 17. Скачать презентацию








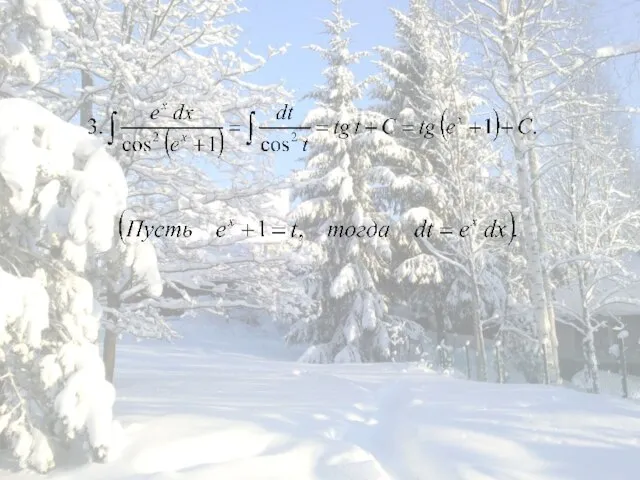





 Ислам. Тест
Ислам. Тест Концепция структурных преобразований радиоэлектронной промышленности оборонно-промышленного комплекса
Концепция структурных преобразований радиоэлектронной промышленности оборонно-промышленного комплекса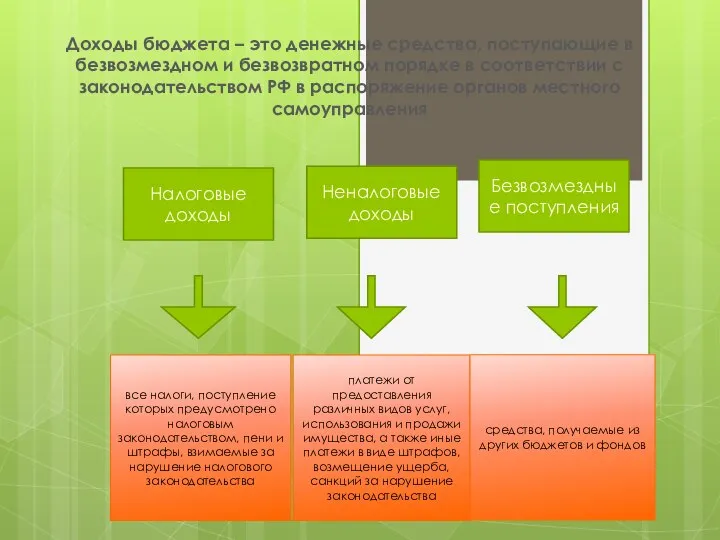 Доходы бюджета Чугунаевского сельского поселения
Доходы бюджета Чугунаевского сельского поселения Деды Морозы в разных странах
Деды Морозы в разных странах Презентация на тему Дорожное движение, безопасность участников дорожного движения (5 класс)
Презентация на тему Дорожное движение, безопасность участников дорожного движения (5 класс) Конкурсная программа «Мы должны быть бережливыми!»
Конкурсная программа «Мы должны быть бережливыми!» Галерея помещиков Мёртвые души
Галерея помещиков Мёртвые души Искусство второй половины XX века.Ташизм, абстрактный экспрессионизм
Искусство второй половины XX века.Ташизм, абстрактный экспрессионизм Производство ферментных препаратов
Производство ферментных препаратов  Общая физическая подготовка
Общая физическая подготовка Придаточные предложения места
Придаточные предложения места Main changes Tudors
Main changes Tudors Сертификация (ап)
Сертификация (ап) Презентация к уроку русского языка в 6 классе по теме Прилагательное как часть речи Составитель: Падалко Татьяна Викторовна
Презентация к уроку русского языка в 6 классе по теме Прилагательное как часть речи Составитель: Падалко Татьяна Викторовна  Презентация на тему Характер
Презентация на тему Характер Организация и нормативно-правовое обеспечение государственной (итоговой) аттестации выпускников 9-х классов в 2009-2010 учебном
Организация и нормативно-правовое обеспечение государственной (итоговой) аттестации выпускников 9-х классов в 2009-2010 учебном  Александр Сергеевич Пушкин
Александр Сергеевич Пушкин Ответственность директоров и контролирующего лица
Ответственность директоров и контролирующего лица Организация внеурочной деятельности при реализации федерального государственного образовательного стандарта начального общего
Организация внеурочной деятельности при реализации федерального государственного образовательного стандарта начального общего Презентация на тему Загадки с подвохом
Презентация на тему Загадки с подвохом Век XVIII в истории России
Век XVIII в истории России Законы и нормативно-правовые акты по организации безопасности по условиям РСЧС
Законы и нормативно-правовые акты по организации безопасности по условиям РСЧС БОРТОВАЯ АНАЛИТИЧЕСКАЯ СИСТЕМА УПРАВЛЕНИЯ РИСКАМИ ПОЛЕТА САМОЛЕТА
БОРТОВАЯ АНАЛИТИЧЕСКАЯ СИСТЕМА УПРАВЛЕНИЯ РИСКАМИ ПОЛЕТА САМОЛЕТА ИМИДЖ КАК ФАКТОР КОНКУРЕНТОСПОСОБНОСТИ ВЫСШЕГО УЧЕБНОГО ЗАВЕДЕНИЯ
ИМИДЖ КАК ФАКТОР КОНКУРЕНТОСПОСОБНОСТИ ВЫСШЕГО УЧЕБНОГО ЗАВЕДЕНИЯ Формы ДНК
Формы ДНК Инфекционный перитонит кошек
Инфекционный перитонит кошек Правила выплат нуждающимся в поддержке семьям на детей от 3 до 7 лет
Правила выплат нуждающимся в поддержке семьям на детей от 3 до 7 лет S-Иерархия и атрибуты маршрутов
S-Иерархия и атрибуты маршрутов