Сфера и шар

СФЕРА
И
ШАР

Поверхность шара называют сферой или шаровой поверхностью.
Сфера - по-гречески так назывался мяч, в который играли дети.

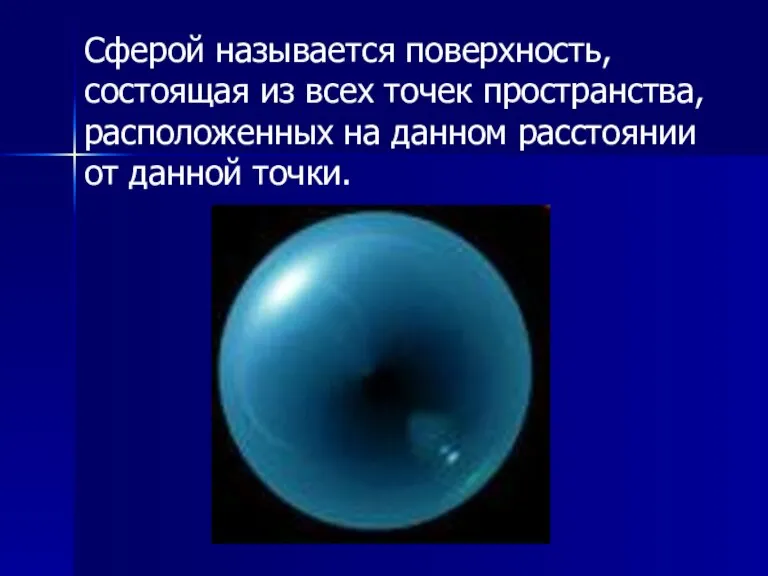
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.

Элементы сферы
R
O
Отрезок, соединяющий центр и какую-нибудь точку сферы называется
радиусом (R).
Отрезок, соединяющий две точки сферы
и проходящий через её центр называется диаметром (D).
M
D=2R

Возможны три случая решения:
1) d
2) d=R
3) d>R

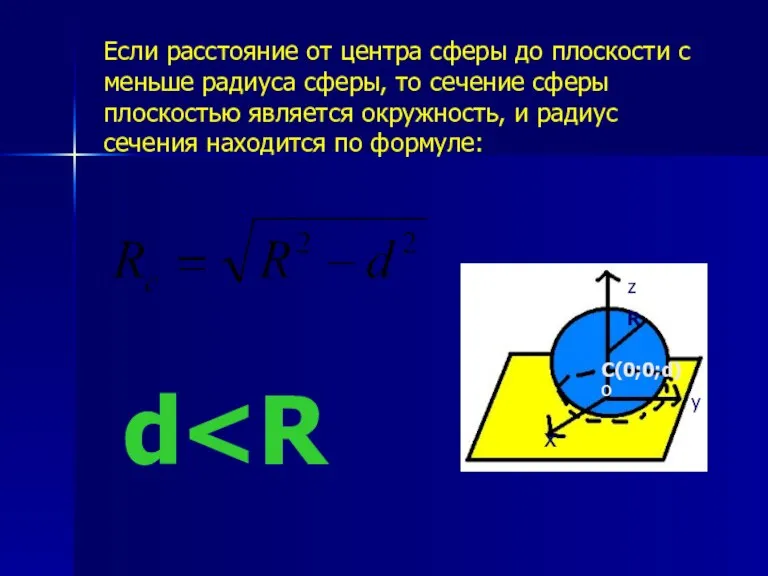
Если расстояние от центра сферы до плоскости с меньше радиуса сферы, то сечение сферы плоскостью является окружность, и радиус сечения находится по формуле:
R
C(0;0;d)
о
х
у
z
d

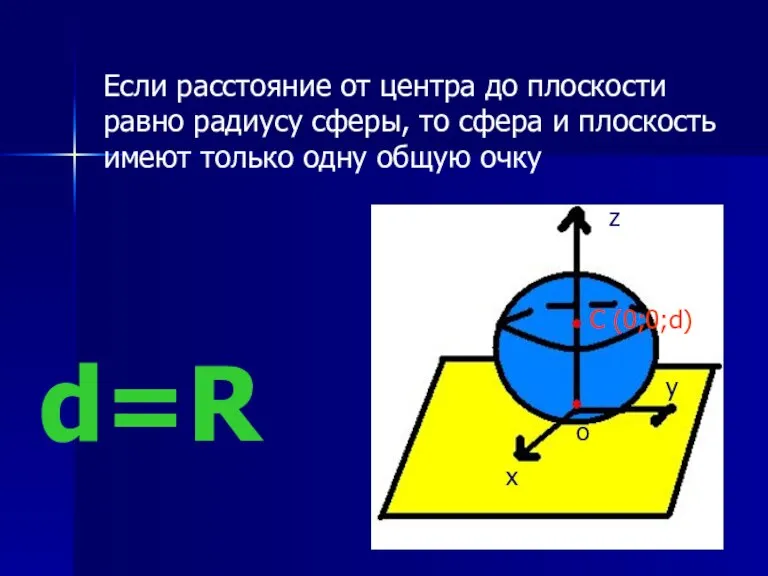
Если расстояние от центра до плоскости равно радиусу сферы, то сфера и плоскость имеют только одну общую очку
d=R
z
у
х
о
С (0;0;d)

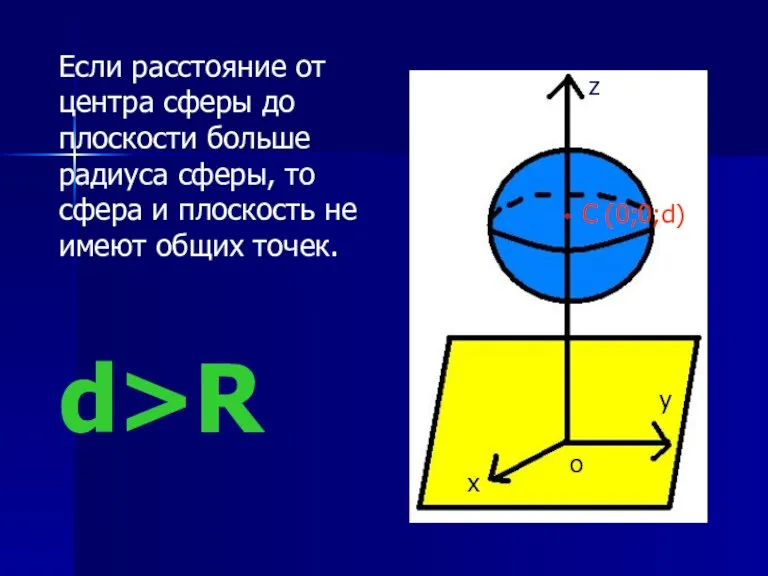
Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.
о
х
у
z
С (0;0;d)
d>R

Шар – это тело, образованное вращением полукруга вокруг оси, содержащей его диаметр.
А
С
В

СЕЧЕНИЯ
ШАРА И СФЕРЫ

Если рассечь сферу плоскостью, в сечении получится окружность.
Такие окружности имеют разные радиусы: чем дальше от центра, тем меньше радиус сечения. Самые большие окружности получаются при сечении сферы плоскостями, проходящими через центр. Такими большими окружностями на земной поверхности являются экватор и меридианы. А параллели – это сечения земной поверхности плоскостями, параллельными плоскости экватора.

Сечением шара является круг.
Сечение шара плоскостью, проходящей через его центр, называют большим кругом шара.