Содержание
- 2. научить распознавать симметричные фигуры среди других; познакомить учащихся с использованием симметрии в природе, быту, искусстве, технике;
- 3. Симметричность точек относительно прямой Симметричность фигуры относительно прямой Симметричность точек относительно точки Симметричность фигуры относительно точки
- 4. “Симметрия (от греческого symmetria - «соразмерность») - понятие, означающее сохраняемость, повторяемость, «инвариантность» каких-либо особенностей структуры изучаемого
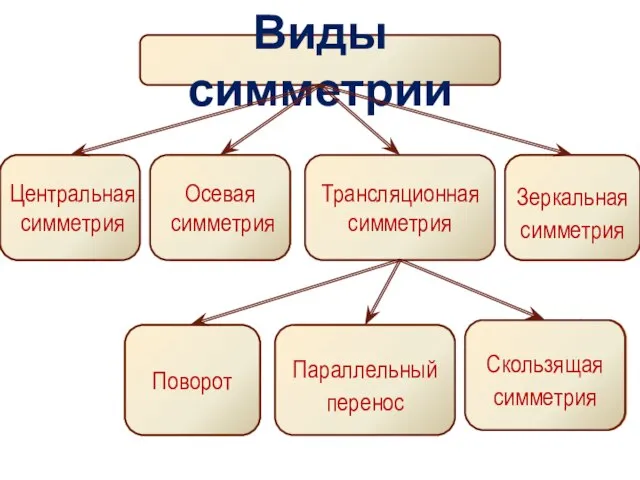
- 5. Виды симметрии Трансляционная симметрия Зеркальная симметрия Поворот Параллельный перенос Скользящая симметрия
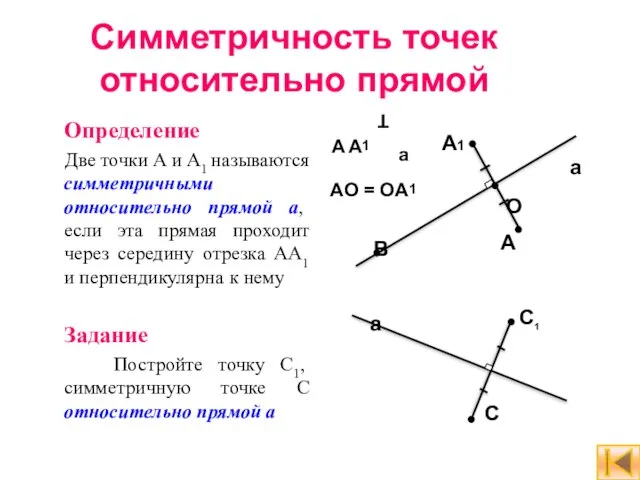
- 6. Симметричность точек относительно прямой Определение Две точки А и А1 называются симметричными относительно прямой а, если
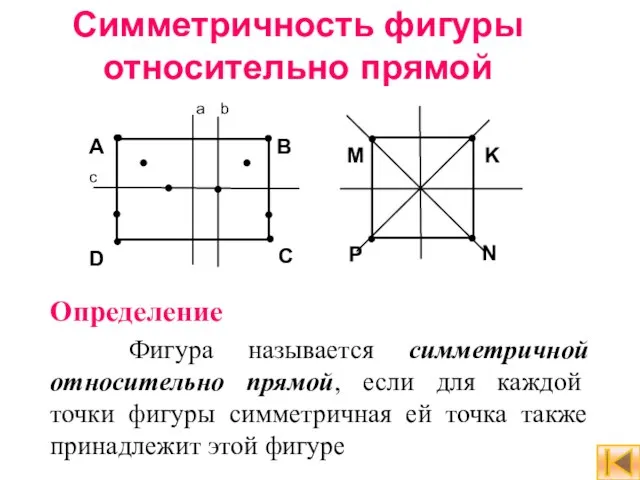
- 7. Симметричность фигуры относительно прямой Определение Фигура называется симметричной относительно прямой, если для каждой точки фигуры симметричная
- 8. Какие из данных фигур имеют ось симметрии? Сколько? Подумай!
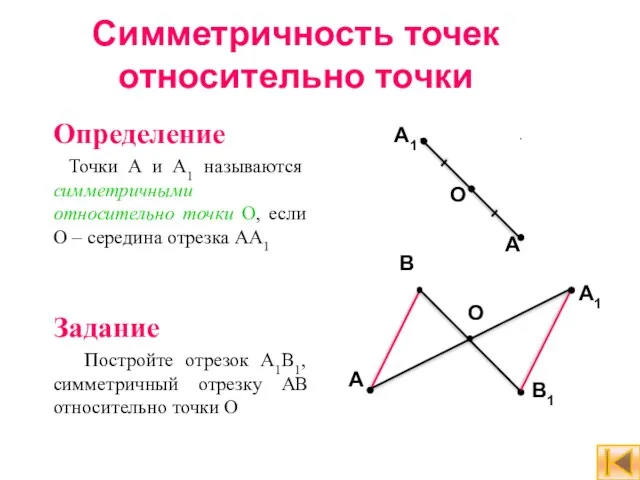
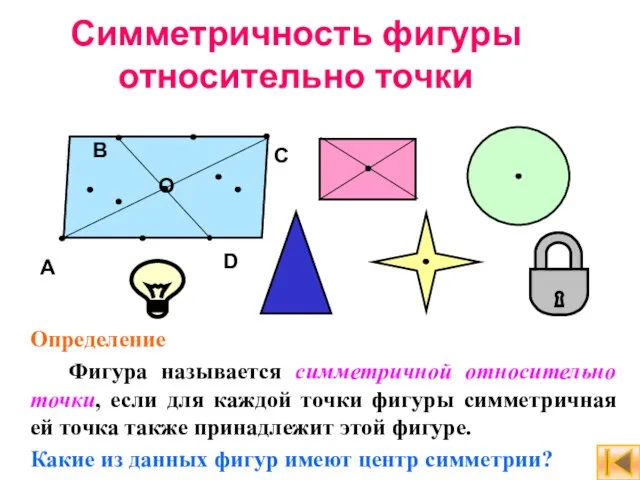
- 9. Симметричность точек относительно точки Определение Точки A и A1 называются симметричными относительно точки О, если О
- 10. Симметричность фигуры относительно точки Определение Фигура называется симметричной относительно точки, если для каждой точки фигуры симметричная
- 11. Осевая симметрия
- 12. Центральная симметрия
- 13. Нетрадиционные виды симметрии Винтовая симметрия Симметрия поворота Переносная симметрия
- 14. Винтовая симметрия
- 15. Переносная симметрия или скользящее преобразование
- 16. Симметрия поворота
- 17. Симметрия в природе
- 18. Симметрия в архитектуре
- 19. Часто такую симметрию называют зеркальной. А зеркало не просто копирует объект, но и меняет местами передние
- 20. Предметы
- 21. Симметрия танца
- 22. Симметрия в литературе Палиндром - это абсолютное проявление симметрии в литературе. Например: «А луна канула», «А
- 23. «Симметричные» профессии И Н Ж Е Н Е Р Г Е Н Е Т И К
- 24. Математики о симметрии Математик любит прежде всего симметрию Максвелл Д. Красота тесно связана с симметрией Вейль
- 25. Заключение Симметрия играет огромную роль в искусстве: в архитектуре, в музыке, в поэзии; природе: у растений
- 27. Скачать презентацию


















 Разложение многочленов на множители
Разложение многочленов на множители Презентация на тему Внутреннее строение Cолнца
Презентация на тему Внутреннее строение Cолнца  Раздел 1. Общая психология_Лекция 1_Психология как наука
Раздел 1. Общая психология_Лекция 1_Психология как наука Эволюция приматов 9 класс
Эволюция приматов 9 класс Тыва тоннарның хевирлери болгаш шын адаары
Тыва тоннарның хевирлери болгаш шын адаары Подготовка к ГИА с использованием ИКТ
Подготовка к ГИА с использованием ИКТ Презентация на тему Музыкальная драматургия - развитие музыки (7 класс)
Презентация на тему Музыкальная драматургия - развитие музыки (7 класс) Тема 7. Линейная модельпроизводственной структуры сельскохозяйственной организациина долгосрочную перспективу
Тема 7. Линейная модельпроизводственной структуры сельскохозяйственной организациина долгосрочную перспективу Клетка
Клетка Л.Н.Толстой Рассказ «После бала»
Л.Н.Толстой Рассказ «После бала» Проект
Проект Kursovaya_rabota
Kursovaya_rabota ГБУ ДО ДДЮ Приморского района
ГБУ ДО ДДЮ Приморского района Electronic Reserve System (eReserve)
Electronic Reserve System (eReserve) Доказательства происхождения классов позвоночных животных
Доказательства происхождения классов позвоночных животных Болезнь и синдром Рейно
Болезнь и синдром Рейно Модульные строительные конструкции на основе сталефибробетонной несъемной опалубки
Модульные строительные конструкции на основе сталефибробетонной несъемной опалубки Аппликация из крашеных опилок
Аппликация из крашеных опилок Технологическое предпринимательство для школьников: от изобретения к бизнесу! Занятие 1
Технологическое предпринимательство для школьников: от изобретения к бизнесу! Занятие 1 Ҡол Ғәли Йософ ҡиссаһы
Ҡол Ғәли Йософ ҡиссаһы Автоматизированная система пуска синхронных и асинхронных двигателей низкого и высокого напряжений
Автоматизированная система пуска синхронных и асинхронных двигателей низкого и высокого напряжений Декоративно-пркладное искусство России
Декоративно-пркладное искусство России Каркас унифицированный безригельный КУБ 2,5
Каркас унифицированный безригельный КУБ 2,5 Краткое описание. Бизнес проект по открытию ресторана фаст-фуд с последующим развитием сети. Рестораны фаст-фуд – предприятия общ
Краткое описание. Бизнес проект по открытию ресторана фаст-фуд с последующим развитием сети. Рестораны фаст-фуд – предприятия общ Презентация на тему Организация проектной деятельности учащихся на уроках биологии
Презентация на тему Организация проектной деятельности учащихся на уроках биологии  Государственный контроль за качеством образования
Государственный контроль за качеством образования Гражданин РФ
Гражданин РФ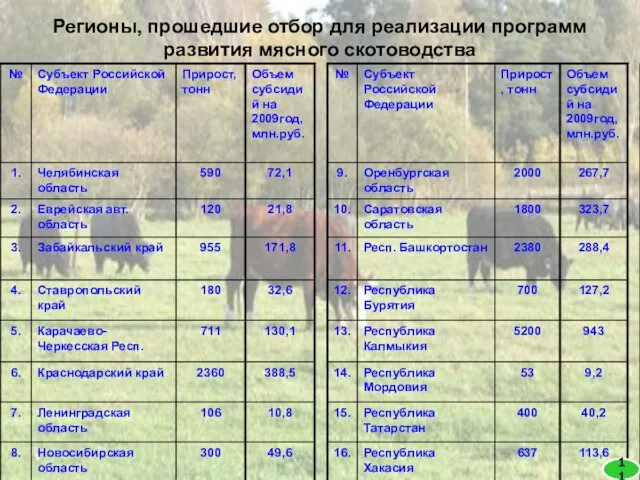 Регионы, прошедшие отбор для реализации программ развития мясного скотоводства
Регионы, прошедшие отбор для реализации программ развития мясного скотоводства