Содержание
- 2. Система счисления 1.Это способ изображения чисел и соответствующие ему правила действия над числами. 2.Это способ записи
- 3. Все системы счисления Позиционные Непозиционные
- 4. Непозиционная С.С. В таких с.с. от положения знака в записи числа не зависит величина, которую он
- 5. Непозиционная С.С. I=1 V=5 X=10 L=50 C=100 D=500 M=1000
- 6. Непозиционная С.С. CCXXXII Складывается из двух сотен, трех десятков и двух единиц и равно 232.
- 7. Непозиционная С.С. Правила записи: Цифры записываются слева направо в порядке убывания и их значения складываются. Если
- 8. Непозиционная С.С. Были более или менее пригодны для выполнения сложения и вычитания, но непригодны для выполнения
- 9. Позиционная С.С. Величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Основание позиционной С.С. –
- 10. Позиционная С.С. 2749 2 *103 + 7*102 + 4*101+9*100 2000+700+40+9=2749 384,9506 3*102 +8*10 + 4+ 9*10-1+5*10-2+6*10-4=
- 11. Преимущества десятичной системы счисления не математические, а зоологические. Если бы у нас на руках было не
- 12. Позиционная С.С. Для записи чисел в позиционной системе с основанием n нужно иметь алфавит из n
- 13. Позиционная С.С. Вот примеры алфавитов нескольких систем:
- 14. Основание системы, к которой относится число обозначается подстрочным индексом: 1011012, 36718, 3В8Е16 Позиционная С.С.
- 15. Перевод чисел из одной с.с. в другую 1123=1 *32+1*31+2*30=9+3+2=14 1011012=1*25+0*24+1*23+1*22+0*21+1*20 Обратный перевод: 1510=8+4+2+1=1*22+1*22+1*21+1=11112
- 16. Перевод чисел из одной с.с. в другую Как перевести 15710= ?2
- 17. Сложение в двоичной с.с. В основе сложения чисел в двоичной системе счисления лежит таблица сложения одноразрядных
- 18. Сложение в двоичной с.с. Важно обратить внимание на то, что при сложении двух единиц производится перенос
- 19. Проверим правильность вычислений 1102=1*22+1*21+0*20=610 112=1*21+1*20=310 10012=1*23+0*22+0*21+1*20=910 610+310=910 Сложение выполнено верно.
- 20. Вычитание в двоичной с.с. В основе вычитания двоичных чисел лежит таблица вычитания одноразрядных двоичных чисел. При
- 21. Вычитание в двоичной с.с. Для примера производим вычитание двоичных чисел 1102 и 112: 112
- 22. Умножение чисел в двоичной с.с. В основе умножения лежит таблица умножения одноразрядных двоичных чисел.
- 23. Умножение чисел в двоичной с.с. Рассмотрим пример умножения двоичных чисел 1102 и 112: 110 110 100102
- 24. Деление чисел в двоичной с.с. Выполняется подобно операции деления в десятичной с.с. Разделим двоичное число 1102
- 25. Задания Чему равны в десятичной с.с. следующие числа:XI, IX, LX, CLX, MDCXLVIII. Запишите римскими цифрами числа:
- 26. Задания 3. Переведите числа из одной системы счисления в другую: 5610=?2 11112=?10 23С16=?10 5610=?8 5610=?5 1788=?10
- 28. Скачать презентацию
























 Теоретико-методологические ориентиры инклюзивного образования
Теоретико-методологические ориентиры инклюзивного образования Судьба свободолюбивой личности в романтической поэме М.Ю.Лермонтова «Мцыри»
Судьба свободолюбивой личности в романтической поэме М.Ю.Лермонтова «Мцыри» Tauride Gardens or Tavrichesky Garden
Tauride Gardens or Tavrichesky Garden  Почему Лига Наций не смогла сохранить мир после Первой мировой войны
Почему Лига Наций не смогла сохранить мир после Первой мировой войны Рисуем рыбку
Рисуем рыбку Интеллектуальная электроэнергетика
Интеллектуальная электроэнергетика 222 группа. Лукояновский педагогический колледж им. А.М. Горького
222 группа. Лукояновский педагогический колледж им. А.М. Горького Задачи апробации электронных учебников
Задачи апробации электронных учебников Законодательные возможности участия граждан в управлении природными ресурсами
Законодательные возможности участия граждан в управлении природными ресурсами Шоколад
Шоколад Приемная кампания 2021 в АПОУ УР ГАПТ
Приемная кампания 2021 в АПОУ УР ГАПТ Презентация на тему Цепи питания
Презентация на тему Цепи питания  Неотложная терапия для детей
Неотложная терапия для детей Презентация на тему Средневековый город и его обитатели
Презентация на тему Средневековый город и его обитатели  Презентация на тему Пейзаж и его разновидности
Презентация на тему Пейзаж и его разновидности Круговой метод тренировки
Круговой метод тренировки Об амфибиях и рептилиях, которых многие совсем не любят
Об амфибиях и рептилиях, которых многие совсем не любят Презентация на тему Не с существительными (5 класс)
Презентация на тему Не с существительными (5 класс) Презентация на тему Строчная буква с
Презентация на тему Строчная буква с  Коммуникация как инструмент управления командой
Коммуникация как инструмент управления командой Презентация на тему Эпоха Петра 1
Презентация на тему Эпоха Петра 1 Времена года в творчестве А.С. Пушкина
Времена года в творчестве А.С. Пушкина Неопределённые местоимения
Неопределённые местоимения Модульный курс для аспирантов «Некоторые дискуссионные проблемы в современном страховании» Гомелля Владимир Борисович к.э.н.,
Модульный курс для аспирантов «Некоторые дискуссионные проблемы в современном страховании» Гомелля Владимир Борисович к.э.н.,  Приемы наблюдения за противником и местностью, действиями соседей и за сигналами командира на месте и в движении
Приемы наблюдения за противником и местностью, действиями соседей и за сигналами командира на месте и в движении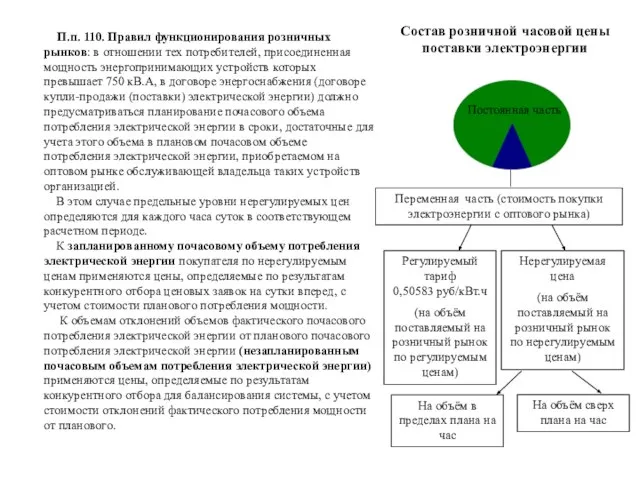 Состав розничной часовой цены поставки электроэнергии
Состав розничной часовой цены поставки электроэнергии Солнечный Сидней
Солнечный Сидней Компьютерная зависимость
Компьютерная зависимость