Содержание
- 2. Уравнение записывают одно под другим и объединяют фигурной скобкой. Порядок уравнений не играет роли. Например: х+у=39
- 3. Система двух уравнений, из которых одно первой степени, а другое второй. Система уравнений вида: х +
- 4. Пусть дана система: 4 у + х + 3у = 1 2 х – = Воспользуемся
- 5. Тогда уравнение 2-й степени после подстановки дает уравнение с одним неизвестным х: 4 у + х
- 6. Решаем уравнение - 4(2х-1) + х + 3(2х-1)=1 2 х – 4 (2х-1) + х +
- 7. 15 х - 23 х + 8 = 0 2 √D = √23 – 4 ×
- 8. После этого из уравнения у = 2х — 1 находим: у1 = 2 - 1 у2=
- 9. Ответ: ( 1; 1) ;(8/15 ; 1/15) Таким образом, данная система имеет две пары решений: 1)
- 10. Система двух уравнений, из которых каждое второй степени. Пример: x + y = а х у
- 11. Если b = 0, то и х = 0 и у = 0 . Поэтому мы
- 12. Умножив обе части на x , получим равносильное уравнение: x + b = ax , т.
- 13. Подобным же образом решается и система: x² — y² = а xy = b. Подобным же
- 14. Надо решить систему уравнений:
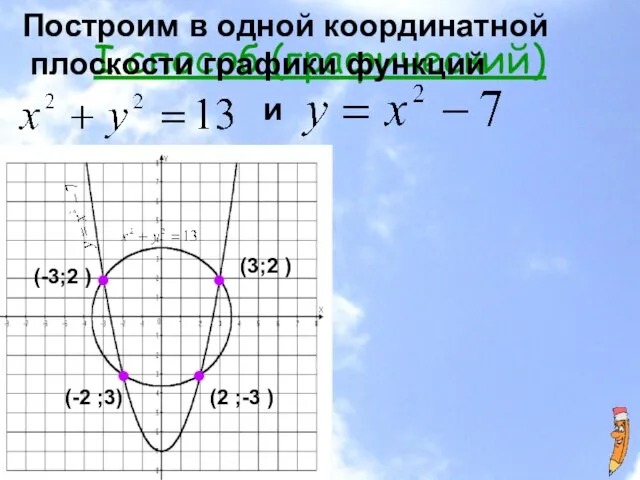
- 15. I способ (графический) Построим в одной координатной плоскости графики функций х ² + у ² =
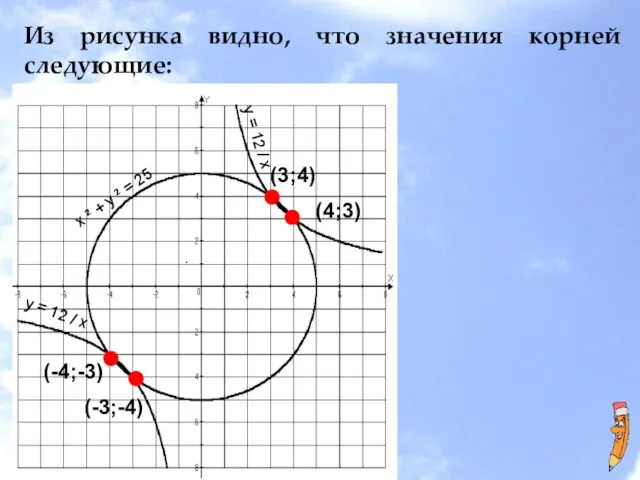
- 16. Из рисунка видно, что значения корней следующие: . х ² + у ² = 25 у
- 17. II способ (аналитический) Умножим второе уравнение на 2 и сначала сложим с первым, а затем вычтем
- 18. Задача сводится к системе линейных уравнений с двумя неизвестными:
- 19. Применяя к полученным системам метод сложения (т.е. сперва сложим эти уравнения, а далее вычтем из первых
- 20. Решить систему уравнений:
- 21. I способ (графический) Построим в одной координатной плоскости графики функций и (-3;2 ) (-2 ;3) (3;2
- 23. Скачать презентацию





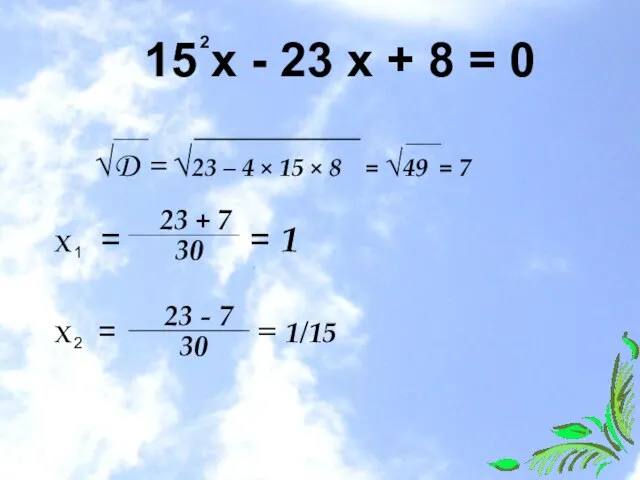












 Экспресс-викторина по «Денискиным рассказам» В.Ю.Драгунского
Экспресс-викторина по «Денискиным рассказам» В.Ю.Драгунского Презентация Microsoft PowerPoint (3)
Презентация Microsoft PowerPoint (3) Закуски из мяса.11 класс
Закуски из мяса.11 класс Критерии оценивания урока в системно-деятельностном подходе
Критерии оценивания урока в системно-деятельностном подходе z1516981307
z1516981307 Самое великое великое чудо на свете
Самое великое великое чудо на свете Структура ВС, функции
Структура ВС, функции 12.09-16.09
12.09-16.09 Проблемы подростковой среды
Проблемы подростковой среды Атмосфера. Вес воздуха
Атмосфера. Вес воздуха Why are people fond of sport
Why are people fond of sport Новое поколение IP домофонов компании Метаком
Новое поколение IP домофонов компании Метаком Соединенные штаты Америки во второй половине XIX века
Соединенные штаты Америки во второй половине XIX века 3 жас дағдарысы баланың мен. Концепциясының қалыптасу кезеңі
3 жас дағдарысы баланың мен. Концепциясының қалыптасу кезеңі Основная специализация детского психолога – коррекция взаимоотношений ребенка с окружающим его миром
Основная специализация детского психолога – коррекция взаимоотношений ребенка с окружающим его миром А У Д И Т О Р С К И Е У С Л У Г И
А У Д И Т О Р С К И Е У С Л У Г И Жалюзи
Жалюзи Жидкие кристаллы
Жидкие кристаллы ИТС и дорожная безопасность
ИТС и дорожная безопасность ПЛАН ПОДГОТОВКИ К ЕГЭ 2012
ПЛАН ПОДГОТОВКИ К ЕГЭ 2012 Системи лінійних алгебраичних рівнянь (СЛАР) основні відомості
Системи лінійних алгебраичних рівнянь (СЛАР) основні відомості Проект Территория Т
Проект Территория Т Титульный лист
Титульный лист Основные туристические центры России
Основные туристические центры России Great Britain
Great Britain  Психологические основы педагогического общения
Психологические основы педагогического общения History of language
History of language Конкурс матрёшки
Конкурс матрёшки