Сложение и умножение числовых неравенств.

Устная работа:
а) Сформулируйте теоремы, выражающие основные свойства числовых неравенств.
в) Дано: а>в.
Сравните:
4а и 4в;
—23а и —23в.
г) Дано: 2<х<4. Оцените значение выражения:
2х; —3х;

Теорема 5.
Если а
Доказательство.
Прибавив к обеим частям неравенства a < b число с, получим а + с < b + с.
Прибавив к обеим частям неравенства с
Из неравенств а + с < b + с и
b + с < b + d следует, что
а +с < b + d.

Вывод:
Если сложить почленно верные неравенства одного знака, то получится верное неравенство.

Например:
—5<12 2. —6>—10
+ 8<20 + 11>—6 3<32 верное 5 > —16 верное неравенство неравенство

Теорема 6.
Если а < b и с < d, где а, b, с, d— положительные числа, то ас < bd.
Доказательство:
Умножив обе части неравенства а < b на положительное число с, получим ас < bс.
Умножив обе части неравенства с < d‚на положительное число b, получим bс
Из неравенств ас < bс и bс < bd следует, что
ас < bd.

ВЫВОД:
Если перемножить почленно верные неравенства одного знака, левые и правые части которых — положительные числа, то получится верное неравенство.

Например:
1) х 8>3 2) 0,9 >0,1 10>2 х 1 > 1
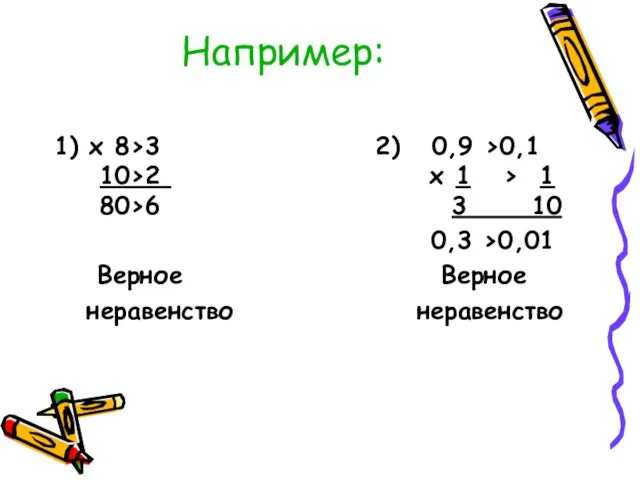
80>6 3 10
0,3 >0,01
Верное Верное
неравенство неравенство

Заметим:
если в неравенствах а < b и с < d среди чисел а, b, с, d имеются отрицательные, то неравенство ас < bd может оказаться неверным.
например:
перемножив почленно верные неравенства
— З < —2 и —5 < 6, получим неравенство 15 <—12 которое не является верным.

Закрепление:
№ 747
№ 748

Работа над пройденным материалом:
№ 849 (б; г)
№ 746.

Итог урока:
Какие выводы мы сделали на уроке?