Слайд 2Общее понятие о средних величинах

Слайд 3 Средняя величина – это обобщающая количественная характеристика совокупности по изучаемому признаку в

конкретных условиях места и времени. Средняя величина отражает то общее и типичное, что присуще единицам данной совокупности
Слайд 4 В средних величинах погашаются индивидуальные отклонения, соответствующие отдельным единицам совокупности. Чтобы средняя

величина имела смысл, она должна рассчитываться для однородной совокупности
Слайд 5 Используя среднюю, мы можем одним числом охарактеризовать изучаемое явление. По уточненным данным

Всероссийской переписи населения 2002 года, средний размер семьи составляет 2,7 чел. В городских населенных пунктах – 2,7. В сельских – 2,8. Подробную информацию найдете на http://www.perepis2002.ru/ct/doc/TOM_06_01.xls
Слайд 6 Самое малое значение этого показателя 2,2 в сельской местности Псковской области, самый

большой – 7,4 выявлен в сельской местности Республики Ингушетия
Слайд 7 Получив результат 2,7 в среднем по России, мы можем сделать вывод, что

наибольший удельный вес занимают семьи, состоящие из двух, но чаще из трех человек. Безусловно, есть семьи, состоящие из 1 человека (поэтому в статистике говорят не о семье, а о домохозяйстве), из 4, 5, из 6 и более человек. Но вы не найдете ни одной семьи, состоящей из 2,7 человек, потому что число членов домохозяйства – показатель целочисленный
Слайд 8 Необходимые условия для расчета СВ – качественная однородность совокупности: все единицы совокупности

должны обладать изучаемым признаком. Если изучают средний размер стипендии, то каждая единица должна обладать свойством – получением стипендии
Слайд 9 Нельзя, например, подсчитать среднюю стипендию в Бишкеке, потому что не все жители

Бишкека, и даже не все студенты, проживающие в городе, эту самую стипендию получают
Слайд 10 То же можно сказать о пенсии, к примеру, в Москве или зарплате

в Белграде. Поэтому в отношении такой статистической совокупности, как население некоторого населенного пункта, правильнее говорить о среднем доходе на одного жителя
Слайд 11Средняя величина
Среднюю стипендию можно подсчитать среди тех, кто получает стипендию, то же

относится к пенсии и зарплате
Слайд 12Логическая формула
Расчет средней начинается с определения логической формулы. Прежде чем что-то умножать,

делить или складывать, необходимо составить исходное соотношение средней, иначе называемое логической формулой
Слайд 14Исходное соотношение средней
где
А – объем изучаемого события в совокупности: это

суммарная абсолютная величина;
В – объем совокупности: это число единиц совокупности.
ИСС дает нам уровень изучаемого события в расчете на единицу совокупности
Слайд 15Примеры средних
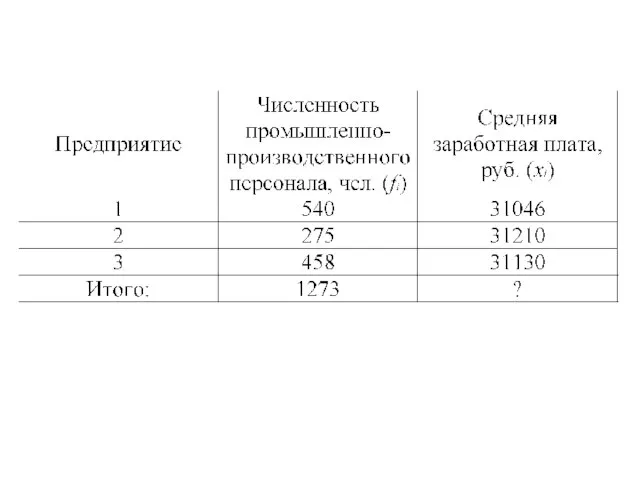
Средняя зарплата показывает, сколько получает один работник. Что же мы возьмем

в числителе и знаменателе ИСС?
А – сумма начисленных средств всем работникам = фонд зарплаты;
В – численность работников
Слайд 16Примеры средних
Зарплата индивидуального работника – это индивидуальная величина. Фонд зарплаты – суммарная

величина, а средняя зарплата – средняя величина
Слайд 17Примеры средних
Средняя цена показывает, сколько в среднем стоит данный товар. Что же

мы возьмем в числителе и знаменателе ИСС?
А – выручка от реализации всего товара = товарооборот;
В – сколько единиц товара продано всего = количество проданного товара
Слайд 18Примеры средних
Средняя себестоимость показывает, сколько в среднем стоит производство единицы продукции. Что

же мы возьмем в числителе и знаменателе ИСС?
А – затраты на производство продукции = в экономической теории это называется издержками производства;
В – выпуск продукции = количество произведенной продукции
Слайд 19Примеры средних
Средний возраст показывает, сколько в среднем лет исследуемой совокупности единиц, не

обязательно одушевленных - это может быть средний возраст автомобилей, студентов, зданий, куриц. Что же мы возьмем в числителе и знаменателе ИСС?
А – суммарное количество лет;
В – количество обследуемых единиц
Слайд 20Примеры средних
Средняя продолжительность жизни, или средний срок службы показывает, сколько в среднем

лет живет одушевленная единица совокупности и служит неодушевленная. Что же мы возьмем в числителе и знаменателе ИСС?
А – суммарное количество лет жизни (службы);
В – количество обследуемых единиц
Слайд 21Логическая формула
Для конкретного экономического показателя может быть составлена ТОЛЬКО ОДНА ИСТИННАЯ

логическая формула
Слайд 22Виды средних величин
Математикой доказано, что большую часть средних, которыми мы пользуемся,

можно выразить в общем виде формулой средней степенной
Слайд 23 Средние величины, применяемые в статистике, относятся к классу степенных средних. Общая

формула степенной средней имеет следующий вид:
_
где x k – степенная средняя k-ого порядка;
k – показатель степени, определяющий форму средней; х – варианты;
n – количество вариант
Слайд 24 Если k =1, получается средняя арифметическая:

Слайд 25 если k =2, получается средняя квадратическая:

Слайд 26 если k =0, получается средняя геометрическая:

Слайд 27 если k = (-1), получается средняя гармоническая:
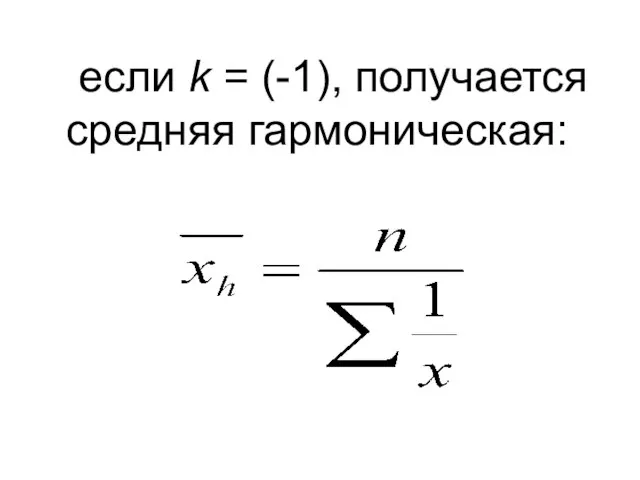
Слайд 28Правило мажорантности
Чем выше показатель степени в формуле степенной средней, тем больше значение

средней
Слайд 30Существуют две формулы средней арифметической:
где f - веса

Слайд 31Средняя арифметическая простая
Средняя арифметическая простая применяется, когда есть перечисление вариант и нет

никаких группировок.
В числителе мы собираем сумму вариант, в знаменателе – количество вариант
Слайд 32Производительность труда 5-и рабочих составляет: 58, 50, 46, 44, 42 изделий за

смену. Определить среднюю производительность труда 5-и рабочих. В этом случае решение имеет следующий вид:
Слайд 33Средняя арифметическая взвешенная
Средняя арифметическая взвешенная используется при появлении группировок. Это самая распространенная

степенная средняя
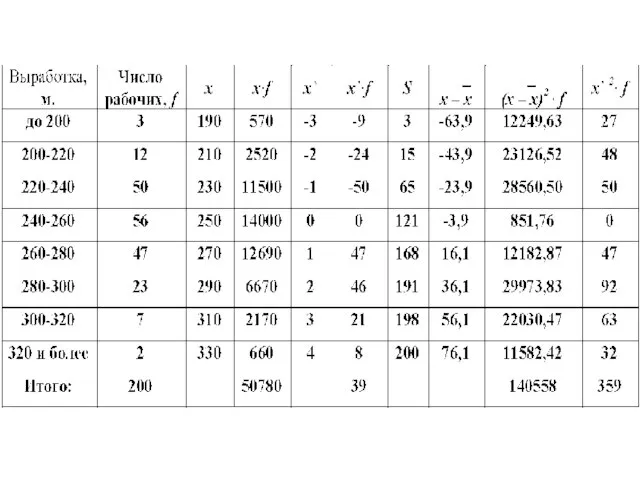
Слайд 35Расчет средней арифметической для вариационного ряда

Слайд 38Модификация формулы
Если f – частость (дается удельный вес в совокупности), то классическая

формула средней арифметической взвешенной не применяется, используют ее модификацию:
Слайд 41Модификация формулы
По существу, мы умножаем варианту на ОВСтруктуры в коэффициентах, в долях

Слайд 431. Произведение средней арифметической и суммы частот равно общему объему изучаемого события

в совокупности (см. формулу ИСС):
Слайд 442. Сумма отклонений всех вариант от средней величины всегда равна 0:

Слайд 45
2. Сумма отклонений всех вариант от средней величины всегда равна 0.
Это значит,

что в средней арифметической
взаимопогашаются
отклонения от средней
Слайд 46
2. В нашем примере со средним размером домохозяйства средняя равна 2,7 чел.

Однако есть конкретные значения количества членов каждой конкретной семьи, варианта х=1,2,3,4,5,6 и более.
(1-2,7)*fi=-
(2-2,7)*fi=-
(3-2,7)*fi=+
(4-2,7)*fi=+
(5-2,7)*fi=+
(6-2,7)*fi=+
Итого:0
Слайд 47Свойства САВ
Свойства 3-5 используются для упрощения расчета, когда нужно подсчитать среднюю из

неудобных чисел
Слайд 483. Если каждую варианту уменьшить на постоянную величину а, расчет средней возможен,

но полученная средняя будет меньше на а:
Слайд 494. Если все варианты уменьшить в одно и то же число раз,

то средняя арифметическая уменьшится в то же число раз:
Слайд 505. Если все веса разделить на какую-либо константу а, то новая средняя

от этого не изменится:
Слайд 515. При расчете средней весовой показатель берется на том же уровне и

в числителе, и в знаменателе
Слайд 52Свойства САВ
Если при расчете САВ были использованы ее свойства, то в результате

получаем не нормальную, а преобразованную САВ. Чтобы перейти к нормальной САВ, необходимо произвести обратные операции в обратном порядке
Слайд 53Упрощенный расчет средней арифметической для вариационного ряда

Слайд 54Основан на свойствах средней величины.
h – величина интервала;
c – одна из вариант

ряда, близкая к середине (лежащая в середине);
А – целое число, на которое без остатка сокращаются все частоты
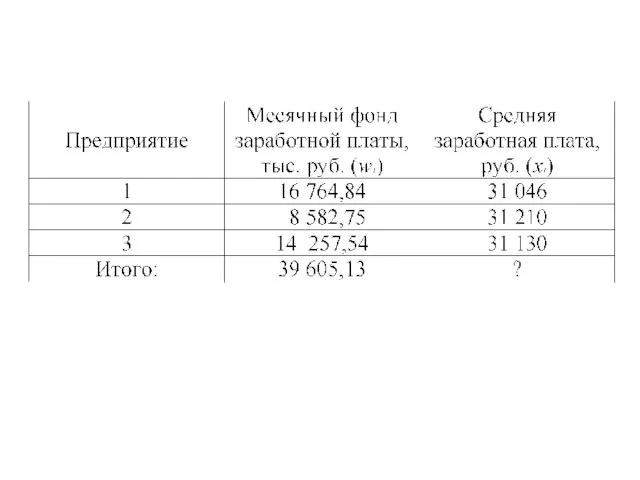
Слайд 58Средняя гармоническая
СГ- это обратная величина средней арифметической. Бывает простая и взвешенная СГ.

Чаще используется взвешенная формула
Слайд 59Существуют две формулы для расчета средней гармонической величины:
где W- сложный вес, объем

события по группе, по конкретному значению
Слайд 61Средняя гармоническая применяется в том случае, когда в качестве весов выступают объемы

изучаемого признака.
Иногда возникает проблема: какую формулу использовать – среднюю гармоническую или среднюю арифметическую? Подходит та формула, у которой и в числителе и знаменателе будут величины, обладающие смыслом
Слайд 62Арифметическая или гармоническая?
Подсказка:
Если по исходной информации дается осредняемая величина (варианта) и знаменатель

логической формулы, то используется САВ.
Если дается варианта и числитель логической формулы, то используется СГВ
Слайд 63Арифметическая или гармоническая?
Иными словами:
Если в ИСС неизвестен числитель, то используется САВ.
Если в

ИСС неизвестен знаменатель, то используется СГВ
Слайд 68Средняя хронологическая
Эта формула средней применяется для ряда моментных показателей

Слайд 69Средняя хронологическая
Необходимо взять половину первого и последнего показателя, плюс моментные показатели, находящиеся

в середине ряда, полученную сумму разделить на (количество моментных показателей минус 1)
Слайд 70Средняя хронологическая
Широко применяется в рядах динамики, в социально-экономической статистике для определения средней

численности населения и среднего размера остатков, а также для других показателей, исчисляемых на определенные моменты времени
Слайд 71Средняя хронологическая
Если необходимо подсчитать среднюю для двух моментных показателей, то формула средней

хронологической превращается в формулу средней арифметической простой
Слайд 72Структурные средние
Обычно средней степенной для анализа распределения недостаточно.
Структурные средние применяются для первоначального

анализа распределения признаков в совокупности
Слайд 73Структурные средние
Из многочисленного множества структурных средних мы рассмотрим моду, медиану, квартиль, дециль

и перцентиль
Слайд 75Мода – значение признака, встречающееся в совокупности наибольшее число раз.
В быту

слово «мода» фактически имеет обратный смысл
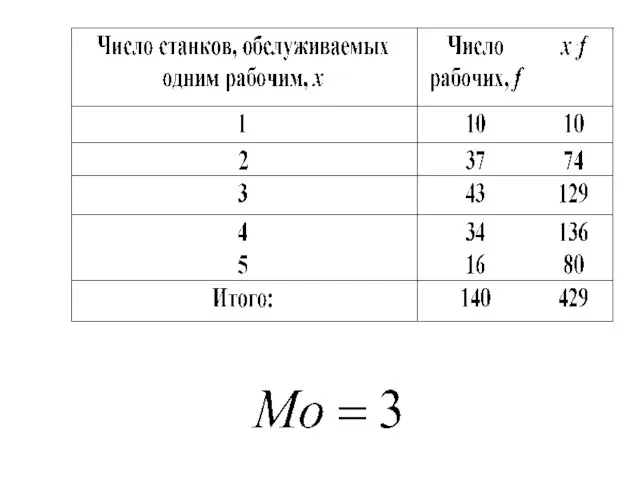
Слайд 76Мода – это наиболее часто встречающаяся варианта вариационного ряда.
Для дискретного ряда

это та варианта, которой соответствует наибольшая частота
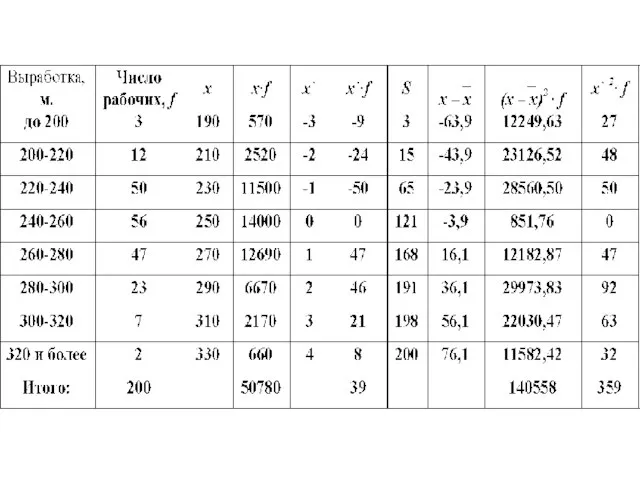
Слайд 78Для интервального ряда с равными интервалами мода определяется при помощи следующей формулы:

где xMо - начало модального интервала; hМо - величина модального интервала; f2 - частота модального интервала;
f1 - частота предмодального интервала; f3 - частота послемодального интервала
Слайд 81Мода
Если модальный интервал первый или последний, то недостающая частота (предмодальная или послемодальная)

берется равной нулю
Слайд 83Мода
В интервальном ряду как по формуле, так и графически мода вычисляется точнее

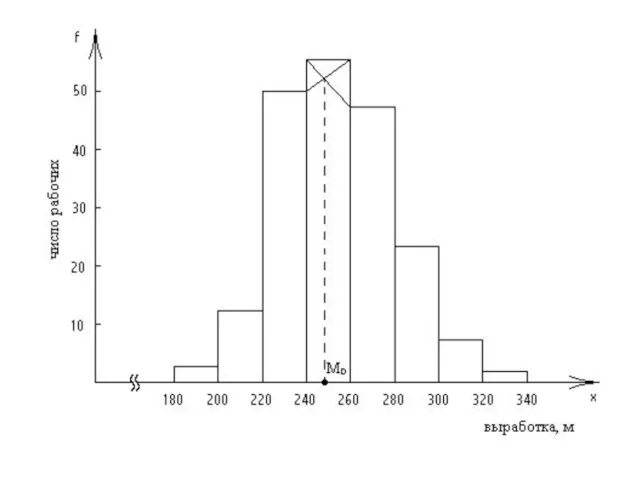
Слайд 84Мода
Для определения моды дискретного ряда строится полигон распределения. Расстояние от оси ординат

до наивысшей точки графика есть мода
Слайд 85Мода
Если в дискретном ряду несколько вариант имеют наибольшую частоту (что встречается достаточно

редко), то мода определяется как средняя арифметическая из всех модальных вариант
Слайд 87Медиана
Это центральное, серединное значение ряда. Ме - значение признака у единицы, находящейся

в середине ранжированной (упорядоченной) совокупности
Слайд 88Это варианта, лежащая в середине вариационного ряда и делящая его на две

равные части
Слайд 89Медиана
В дискретном ряду Ме находится по определению, а в интервальном ряду –

по формуле
Слайд 90Медиана
Если дискретный ряд содержит нечетное количество вариант, то находится та единственная варианта,

справа и слева от которой находится одинаковое число вариант:
Слайд 91Медиана
Если дискретный ряд содержит четное количество вариант, то находятся две варианты, справа

и слева от которых располагается одинаковое количество вариант. Ме равна средней арифметической из двух значений:
Слайд 92Для дискретного ряда медианой является та варианта, для которой накопленная частота впервые

превышает половину от суммы частот
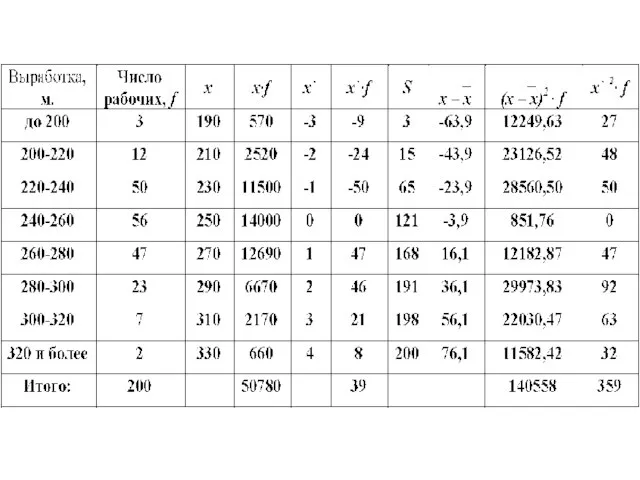
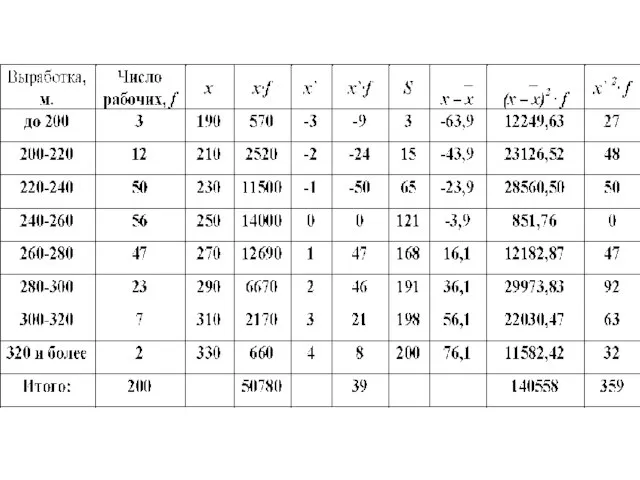
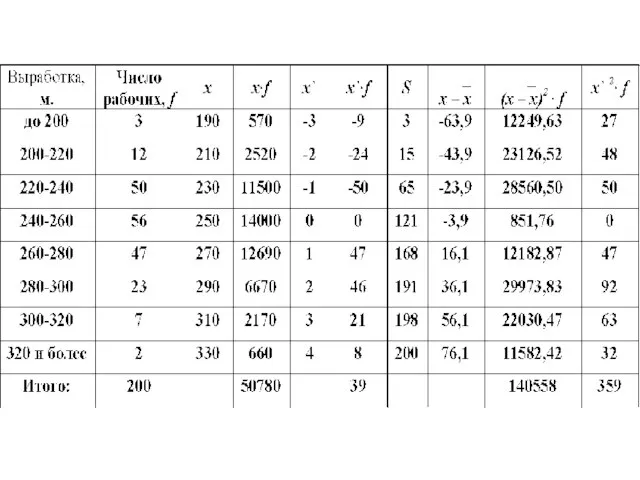
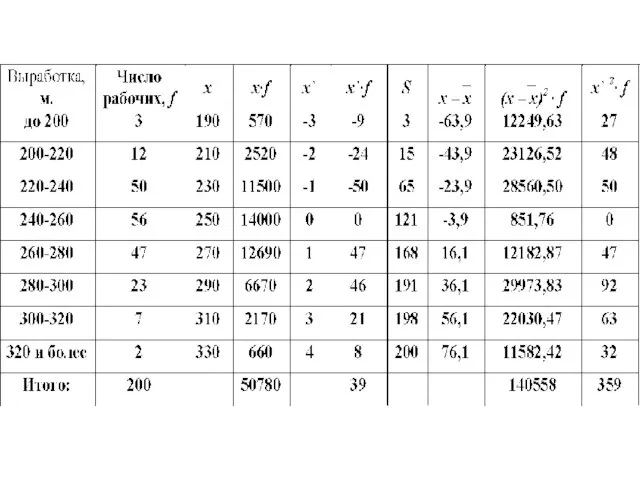
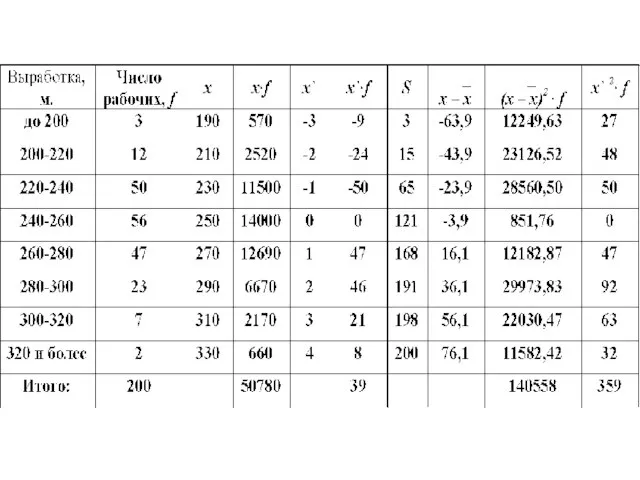
Слайд 94 Для интервального ряда медиана определяется по следующей формуле:
где xМе - начало

медианного интервала;
hМе - величина медианного интервала;
fМе - частота медианного интервала;
SМе-1 - накопленная частота предмедианного интервала
Слайд 96
Это означает, что у половины рабочих производительность труда меньше 252.5 м, а

у другой половины больше
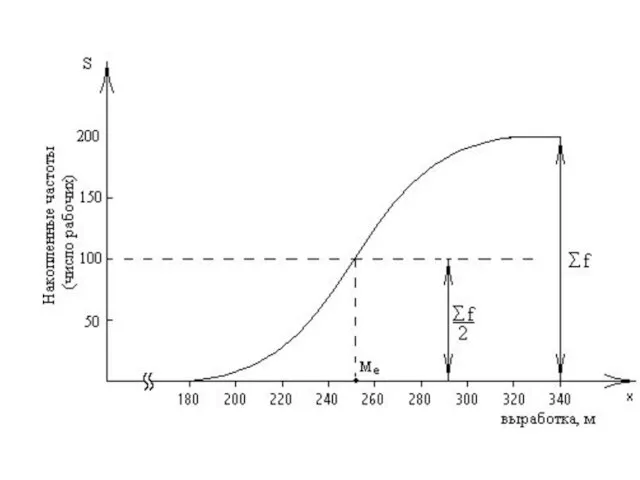
Слайд 97Для графического определения медианы последнюю ординату кумуляты делят пополам. Через полученную точку

проводят прямую, параллельную оси x до пересечения ее с кумулятой. Абсцисса точки пересечения является медианой представленного на графике распределения
Слайд 99Для графического определения медианы по огиве выполняют обратные действия, поскольку в огиве

накопленные частоты помещают на оси абсцисс, а значения признака – на оси ординат
Слайд 100Мо и Ме
В практических расчетах Мо и Ме могут быть величинами, далеко

отстоящими друг от друга. Для более четкой фиксации характера распределения используют другие структурные средние
Слайд 102Это варианты, которые делят ранжированную совокупность на четыре равные части:
Q1 1:3;
Q2 2:2

(Q2=Ме);
Q3 3:1
Слайд 103Квартили
Первый (нижний) квартиль отсекает от совокупности ¼ часть единиц с минимальными значениями,

а третий (верхний) отсекает ¼ часть единиц с максимальными значениями
Слайд 104Квартили
Мы как бы отбрасываем нетипичные, случайные значения признака. С помощью квартилей мы

определяем границы, где находятся 50% единиц, наиболее характерные для этой совокупности
Слайд 105Для расчета Q1 (первого квартиля) используется следующая формула:
где xQ1 - начало интервала,

содержащего 1-й квартиль;
hQ1 - величина интервала, содержащего 1-й квартиль;
SQ1 -1 - накопленная частота предшествующего интервала;
fQ1 - частота интервала, содержащего Q1
Слайд 106Интервалом, содержащим Q1, является тот интервал, для которого накопленная частота впервые превышает

¼ от суммы частот
Слайд 108
Это означает, что ¼ рабочих имеет производительность труда меньше, чем 234м., а

¾ имеет производительность труда больше
Слайд 110Для расчета Q3 используется формула:
Все обозначения аналогичны Q1 .
Интервалом, содержащим Q3 ,
является

тот интервал, для которого накопленная частота впервые превышает ¾ от суммы частот
Слайд 114Децили -
это варианты, которые делят ранжированную совокупность на 10 равных частей

Слайд 115Общая формула для расчета децилей:
где xDi - начало интервала,содержащего i-й дециль;
hDi

- величина интервала, содержащего i-й дециль;
fDi - частота интервала, содержащего Di;
SDi-1 - накопленная частота предшествующего интервала
Слайд 116Интервалом, содержащим Di ,является тот интервал, для которого накопленная частота впервые превышает

i/10 от суммы частот
Слайд 118Пример:
Это означает что, 60% рабочих имеют производительность труда меньше 259,6м, а 40%

- больше
Слайд 119Применение децилей
Пример - децильный коэффициент дифференциации населения. Население делится на 10 частей

по уровню дохода. Берут первые 10% и последние 10%. Считают, что средний доход последней группы не должен быть больше, чем в 10 раз среднего дохода первой группы. В России официально это превышение составляет 14-16 раз, неофициально – 20 и более раз
Слайд 120Перцентиль
П делит ранжированную совокупность на 100 равных частей. Формулы аналогичны формулам медианы,

квартиля и дециля
























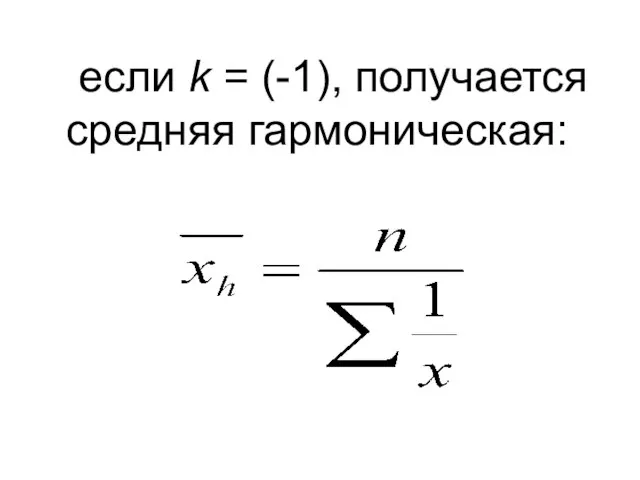








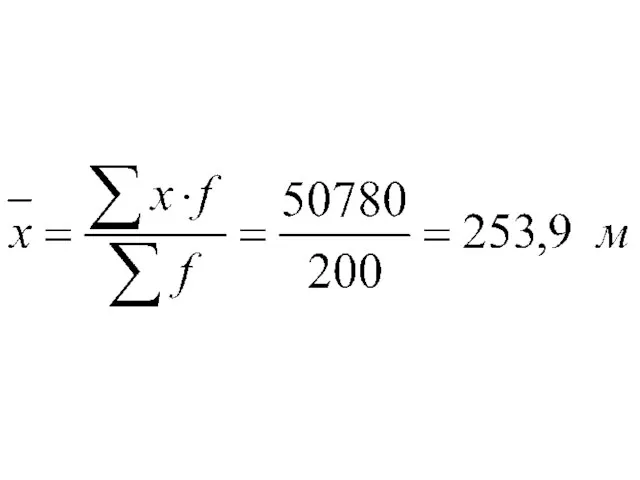

















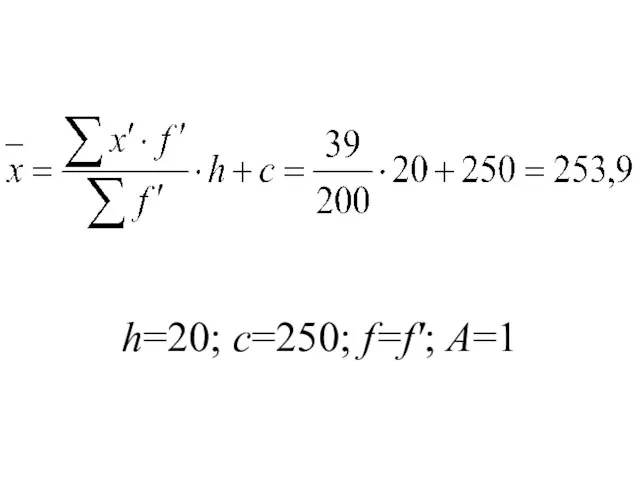



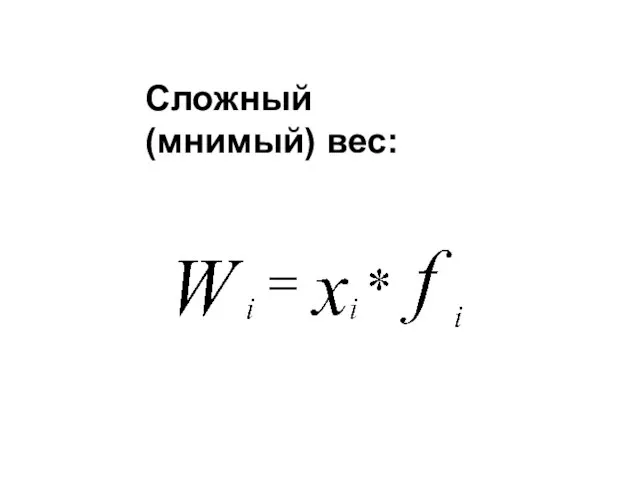



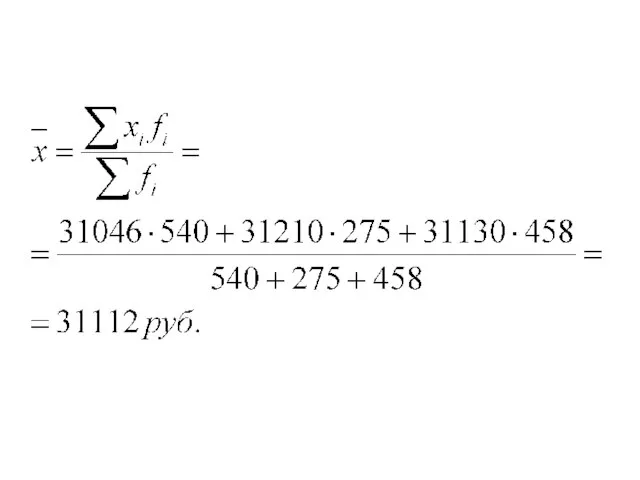
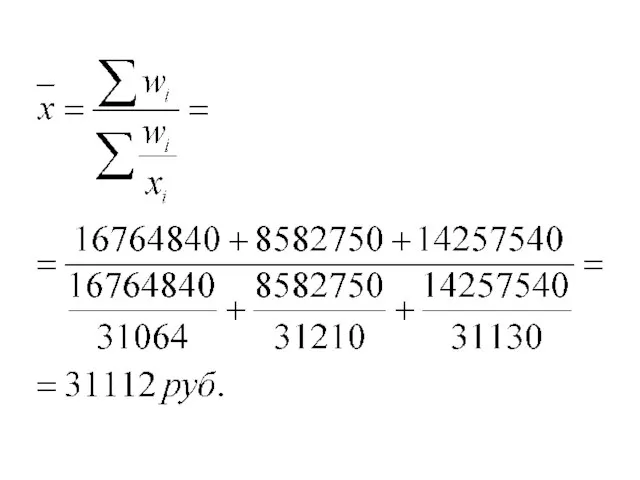










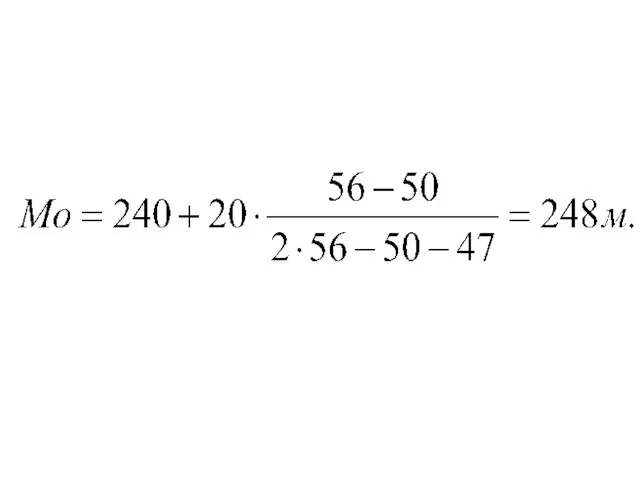

























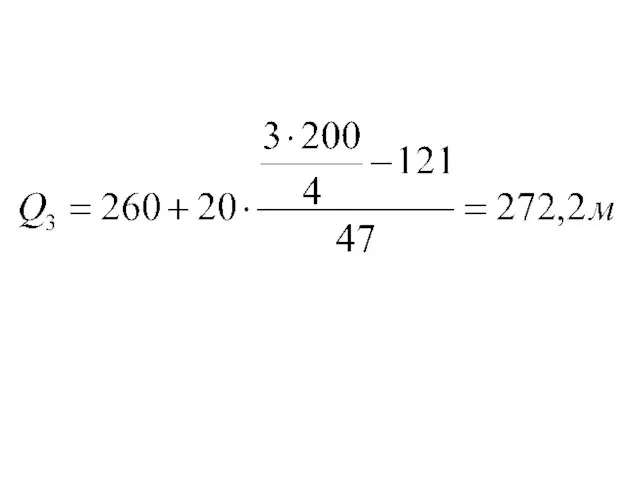







 Этапы принятия решения
Этапы принятия решения Викторина Iч 2022 26.10
Викторина Iч 2022 26.10 Режущий инструмент лущильных станков
Режущий инструмент лущильных станков Презентация на тему На пути к индустриальной эре
Презентация на тему На пути к индустриальной эре  Транспортно-пересадочные узлы в рамках реализации комплексного инвестиционного проекта «Реконструкция и развитиеМалого кольца
Транспортно-пересадочные узлы в рамках реализации комплексного инвестиционного проекта «Реконструкция и развитиеМалого кольца Презентация (2)
Презентация (2) Петрович. Моя корзина
Петрович. Моя корзина Бер өн менән генә айырылған һүҙҙәр уйла
Бер өн менән генә айырылған һүҙҙәр уйла Источники и системы теплоснабжения
Источники и системы теплоснабжения Природный стиль. Драма
Природный стиль. Драма Уильям Шекспир
Уильям Шекспир Как усовершенствовать учебную деятельность
Как усовершенствовать учебную деятельность Декларация о правах ребенка
Декларация о правах ребенка Ташкент – столица Узбекистана
Ташкент – столица Узбекистана История становления СПО НИКА УралГУФК
История становления СПО НИКА УралГУФК Месяц безопасности
Месяц безопасности Презентация на тему Родная природа в стихотворениях русских поэтов 19 века
Презентация на тему Родная природа в стихотворениях русских поэтов 19 века Рельеф Южной Америки
Рельеф Южной Америки Yarema Zyelyk
Yarema Zyelyk Еко-туризм в селі Дмитрівка, Одеській області
Еко-туризм в селі Дмитрівка, Одеській області Правила проведения аварийно-спасательных работ при обрушении зданий и сооружений
Правила проведения аварийно-спасательных работ при обрушении зданий и сооружений Карьера
Карьера Акционерный капитал
Акционерный капитал Стилистическая эволюция в творчестве Матиса Готхарта-Нитхарта
Стилистическая эволюция в творчестве Матиса Готхарта-Нитхарта ПРЕДВАРИТЕЛЬНЫЕ ИТОГИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКОГО РАЗВИТИЯ ОМСКОЙ ОБЛАСТИ В 2010 ГОДУ
ПРЕДВАРИТЕЛЬНЫЕ ИТОГИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКОГО РАЗВИТИЯ ОМСКОЙ ОБЛАСТИ В 2010 ГОДУ Самообразование педагога
Самообразование педагога Олимпийские игры. Где и когда проходили первые Олимпийские игры
Олимпийские игры. Где и когда проходили первые Олимпийские игры Таёжная область Северного Урала
Таёжная область Северного Урала