СТАНЦИЯ «ИСТОРИЧЕСКАЯ»

МАГИЧЕСКИЕ КВАДРАТЫ

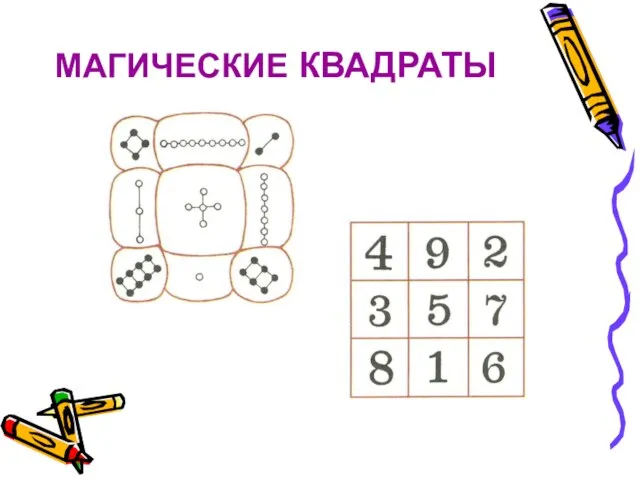
Порассуждаем
над построением магического квадрата.
Сумма всех чисел от 1 до 9 равна 45.
Всего в квадрате 3 строки. Значит, в каждой строке сумма чисел должна быть равна 45:3=15. Но тогда, чтобы квадрат был магическим, в каждом столбце и на каждой диагонали сумма чисел должна быть равна 15.
Выпишем все возможные представления числа 15 в виде суммы трех слагаемых от 1 до 9.
Заметим, что число, стоящее в центре таблицы должно встречаться в этих суммах 4 раза (столбец, строка, 2 диагонали). Каждое число, стоящее в углу таблицы, должно встречаться в суммах 3 раза (строка, столбец, диагональ). А число, стоящее на одном из оставшихся 4-х мест, должно встречаться в суммах только 2 раза (строка, столбец).
Так как в полученных суммах 4 раза встречается только число 5, оно и должно стоять в центре таблицы. Трижды встречаются в суммах числа 2, 4, 6 и 8. Значит, они должны стоять в углах таблицы, причем так, чтобы 2 и 8 были на одной диагонали (2 + 5 + 8 = 15), а 4 и 6 – на другой.
Продолжая рассуждения, можно построить данный магический квадрат.

ЗАДАНИЯ
Впишите в пустые клетки квадрата такие числа, чтобы квадрат стал магическим.
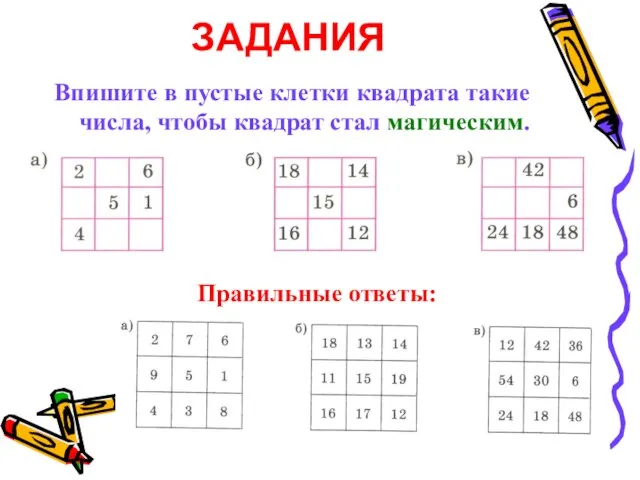
Правильные ответы: