Содержание
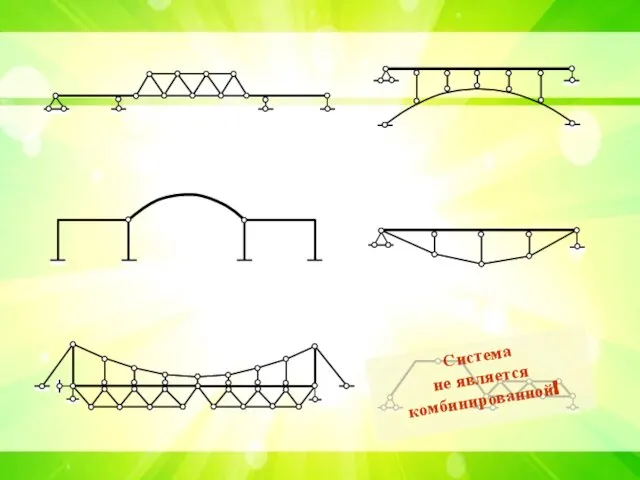
- 2. Комбинированной называется геометрически неизменяемая система, состоящая из различных по характеру своей работы частей, совместно участвующих в
- 3. Система не является комбинированной!
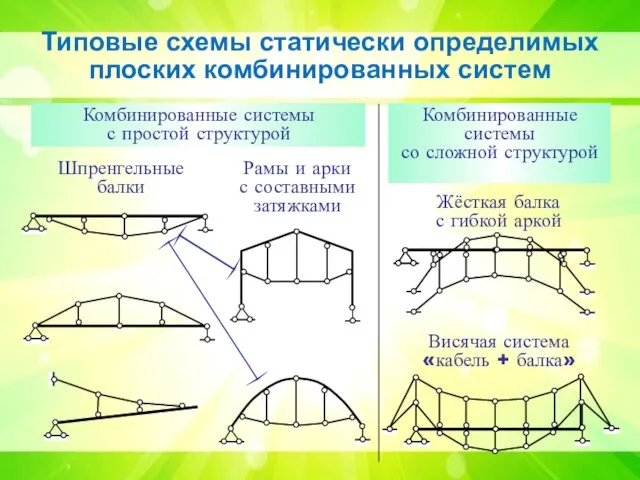
- 4. Типовые схемы статически определимых плоских комбинированных систем Шпренгельные балки Рамы и арки с составными затяжками Комбинированные
- 5. А В С 1 2 3 4 Структурный анализ А В С 1 2 3 4
- 6. А В С 1 2 3 4 Расчёт системы Порядок ш а г и – синтеза
- 7. А В С 1 2 3 4 Расчёт системы Порядок ш а г и – синтеза
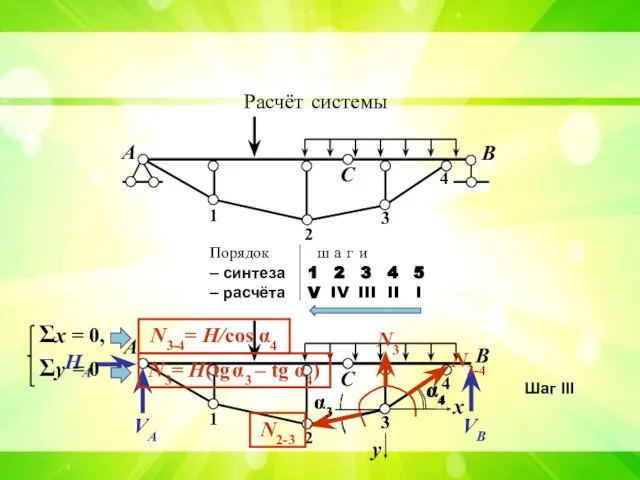
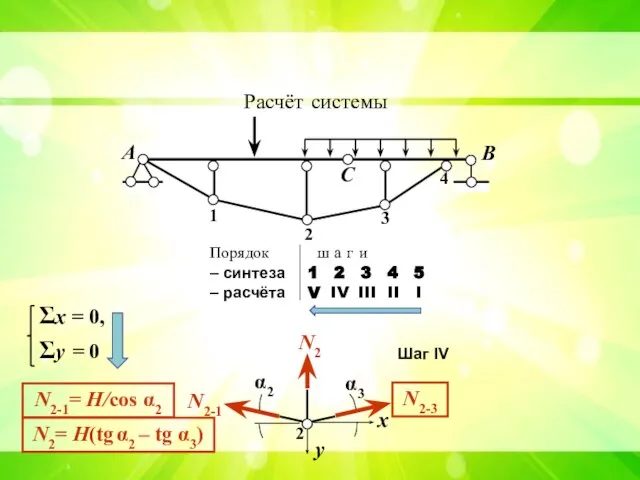
- 8. А В С 1 2 3 4 Расчёт системы Порядок ш а г и – синтеза
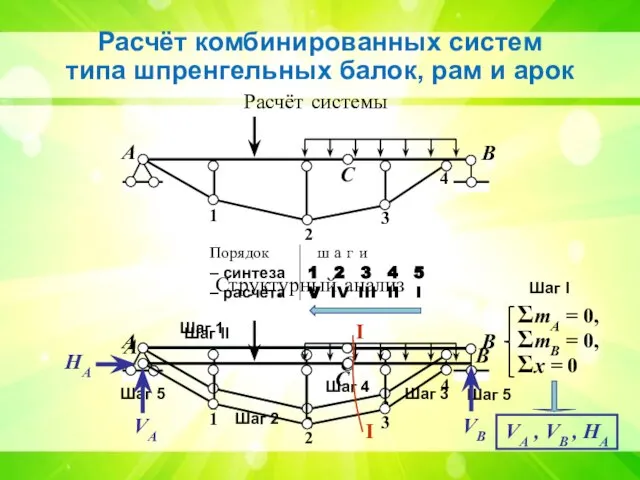
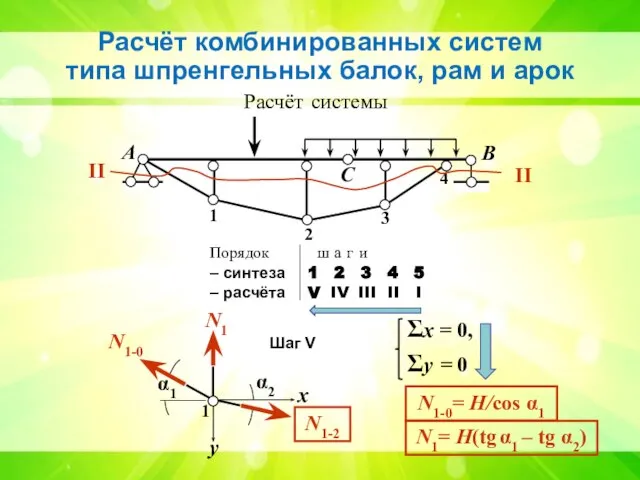
- 9. Расчёт комбинированных систем типа шпренгельных балок, рам и арок А В С 1 2 3 4
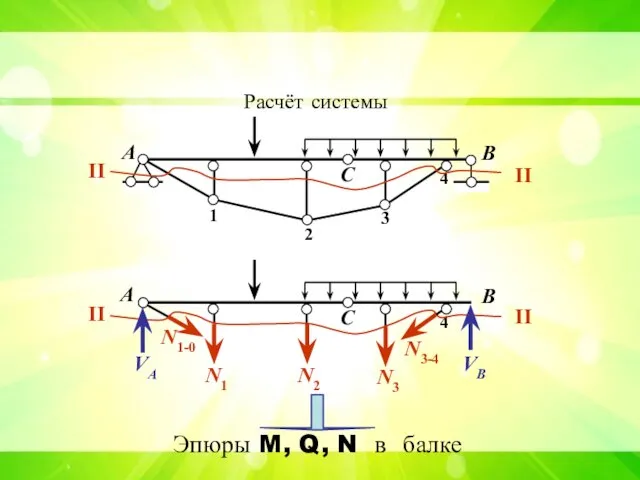
- 10. А В С 1 2 3 4 Расчёт системы II II А В С 4 II
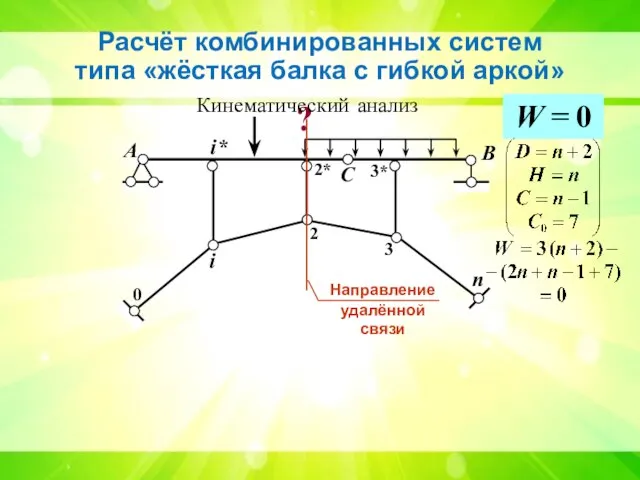
- 11. Расчёт комбинированных систем типа «жёсткая балка с гибкой аркой» А В С i 2 3 n
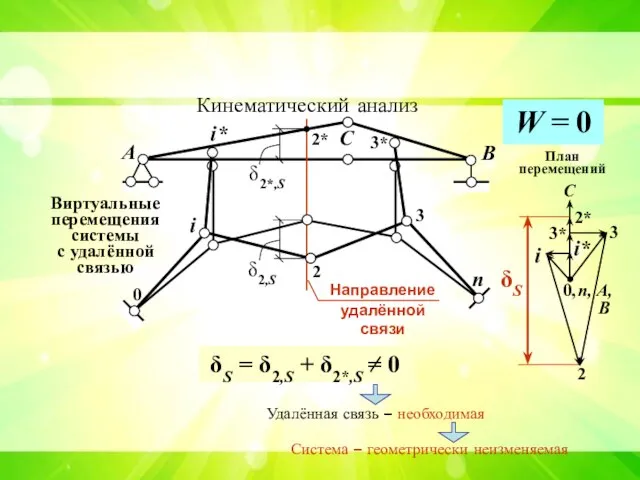
- 12. А В С Кинематический анализ i* 2* 3* i 2 3 n 0 Направление удалённой связи
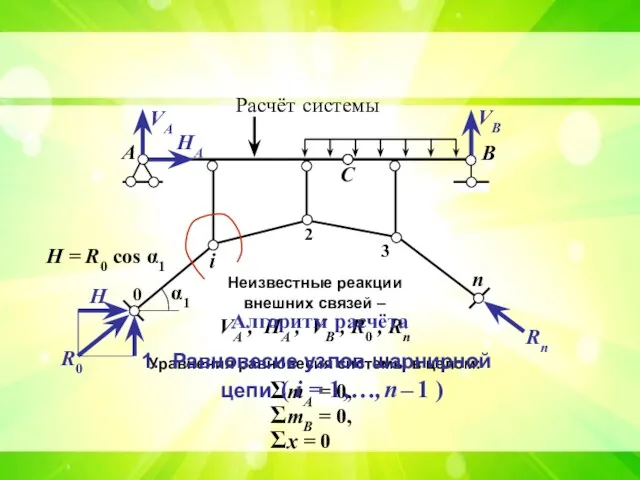
- 13. А В С i 2 3 n 0 Расчёт системы VА VВ R0 Rn HА H
- 14. i Расчёт системы αi αi+1 Ni-1, i Ni, i+1 N i y Алгоритм расчёта Равновесие узлов
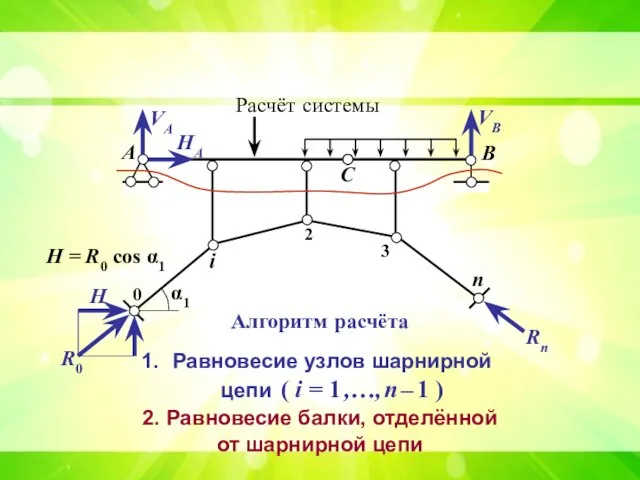
- 15. А В С i 2 3 n 0 Расчёт системы VА VВ R0 Rn HА H
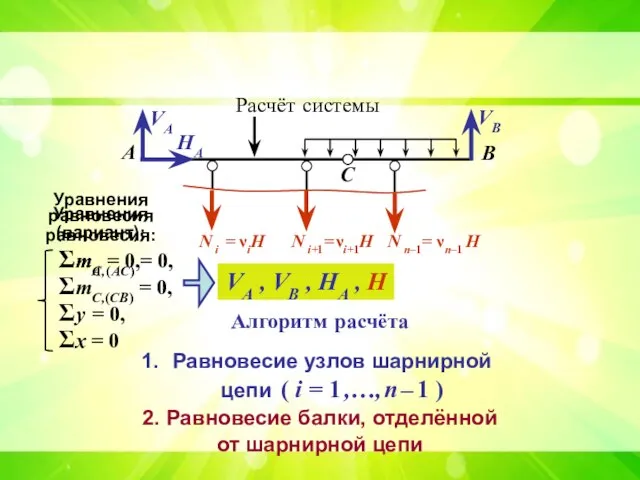
- 16. А В С Расчёт системы VА VВ HА Алгоритм расчёта Равновесие узлов шарнирной цепи ( i
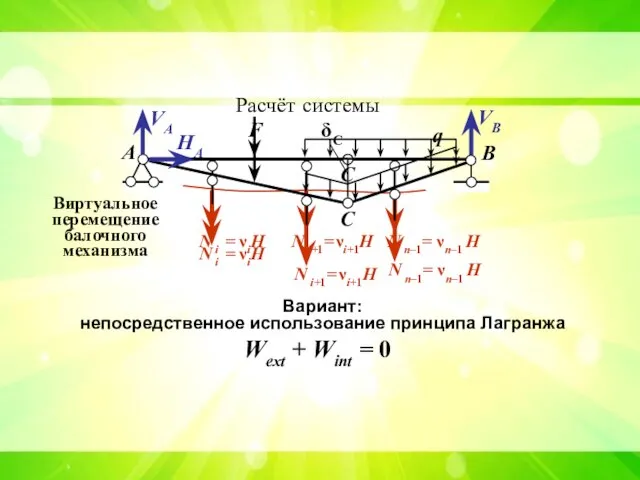
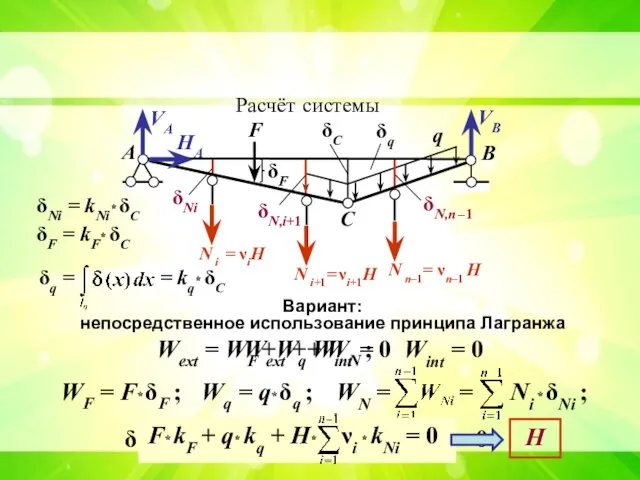
- 17. А В С Расчёт системы VА VВ HА Вариант: непосредственное использование принципа Лагранжа Wext + Wint
- 18. А В Расчёт системы VА VВ HА Вариант: непосредственное использование принципа Лагранжа Wext + Wint =
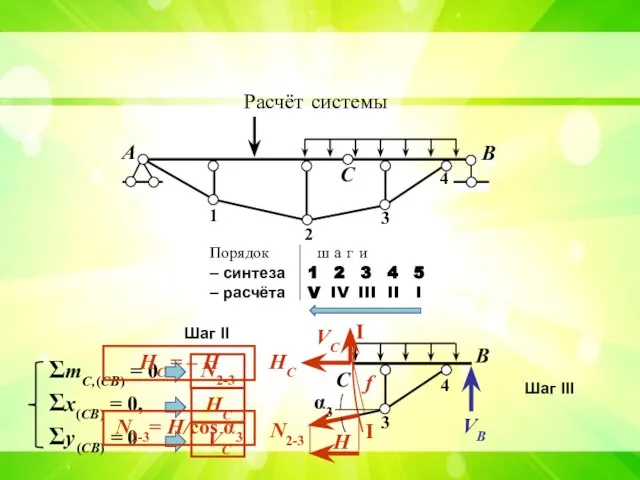
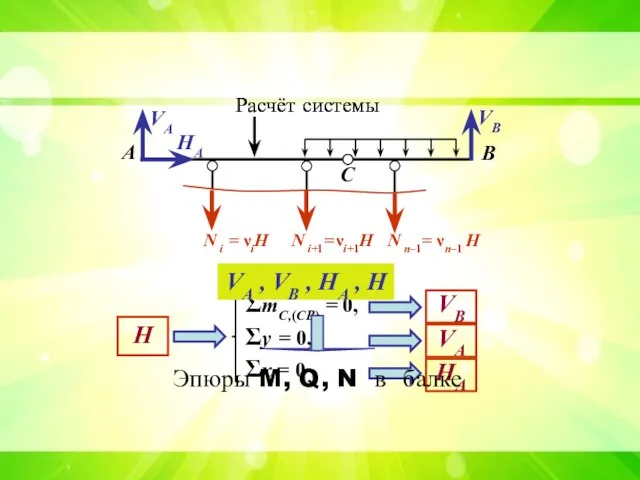
- 19. Расчет системы H ΣmC,(CB) = 0, Σy = 0, Σx = 0 VB VA HA Расчёт
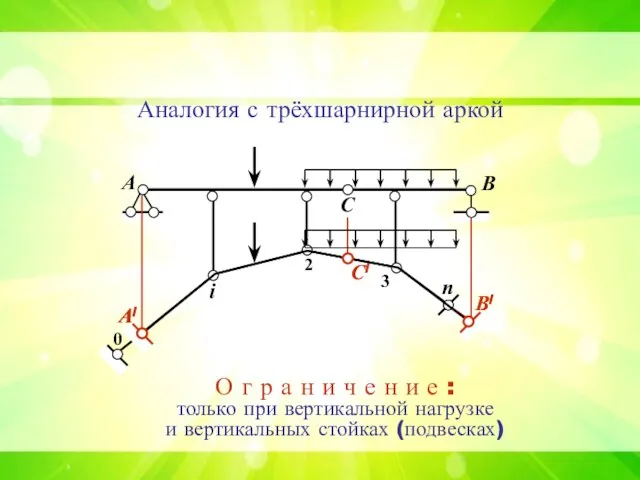
- 20. А В С i 2 3 n 0 Аналогия с трёхшарнирной аркой О г р а
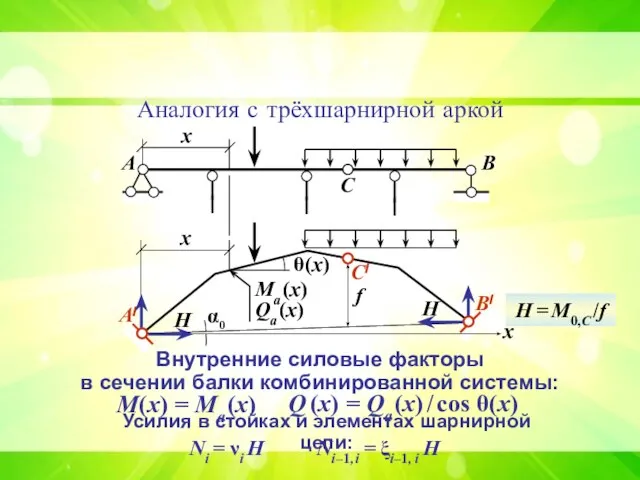
- 21. А/ B/ C/ Аналогия с трёхшарнирной аркой х θ(х) Qа (x) Mа (x) А В С
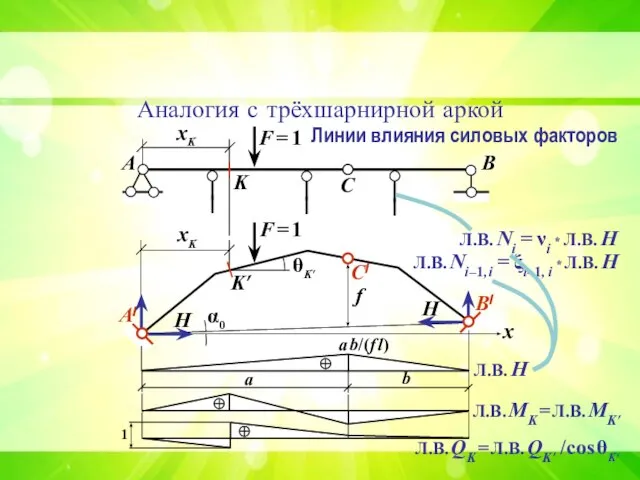
- 22. А/ B/ C/ Аналогия с трёхшарнирной аркой θK’ А В С хK х α0 H H
- 24. Скачать презентацию


 Легкая атлетика. Гладкий Бег
Легкая атлетика. Гладкий Бег Презентация на тему Организм и его свойства
Презентация на тему Организм и его свойства Темперамент
Темперамент Выражение художником своего отношения к изображаемому
Выражение художником своего отношения к изображаемому Алгоритмы и исполнители
Алгоритмы и исполнители … OVA - это принципиально новый проект от компании InVision, предлагающий возможность готовых решений по созданию сайта и его дальнейш
… OVA - это принципиально новый проект от компании InVision, предлагающий возможность готовых решений по созданию сайта и его дальнейш 4D-моделирование в строительной отрасли
4D-моделирование в строительной отрасли Мышление. Формы мышления
Мышление. Формы мышления Правила поведения в ситуациях, связанных с терроризмом
Правила поведения в ситуациях, связанных с терроризмом Презентация на тему Русская литература начала 20 века 11 класс
Презентация на тему Русская литература начала 20 века 11 класс  Исследование верхнего и нижнего течения реки Охта в Санкт-Петербурге.Начало исторического исследования.
Исследование верхнего и нижнего течения реки Охта в Санкт-Петербурге.Начало исторического исследования. Презентация на тему Урок рисования бабочки
Презентация на тему Урок рисования бабочки Arbat Street
Arbat Street Выход из тупика. Что делать когда уже ничего не хочется и ничего не радует
Выход из тупика. Что делать когда уже ничего не хочется и ничего не радует Кем быть и какими нам быть?
Кем быть и какими нам быть? Нормативно-документальное обеспечение сетевого взаимодействия в МАДОУ № 83
Нормативно-документальное обеспечение сетевого взаимодействия в МАДОУ № 83 Дни недели
Дни недели Non stop original
Non stop original Презентация на тему ПИНГВИНЫ
Презентация на тему ПИНГВИНЫ  Девушки бывают разные
Девушки бывают разные Нижегородский народный костюм
Нижегородский народный костюм Социальные сети
Социальные сети  Танцы ХХ века
Танцы ХХ века ОДАРЁННЫЕ ДЕТИ. УЧЕБНЫЙ АСПЕКТ.
ОДАРЁННЫЕ ДЕТИ. УЧЕБНЫЙ АСПЕКТ. Устройство настольного горизонтально-фрезерного станка
Устройство настольного горизонтально-фрезерного станка Обсадная колонна для надежной фиксации скважин
Обсадная колонна для надежной фиксации скважин Кризис трёх лет
Кризис трёх лет Космические фантазии
Космические фантазии