Статистические критерии (Непараметрические критерии)

Статистический критерий https://ru.wikipedia.org/wiki/Статистический_критерий
строгое математическое правило, по которому принимается или отвергается та или иная
статистическая гипотеза с известным уровнем значимости.
Построение критерия представляет собой выбор подходящей функции от результатов
наблюдений (ряда эмпирически полученных значений признака), которая служит для
выявления меры расхождения между эмпирическими значениями и гипотетическими.
Статистическая гипотеза https://ru.wikipedia.org/wiki/Проверка_статистических_гипотез
предположение о виде распределения и свойствах случайной величины, которое можно
подтвердить или опровергнуть применением статистических методов к данным выборки.
Пусть в (статистическом) эксперименте доступна наблюдению случайная величина X,
распределение которой P полностью или частично неизвестно. Тогда любое
утверждение, относительно , называется статистической гипотезой.
На практике обычно требуется проверить какую-то конкретную и как правило простую
гипотезу H0. Такую гипотезу принято называть нулевой. При этом параллельно
рассматривается противоречащая ей гипотеза H1, называемая конкурирующей или
альтернативной.
Статистические критерии. Введение

Этапы проверки статистических гипотез
1. Формулировка основной гипотезы H0 и конкурирующей гипотезы H1.
2. Задание уровень значимости α, на котором в дальнейшем и будет сделан вывод о справедливости гипотезы. Он равен вероятности допустить ошибку первого рода.
3. Расчёт статистики φ критерия такой, что:
- её величина зависит от исходной выборки
- по её значению можно делать выводы об истинности гипотезы H0;
- φ, как функция случайной величины X, также является случайной величиной и подчиняется какому-то закону распределения.
4. Построение критической области. Из области значений φ выделяется подмножество C таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство P(φ∈C)= α. Это множество C и называется критической областью.
5.Вывод об истинности гипотезы. Наблюдаемые значения выборки подставляются в статистику φ и по попаданию (или непопаданию) в критическую область C выносится решение об отвержении (или принятии) выдвинутой гипотезы H0.

Ошибки первого и второго рода https://ru.wikipedia.org/wiki/Ошибки_первого_и_второго_рода
Ошибки первого и второго рода являются взаимно-симметричными, то есть если поменять местами гипотезы H0 и H1, то ошибки первого рода превратятся в ошибки второго рода и наоборот.
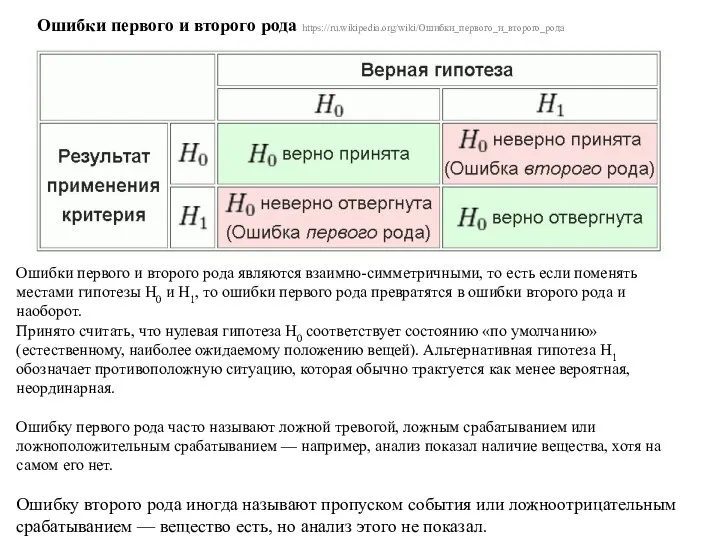
Принято считать, что нулевая гипотеза H0 соответствует состоянию «по умолчанию» (естественному, наиболее ожидаемому положению вещей). Альтернативная гипотеза H1 обозначает противоположную ситуацию, которая обычно трактуется как менее вероятная, неординарная.
Ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным срабатыванием — например, анализ показал наличие вещества, хотя на самом его нет.
Ошибку второго рода иногда называют пропуском события или ложноотрицательным
срабатыванием — вещество есть, но анализ этого не показал.

Вероятность ошибки первого рода при проверке статистических гипотез называют уровнем значимости и обычно обозначают греческой буквой α.
В статистических тестах обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением является уровень значимости, которым задаются при проверке статистических гипотез. Например, в случае металлодетектора повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а понижение чувствительности — к увеличению риска ошибки второго рода (пропуск запрещённого предмета).
Статистическая значимость https://ru.wikipedia.org/wiki/Статистическая_значимость
В статистике величину называют статистически значимой, если мала вероятность её случайного возникновения или ещё более крайних величин. Здесь под крайностью понимается степень отклонения тестовой статистики от нуль-гипотезы.
Уровень α значимости теста — вероятность отклонить гипотезу H, если на самом деле она верна (решение известное как ошибка первого рода, или ложноположительное решение).
Популярными уровнями значимости являются 10 %, 5 %, 1 %, и 0,1 %.
Различные значения α -уровня имеют свои достоинства и недостатки.
Меньшие α -уровни дают большую уверенность в том, что уже установленная альтернативная гипотеза значима, но при этом есть больший риск не отвергнуть ложную нулевую гипотезу (ошибка второго рода, или «ложноотрицательное решение»).
Выбор α -уровня неизбежно требует компромисса между следовательно между вероятностями ошибок первого и второго рода.

Виды статистических критериев https://ru.wikipedia.org/wiki/Статистический_критерий
Критерии значимости. Проверка на значимость предполагает проверку гипотезы о численных
значениях известного закона распределения:
H0: a=a0 — нулевая гипотеза. H1: a>a0 (a
Критерии согласия. Проверка на согласие подразумевает проверку предположения о том, что
исследуемая случайная величина подчиняется предполагаемому закону. Критерии согласия можно
также воспринимать, как критерии значимости. Критериями согласия являются:
Критерий Пирсона
Критерий Колмогорова
Критерии проверки на однородность. При проверке на однородность случайные величины
исследуются на факт значимости различия их законов распределения (т.е. проверки того,
подчиняются ли эти величины одному и тому же закону).
Это разделение условно, и один и тот же критерий может быть использован в разных качествах.
- - -
Непараметрические критерии - группа статистических критериев, которые не включают в расчёт
параметры вероятностного распределения и основаны на оперировании частотами или рангами.
[Критерий Уилкоксона, Критерий Пирсона (или критерий согласия χ2 (Хи-квадрат) ,
Критерий Колмогорова-Смирнова]
Непараметрические критерии - группа статистических критериев, которые включают в расчёт
параметры вероятностного распределения (средние и дисперсии).
[t-критерий Стьюдента, Критерий Фишера]

КРИТЕРИЙ χ2 (Критерий согласия Пирсона)
На практике часто приходится встречаться с задачами следующего рода.
Некоторое испытание производится несколько раз, причем известна теоретическая
частота появления некоторого события при этом испытании.
Однако на практике фактическая частота оказалась несколько отличной от теоретической.
Надо установить, можно ли объяснить имевшее место расхождение между частотами
случайными причинами
Пусть, например, известно, что процент брака при выпуске некоторой продукции в
среднем равен а.
Если среди выпускаемой продукции процент брака окажется равным b ≠ а, то можно ли
это расхождение объяснить случайными причинами или это расхождение существенно и
вызвано улучшением или ухудшением технологии производства этой продукции?
Для решения этого вопроса поступают следующим образом.
Построим некоторую величину, которую можно было бы принять за меру расхождения
между фактической и теоретической частотой. Эту величину называют критерием
значимости.
Определим вероятность того, что в силу случайных величин, критерий значимости примет
значения, равные или большие того значения, которое получено из опыта.

Если эта вероятность окажется малой, следовательно, достигнуто это значения не в силу
случайных причин и расхождение между теоретической и фактической частотами
существенно.
(Малая вероятность - расхождение неслучайно)
Если же эта вероятность окажется большой, то расхождение между теоретической и
фактической частотами следует признать случайным.
(Вероятность большая - расхождение случайно)
Вопрос о том, какую вероятность нужно считать малой, не может быть решен методами
математики; он зависит от характера рассматриваемой задачи. Часто при решении
подобных вопросов вероятность считают малой, если она меньше 0,05 (пятипроцентный
уровень значимости). Однако следует иметь в виду, что при этом в одном из каждых 20
случаев мы будем утверждать наличие эффекта, не существующего в действительности.
Если такой процент ошибки считается слишком большим, следует принять более высокий,
например, 1%-й уровень значимости.
Если нам нужно определить, случайно ли отличается частота появления некоторого
события от ожидаемого значения, то применяют так называемый χ2 критерий.

где Ф — фактически полученное значение частоты; Е — ожидаемая частота.
Суммирование производится по всем исходам опыта.
Не рекомендуется применять критерий χ2 в тех случаях, когда какое-либо Е меньше 5.
После того, как величина χ2 найдена, нужно из таблицы величины χ2 определить
вероятность того, что в силу случайных причин χ2 примет значение, равное или большее
того, которое найдено из опыта.
Таблица функции χ2 составлена по двум аргументам. Одним из них является вероятность
р, а другим — так называемое «число степеней свободы». Под числом степеней свободы
понимают число классов, значения которых можно задать произвольно.
Иными словами, это есть общее число классов минус число ограничений, наложенных на
изучаемую систему.
Если найденная по таблице вероятность мала (например, меньше 0,5 или меньше 0,1), то
расхождение между опытной и теоретической частотами неслучайно.
Критерий χ2 применяется также и при сравнении опытных частот, полученных в
результате нескольких опытов.
За меру расхождения между теоретической и наблюдаемой частотой принимают число:

Вероятности p
в долях 1.
Для получения в %
умножить на 100.

Создать файл в Exсel: Фамилия_МСС_Пр03
Задача 1
Прочность предмета испытывается с помощью стального шарика, который падает на
предмет с определенной высоты.
В одной серии испытанию подвергались 10 предметов, причем 5 из них были разбиты,
в другой серии из 20 предметов другого состава не выдержали испытания 14.
Можно ли считать, что прочность предмета обусловливается различием состава или
же различие в результатах опытов по сериям объясняется случайными причинами?
Подсказка
0. В расчетах дробных величин сохранять 2 знака после запятой
1. Вычислить общее (по обоим сериям) число разбитых (R) и целых предметов (Z).
R = R1+ R2, Z = Z1+ Z2,
где
R1 - число разбитых предметов в первой серии, Z1 - целых предметов в первой серии
R2 - число разбитых предметов во второй серии, Z2 - целых предметов во второй серии
2. Рассчитать общее (по обоим сериям) теоретические вероятности для предметов
PR быть разбитыми или PZ уцелеть как
PR=R/(R+Z), PZ=Z/(R+Z),
3. Найти теоретическое число разбитых предметов в 1 и 2 сериях
NR1= PR* N1, NR2= PR* N2,
(N1 - число предметов в первой серии, N2 - число предметов во второй серии)
4. Найти теоретическое число целых предметов в 1 и 2 сериях
NZ1= PZ* N1, NZ2= PZ* N2

4. Найти критерий χ2
Суммирование производится по всем исходам опыта:
всего 4 исхода опыта:
1) разбитое в первой серии, 2) уцелевшее в первой серии,
3) разбитое во второй серии, 2) уцелевшее во второй серии
5. Определить число степеней свободы
- Число степеней свободы находится как число классов, значения которых могут быть заданы произвольно. В нашем случае имеем всего два класса — класс разбитых и класс уцелевших предметов; однако произвольно мы можем задать численность только одного из них, а численность второго класса вычисляется.
6. Обращаясь к таблице «Критерий χ2» для нужного числа степеней свободы, находим, что какова вероятность нашей гипотезы.
- Если эта вероятность мала, то можно утверждать, что здесь имеется различие свойств испытываемого состава предмета.
- Если эта вероятность не мала, то нельзя утверждать, что здесь имеется различие свойств испытываемого состава предмета.
Ф — фактически полученное
значение частоты (число
предметов);
Е — ожидаемая частота (число
предметов).

Задача 2
В первой выборке в N1 изделий было R1 случаев брака; в другой выборке в N2 изделий было R2 случаев брака. Оправдывается ли с достаточной уверенностью предположение, что совокупности, представляемые этими двумя партиями, различны?
Подсказка
Решать аналогично задаче 1. Данные брать в МCC_Пр03_Распределение (...).xls
Задача 3
Выпуск сверхплановой продукции по сменам (в условных единицах): A, В, С
Можно ли считать расхождение в сверхплановом выпуске по сменам случайным?
Подсказка
Найти средний выпуск по сменам E
Ф — фактически полученное значение частоты (число предметов);
Е — ожидаемая частота (число предметов).
Данные брать в МCC_Пр03_Распределение (...).xls

Задача 4
В таблице (см. МCC_Пр03_Распределение (...).xls) приведены данные о процессе
работы машины. Испытывались четыре различных режима работы.
Проверить гипотезу, что частота поломок не зависит от метода загрузки
Подсказка
1) Вычислить общее количество циклов и общее количество поломок
2) Вычислить общую теоретическую (ожидаемую) частоту поломок по всем циклам
(число поломок на цикл)
3) Вычислить ожидаемое число поломок в каждом цикле
4) Вычислить на основании полученных данных χ2
5) Определить число степеней свободы
6) По таблице определить для найденного числа степеней свободы и χ2 вероятность.
7) Записать вывод: есть ли связь режима работы и поломок
Задача 5
При отсчетах по шкалам измерительных приборов последние цифры показаний обычно
оцениваются лишь приблизительно в долях деления шкалы.
При этом часто можно отметить предпочтение, которое даже опытные наблюдатели
оказывают одним цифрам перед другими.
В таблице (см. МCC_Пр03_Распределение (...).xls) приведено распределение NNN
случаев оценки последней цифры одним из наблюдателей при отсчете по
измерительному прибору в долях деления шкалы.
Имеем мы здесь дело с систематической ошибкой в отсчете или нет?