Содержание
- 2. (С) Веденяпин Е.Н. 2012 Основная литература Красс М.С., Чупрынов Б.П. «Математика для экономистов», СПб., Питер, 2007
- 3. (С) Веденяпин Е.Н. 2012 1. Анализ рисков Рассматриваемые вопросы: Выбор с помощью дерева решений Мера риска
- 4. (С) Веденяпин Е.Н. 2012 1.1. Выбор с помощью дерева решений Основные понятия методов анализа риска Любая
- 5. (С) Веденяпин Е.Н. 2012 Игры, в которых задается последовательность принятия решений игроками, называются позиционными играми. Число
- 6. (С) Веденяпин Е.Н. 2012 Позиционную игру наглядно представляет дерево решений (в общем случае — граф решений),
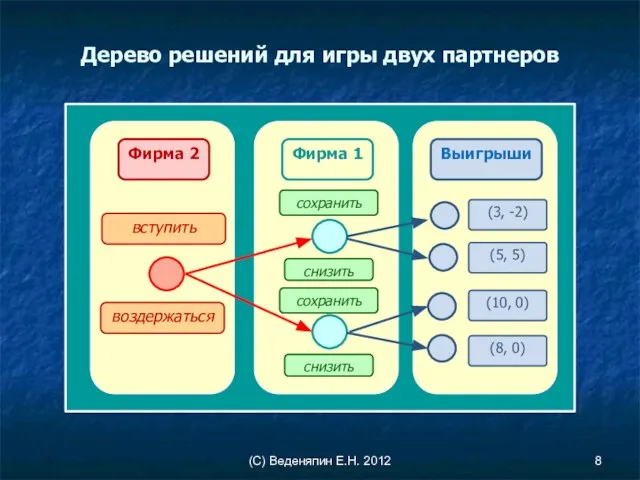
- 7. (С) Веденяпин Е.Н. 2012 На рынке доминирует производитель — фирма 1, и монопольное положение приносит ей
- 8. (С) Веденяпин Е.Н. 2012 Дерево решений для игры двух партнеров
- 9. (С) Веденяпин Е.Н. 2012 1. Формулировка задачи. Состоит в формализации экономического объекта и выбора основных определяющих
- 10. (С) Веденяпин Е.Н. 2012 Пример проведения процедуры принятия решения Администрация компании решает вопрос об инвестировании. Можно
- 11. (С) Веденяпин Е.Н. 2012 Пример проведения процедуры принятия решения (продолжение) Этапы 1-3 выполнены. Этап 4. Построение
- 12. (С) Веденяпин Е.Н. 2012 Пример проведения процедуры принятия решения (окончание) Этап 5. Проведение расчетов Ожидаемая прибыль
- 13. (С) Веденяпин Е.Н. 2012 Принятие решения при уточнении исходных данных Администрация компании решила потратить 10 000
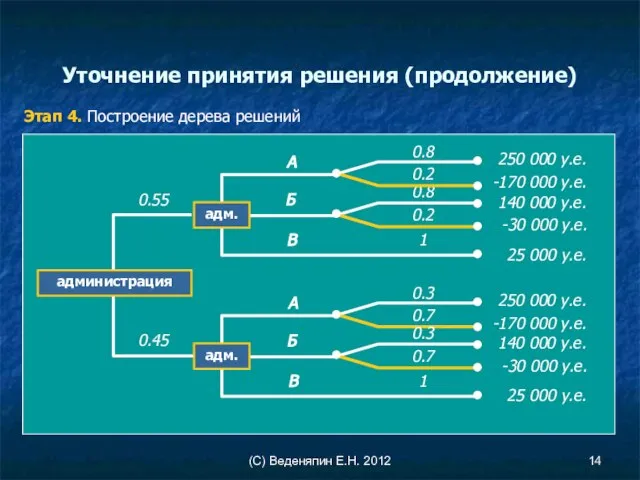
- 14. (С) Веденяпин Е.Н. 2012 Уточнение принятия решения (продолжение) Этап 4. Построение дерева решений
- 15. (С) Веденяпин Е.Н. 2012 Уточнение принятия решения (окончание) Благоприятный прогноз Неблагоприятный прогноз ВЫВОД: Если администрация склоняется
- 16. (С) Веденяпин Е.Н. 2012 Риск – это угроза потери действующим финансовым лицом части своих ресурсов, либо
- 17. (С) Веденяпин Е.Н. 2012 Замечание 1: На практике для оценки риска используется безразмерная величина риска Замечание
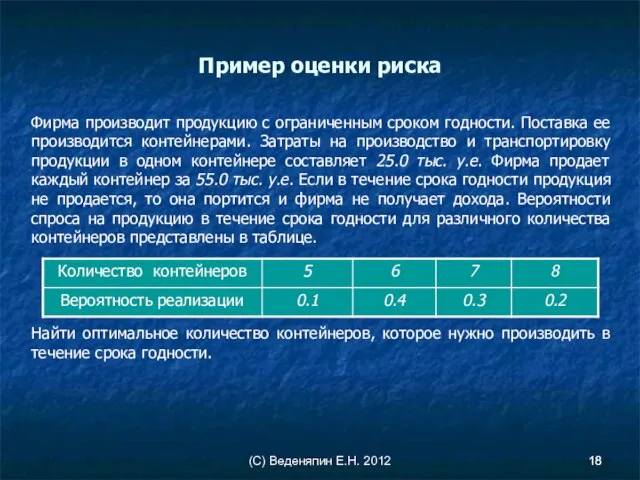
- 18. (С) Веденяпин Е.Н. 2012 Пример оценки риска Фирма производит продукцию с ограниченным сроком годности. Поставка ее
- 19. (С) Веденяпин Е.Н. 2012 Пример оценки риска (решение) Прибыль от каждого проданного контейнера 55.0-25.0=30.0 у.е. Убыток
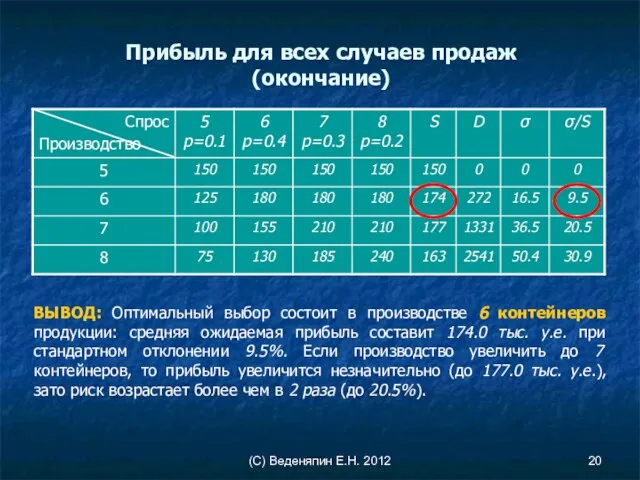
- 20. (С) Веденяпин Е.Н. 2012 Прибыль для всех случаев продаж (окончание) ВЫВОД: Оптимальный выбор состоит в производстве
- 21. (С) Веденяпин Е.Н. 2012 1.3. Основы портфельного анализа Поскольку ценные бумаги различаются по доходности и надежности,
- 22. (С) Веденяпин Е.Н. 2012 Линии безразличия Функция полезности – это функция, зависящая от ожидаемой доходности rp
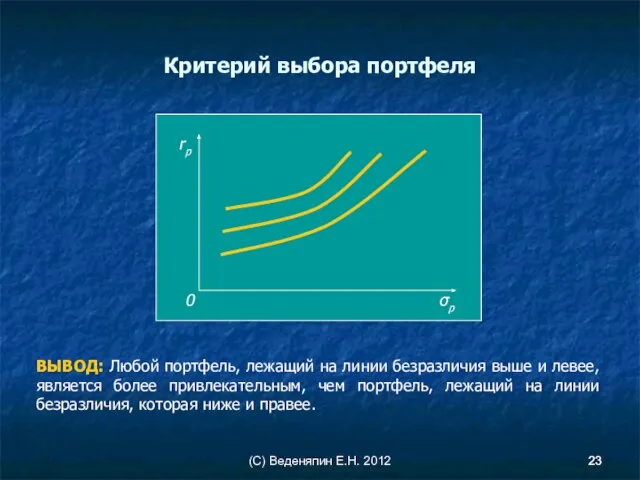
- 23. (С) Веденяпин Е.Н. 2012 Критерий выбора портфеля ВЫВОД: Любой портфель, лежащий на линии безразличия выше и
- 24. (С) Веденяпин Е.Н. 2012 Ожидаемая доходность портфеля хi – доля начальной стоимости портфеля, инвестированная в i-тый
- 25. (С) Веденяпин Е.Н. 2012 Дисперсия доходности портфеля Среднее квадратическое отклонение доходности портфеля
- 26. (С) Веденяпин Е.Н. 2012 Пример расчета доходности и риска портфеля Найти ожидаемую доходность и стандартное отклонение
- 27. (С) Веденяпин Е.Н. 2012 Диверсификация инвестиционного портфеля Свойство инвестиционного портфеля ценных бумаг обладать меньшим риском, чем
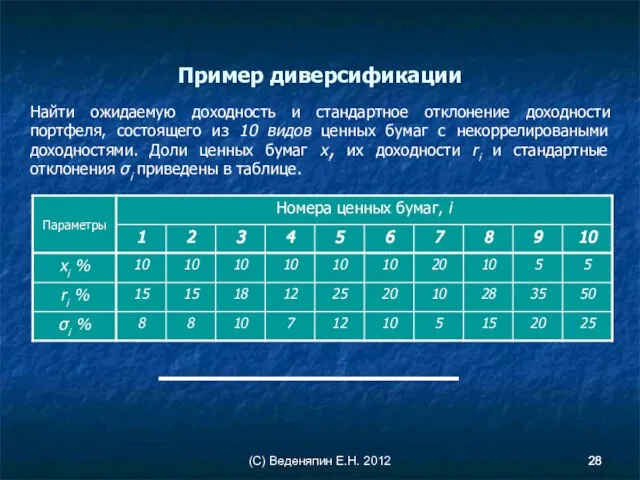
- 28. (С) Веденяпин Е.Н. 2012 Пример диверсификации Найти ожидаемую доходность и стандартное отклонение доходности портфеля, состоящего из
- 29. (С) Веденяпин Е.Н. 2012 Решение примера Ожидаемая доходность Дисперсия доходности Стандартное отклонение ВЫВОД: Крупные инвестиции позволяют
- 30. (С) Веденяпин Е.Н. 2012 1.4. Выбор оптимального портфеля Достижимое множество инвестиционных портфелей – это совокупность всех
- 31. (С) Веденяпин Е.Н. 2012 Инвестор выбирает оптимальный портфель из такого множества портфеля, каждый из которых: максимизирует
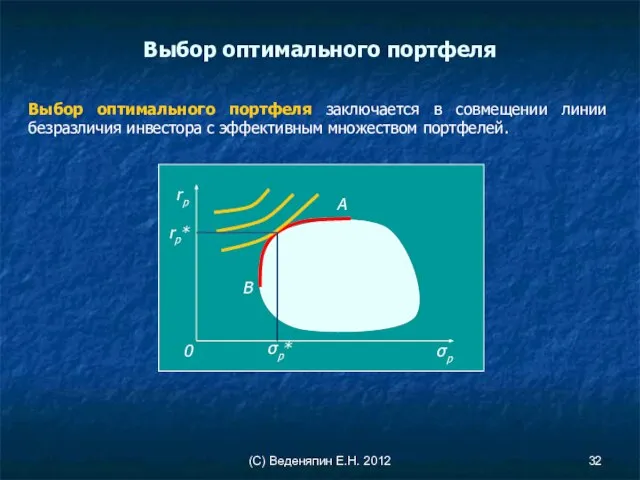
- 32. (С) Веденяпин Е.Н. 2012 Выбор оптимального портфеля заключается в совмещении линии безразличия инвестора с эффективным множеством
- 33. (С) Веденяпин Е.Н. 2012 Замечание: Выбор оптимального портфеля существенно зависит от формы линий безразличия, которая зависит
- 35. Скачать презентацию

























 Искусство папьемаше
Искусство папьемаше Задачи и содержание коррекционной и образовательной деятельности
Задачи и содержание коррекционной и образовательной деятельности Open TS: архитектура и реализация среды для динамического распараллеливания вычислений
Open TS: архитектура и реализация среды для динамического распараллеливания вычислений Программа банкета Gold party к Новому году
Программа банкета Gold party к Новому году Шоколад
Шоколад ПНП_1
ПНП_1 Торт Весна
Торт Весна Тема: «Подвижные игры для дошкольников».
Тема: «Подвижные игры для дошкольников». Комбинаторика. Комбинаторное правило умножения
Комбинаторика. Комбинаторное правило умножения УМК Перспектива
УМК Перспектива Что такое экономика? 6 класс
Что такое экономика? 6 класс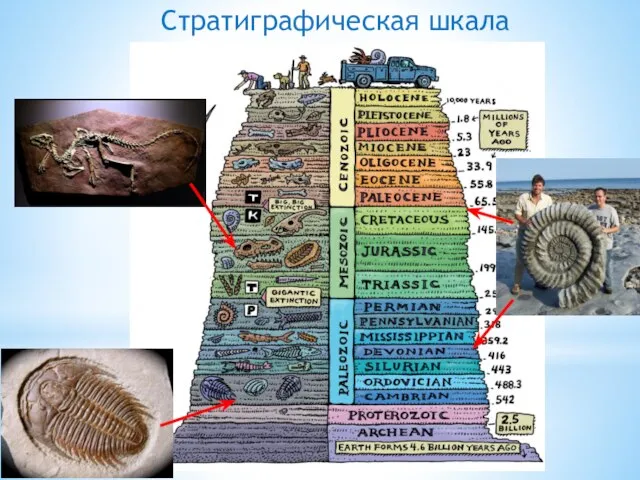 Стратиграфическая шкала
Стратиграфическая шкала Family Law
Family Law Изготовление хронограммы спортивного упражнения
Изготовление хронограммы спортивного упражнения Кровь. Переливание крови
Кровь. Переливание крови Суровые испытания лета - осени 1941 года Алтухова Кристина 8 «В» класс
Суровые испытания лета - осени 1941 года Алтухова Кристина 8 «В» класс КРЕАТИВНОЕ АГЕНСТВОMEDIAVAN
КРЕАТИВНОЕ АГЕНСТВОMEDIAVAN Нематериальные активы. Ресурсное обеспечение деятельности хозяйствующего субъекта
Нематериальные активы. Ресурсное обеспечение деятельности хозяйствующего субъекта Промоутер. Его задачи
Промоутер. Его задачи АВТОМАТИЗАЦИЯ МЕТРОЛОГИЧЕСКИХ СЛУЖБ
АВТОМАТИЗАЦИЯ МЕТРОЛОГИЧЕСКИХ СЛУЖБ Туристское снаряжение. Основные туристские узлы
Туристское снаряжение. Основные туристские узлы ПЫЛЕСОС.ТЕХНИКА БУДУЩЕГО
ПЫЛЕСОС.ТЕХНИКА БУДУЩЕГО Взаимодействие семьи и школы в современных условиях
Взаимодействие семьи и школы в современных условиях Справедливая торговля
Справедливая торговля Назначение и боевые свойства автомата Калашникова.
Назначение и боевые свойства автомата Калашникова. Познавательные процессы: внимание и память
Познавательные процессы: внимание и память Автоматизация слогослияния
Автоматизация слогослияния  Купаты ТМ «БАРСКИЙ СТОЛ» Продукт абсолютно натуральный, не содержит красителей и консервантов. Купаты - это вид сырых колбасок, нуж
Купаты ТМ «БАРСКИЙ СТОЛ» Продукт абсолютно натуральный, не содержит красителей и консервантов. Купаты - это вид сырых колбасок, нуж