Содержание
- 2. Статистический показатель Это количественная характеристика социально-экономического явления или процесса в условиях качественной определенности. Качественная определенность показателя
- 3. Статистический показатель Абсолютные Относительные Средние
- 4. Абсолютный показатель отражает физические размеры изучаемого явления именованный измеряются в конкретных единицах может быть положительным или
- 5. Абсолютный показатель Натуральные Стоимостные Трудовые Индивидуальные Суммарный Моментный Интервальный
- 6. Относительный показатель обобщающий показатель, который дает числовую меру соотношения двух сопоставляемых абсолютных величин и определяется как
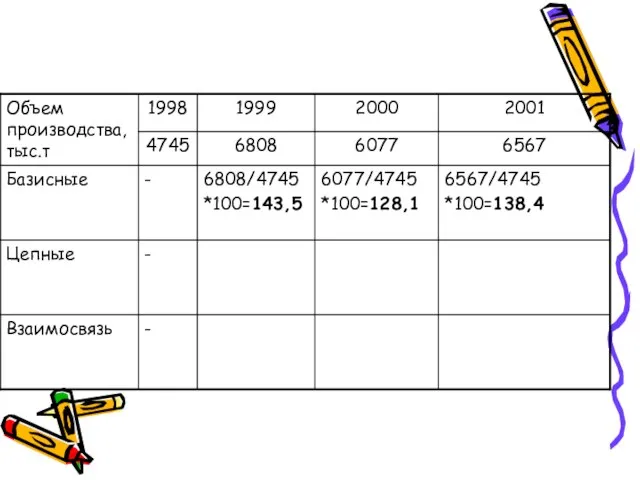
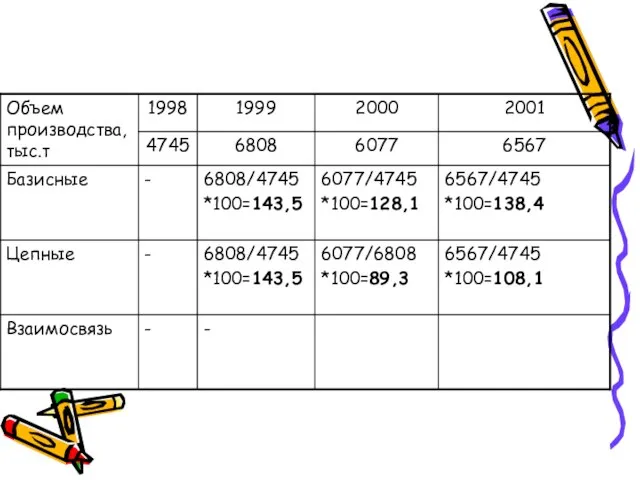
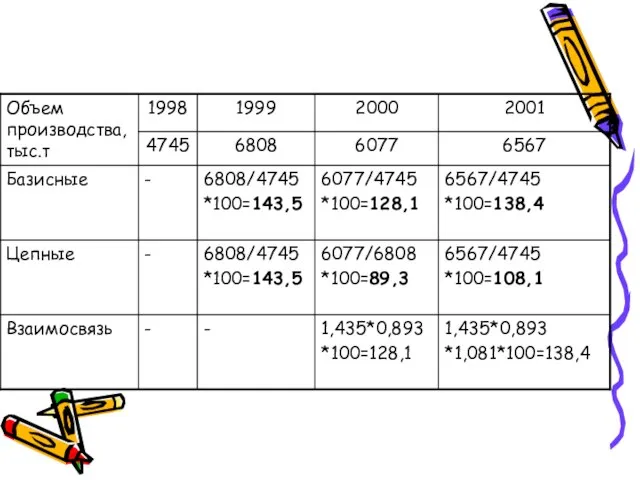
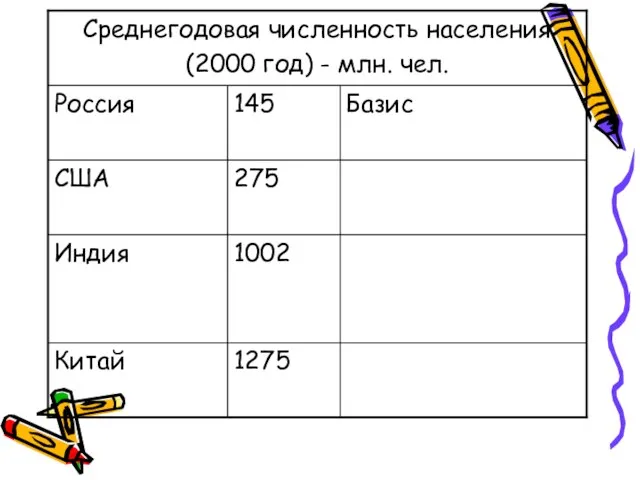
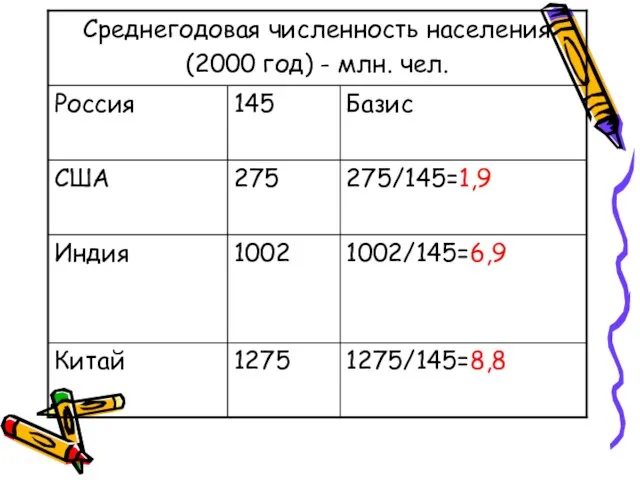
- 7. Цепной относительный показатель – если база сравнения переменная Базисный относительный показатель – если база сравнения постоянная
- 8. Относительный показатель
- 9. Относительный показатель динамики – темп роста Характеризует изменение уровня развития какого-либо явления во времени
- 14. Относительный показатель выполнения плана и планового задания ; . ОПП*ОПРП=ОПД относительные показатели плана относительные показатели реализации
- 15. Оборот торговой фирмы в 2002 г. составил 2,0 млн. руб. На 2003 год запланировано достичь оборота
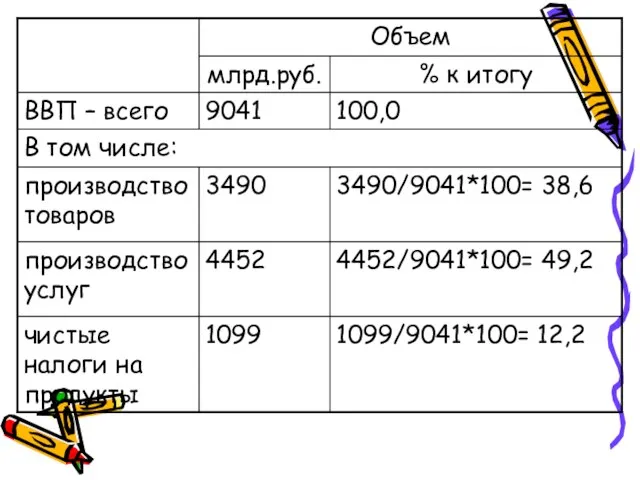
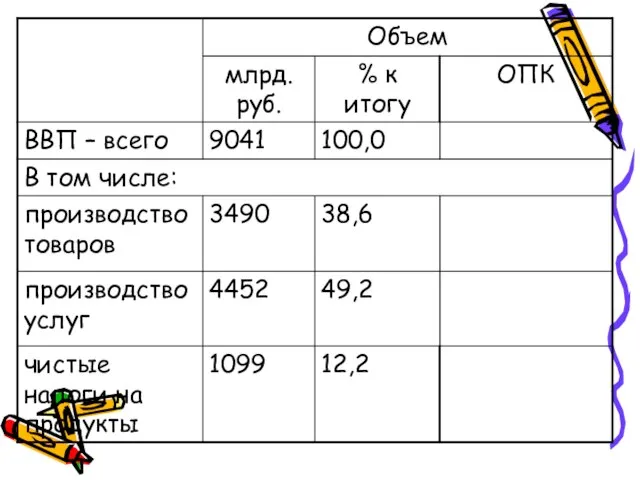
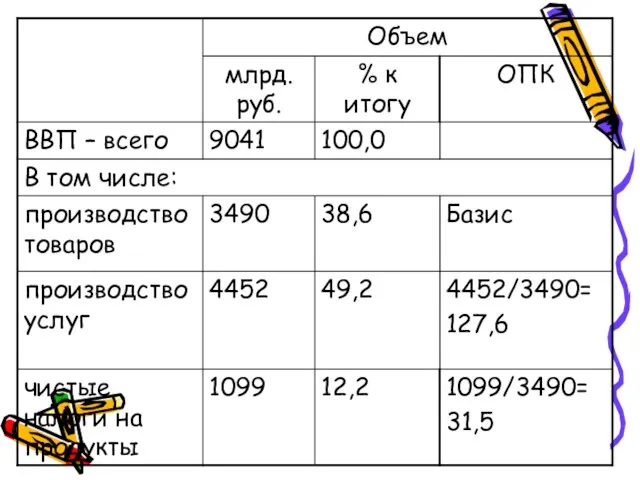
- 16. Относительные величины структуры Характеризуют доли, удельные веса составных элементов в общем итоге
- 19. Относительный показатель координации Характеризует отношение частей данной совокупности к одной из них, принятой за базу сравнения
- 22. Относительный показатель сравнения Характеризует сравнительные размеры одноименных абсолютных величин, относящихся к одному и тому же периоду
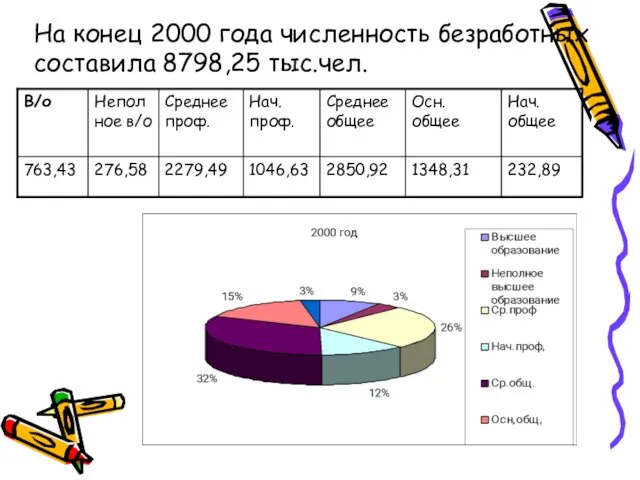
- 25. Относительный показатель интенсивности Характеризует степень распределения или развития данного явления в той или иной среде
- 26. На конец 2000 года численность безработных составила 8798,25 тыс.чел.
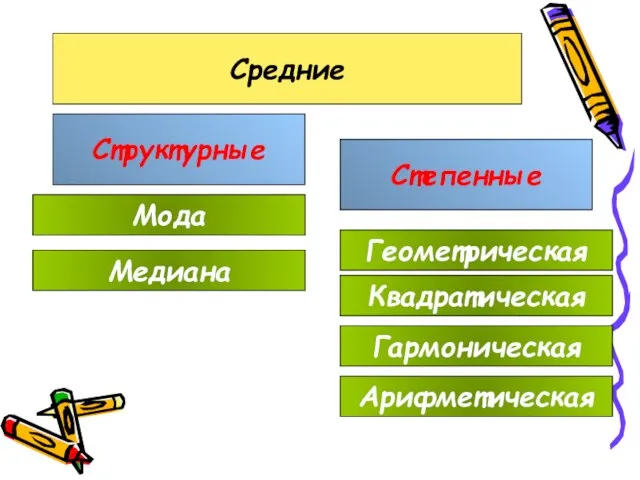
- 27. Средний показатель обобщающий показатель, характеризующий типический уровень явления
- 28. Средние Степенные Структурные Арифметическая Гармоническая Геометрическая Мода Квадратическая Медиана
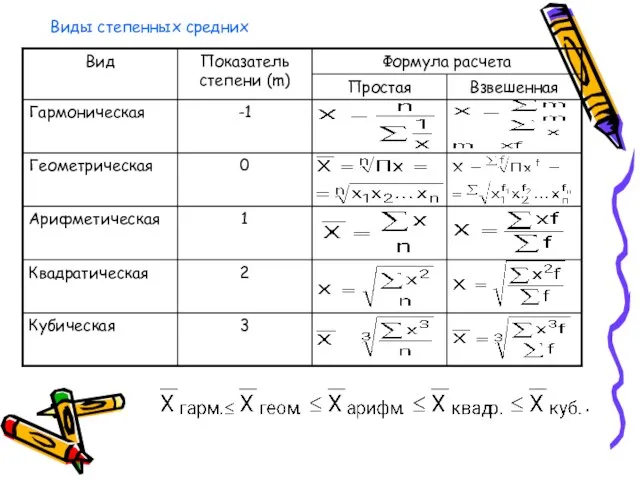
- 29. Степенные средние Простая средняя где Xi - варианта (значение) осредняемого признака; m - показатель степени средней;
- 30. Виды степенных средних
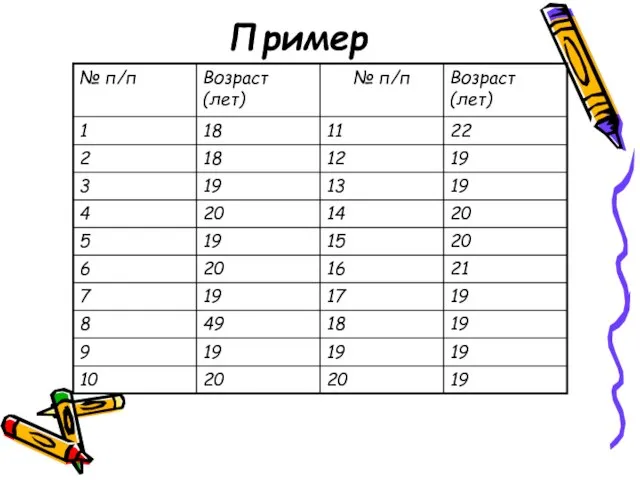
- 31. Пример
- 32. Средний возраст Простая средняя Взвешенная средняя
- 33. Структурные средние Мода наиболее часто повторяющееся значения признака где ХMo - нижнее значение модального интервала; mMo
- 34. Структурные средние Медиана величина признака, которая делит упорядоченную последовательность его значений на две равные по численности
- 35. Показатели вариации: частотные показатели; показатели распределения – структурные средние; показатели степени вариации; показатели формы распределения.
- 36. Частотные показатели вариации абсолютная численность i-той группы – частота fi относительная частота – частость di кумулятивная
- 37. Показатели вариации:
- 38. Показатели вариации:
- 39. Дисперсия: Дисперсия постоянной величины равна 0. Если все значения вариантов признака X уменьшить на постоянную величину
- 40. Показатели относительного рассеивания :
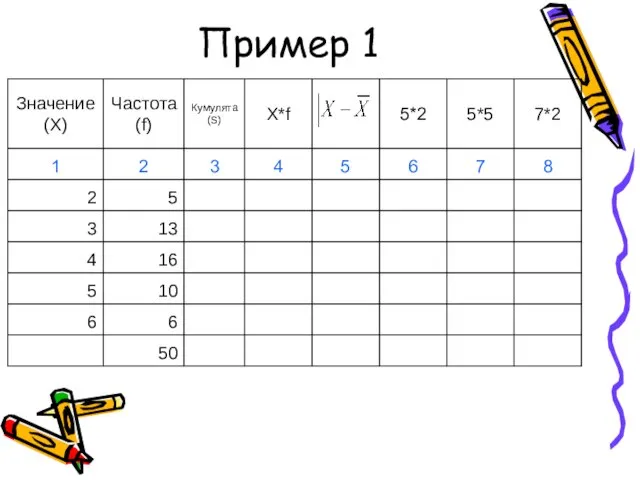
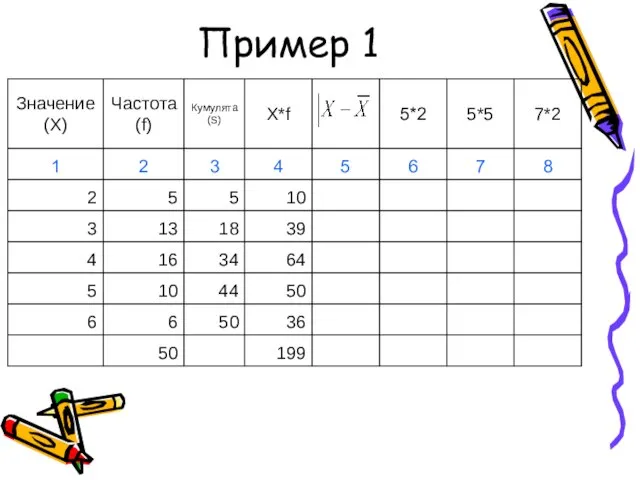
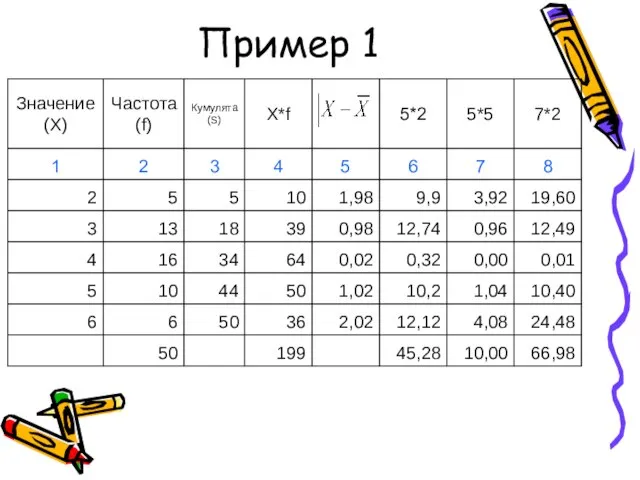
- 41. Пример 1
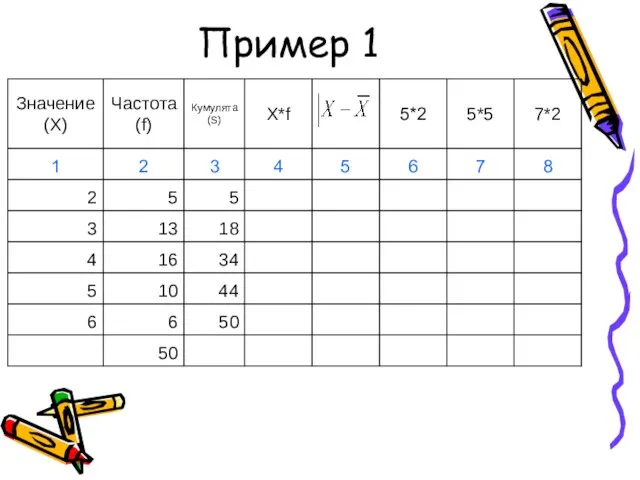
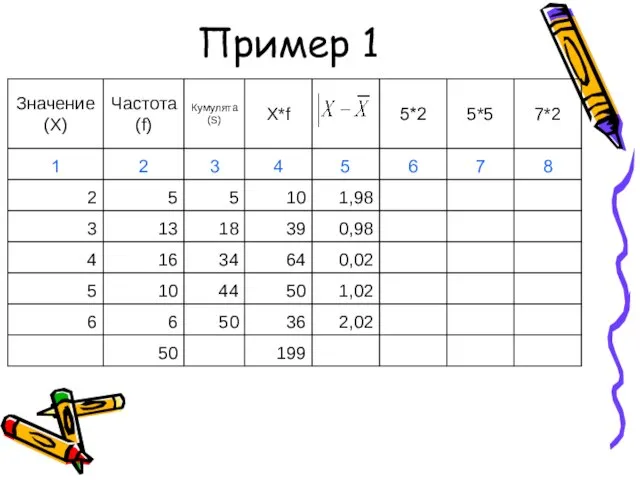
- 42. Пример 1
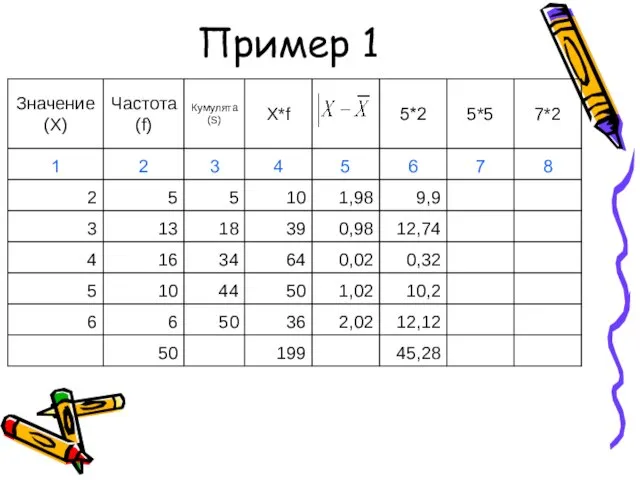
- 43. Пример 1
- 44. Пример 1
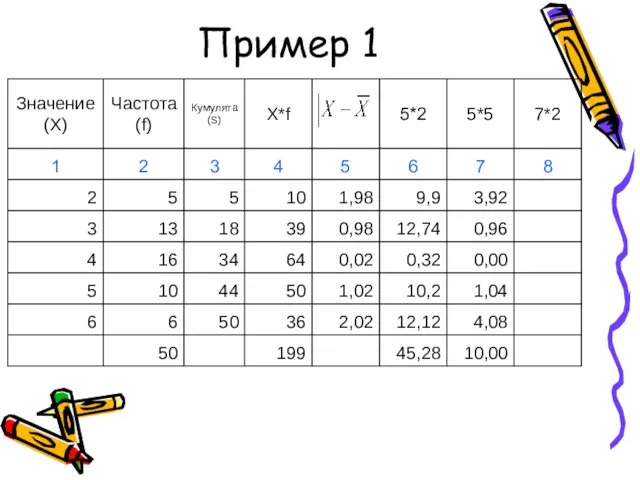
- 45. Пример 1
- 46. Пример 1
- 47. Пример 1
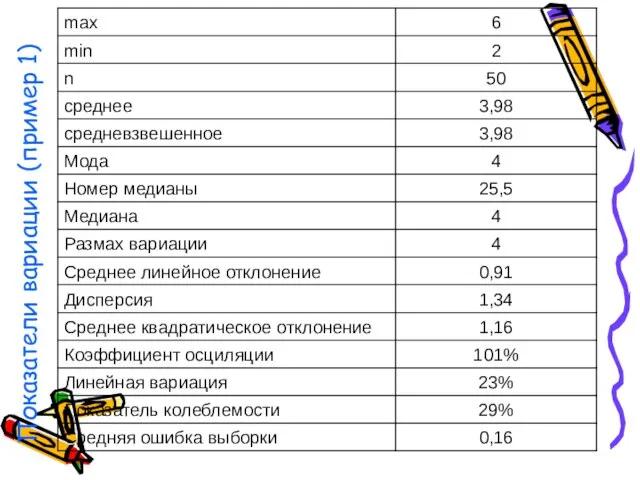
- 48. Показатели вариации (пример 1)
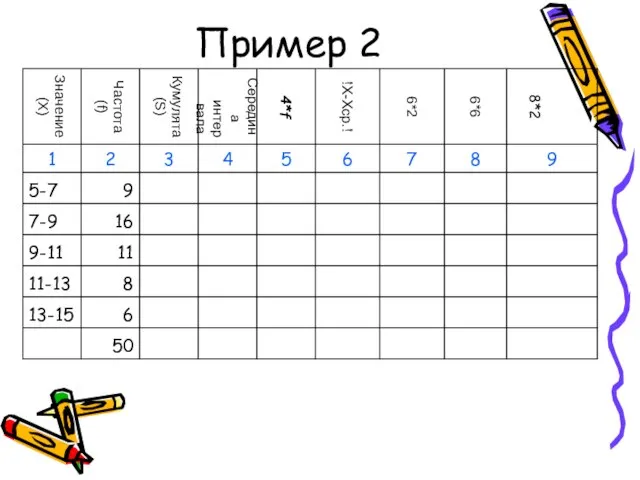
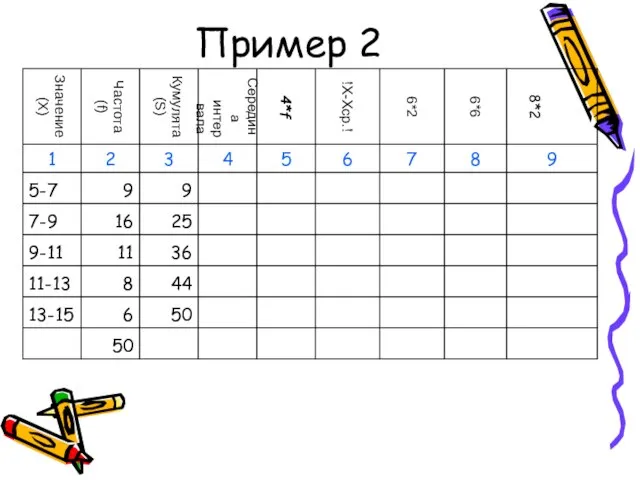
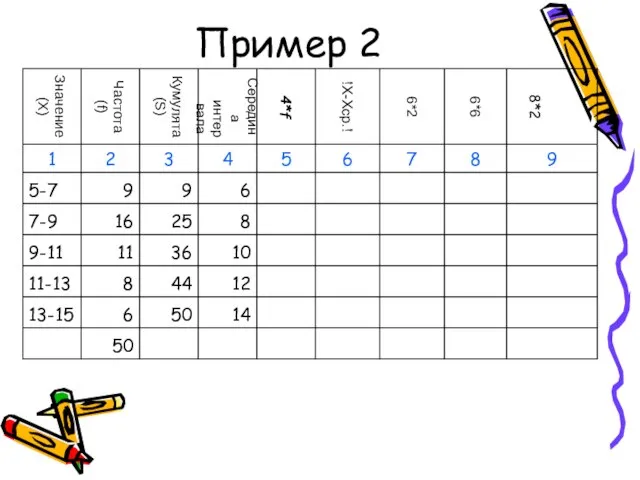
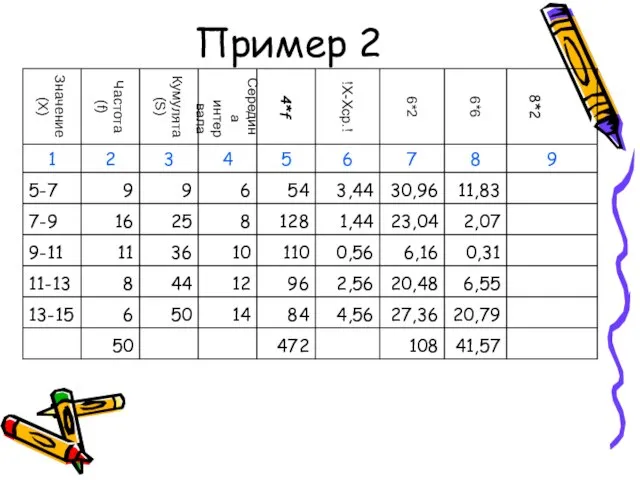
- 49. Пример 2
- 50. Пример 2
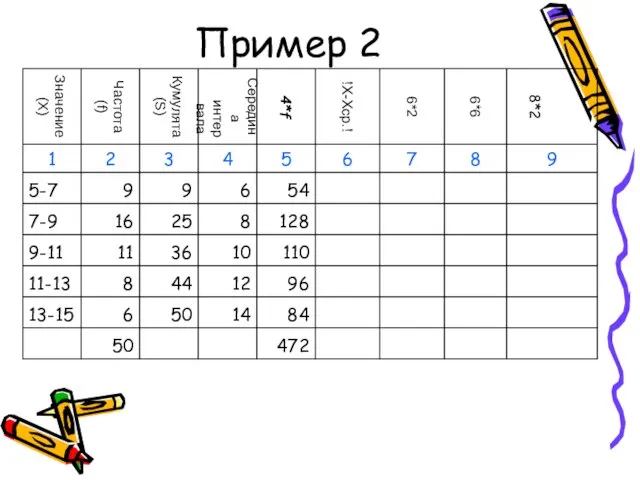
- 51. Пример 2
- 52. Пример 2
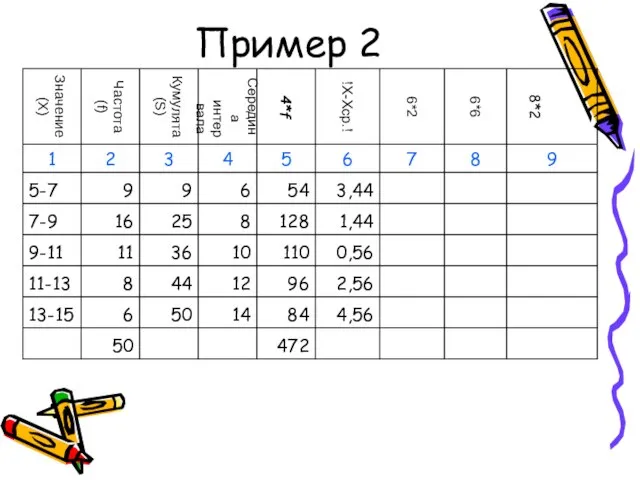
- 53. Пример 2
- 54. Пример 2
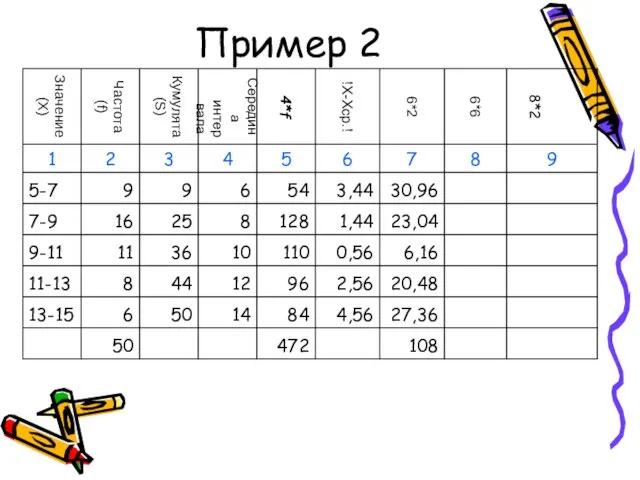
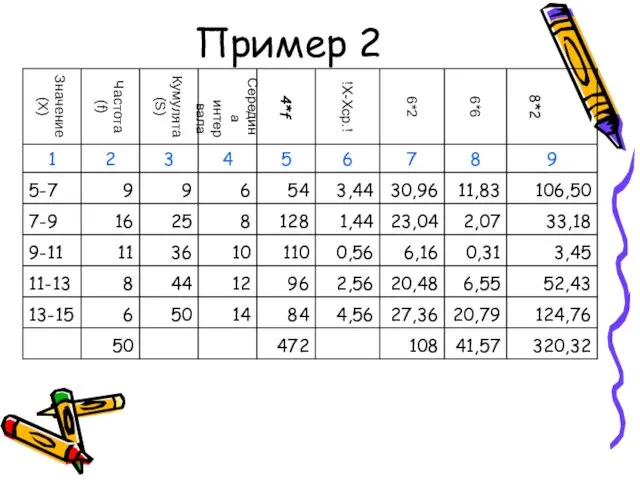
- 55. Пример 2
- 56. Пример 2
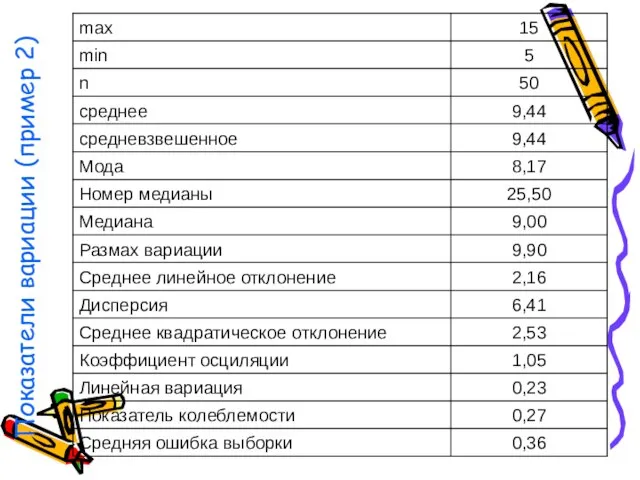
- 57. Показатели вариации (пример 2)
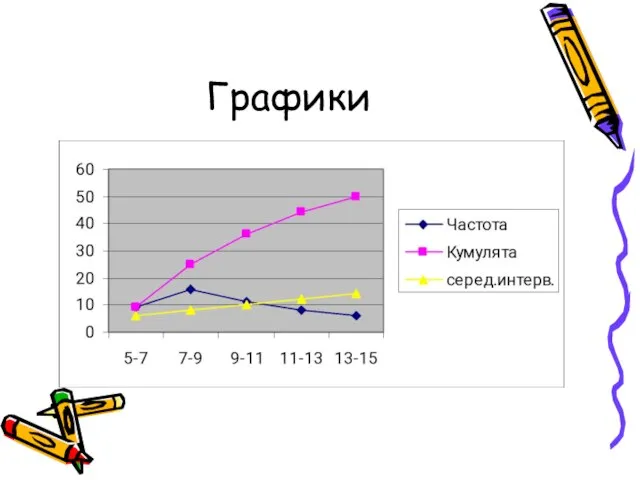
- 58. Графики
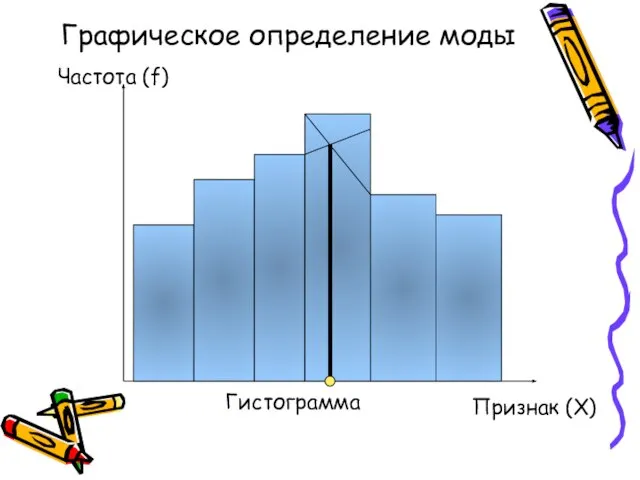
- 59. Графическое определение моды Гистограмма Частота (f) Признак (X)
- 61. Скачать презентацию

























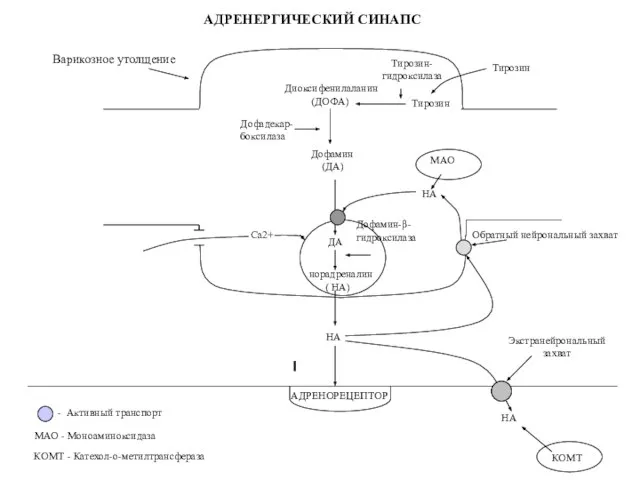 Адреномиметики
Адреномиметики Sport in Canada
Sport in Canada АО Вюрт Северо-Запад, Санкт-Петербург. Боулинг–турнир. Месяц новых клиентов
АО Вюрт Северо-Запад, Санкт-Петербург. Боулинг–турнир. Месяц новых клиентов Презентация на тему Русский герой сказок: Иван-дурак
Презентация на тему Русский герой сказок: Иван-дурак  Путешествие на водопад Атыш
Путешествие на водопад Атыш Помада Creamy Glam
Помада Creamy Glam Презентация по английскому Королевская семья Великобритании
Презентация по английскому Королевская семья Великобритании tema-gribi-rodnaya-tropinka_ru
tema-gribi-rodnaya-tropinka_ru Работа социального педагога с детьми имеющих отклоняющее поведение.
Работа социального педагога с детьми имеющих отклоняющее поведение. Комплекс упражнений утренней гимнастики
Комплекс упражнений утренней гимнастики Службы для электронного общения
Службы для электронного общения Характер и темперамент
Характер и темперамент Обществознание
Обществознание Материально-техническая база одно из условий эффективной реализации профильного обучения.
Материально-техническая база одно из условий эффективной реализации профильного обучения. Способ тепловой обработки сыпучих материалов и устройства для его осуществления
Способ тепловой обработки сыпучих материалов и устройства для его осуществления Архитектура Санкт-Петербурга
Архитектура Санкт-Петербурга project
project Greenway. Жизнь без химии с заботой о семье и природе
Greenway. Жизнь без химии с заботой о семье и природе Адрес: Тверская область, г. Нелидово Ул. Шахтерская 16
Адрес: Тверская область, г. Нелидово Ул. Шахтерская 16 Сказочные птицы
Сказочные птицы Леонардо Да Винчи
Леонардо Да Винчи Как преодолеть стресс перед экзаменом
Как преодолеть стресс перед экзаменом Признаки нарушения адаптации в почерке
Признаки нарушения адаптации в почерке Бонусируемые задачи для ТП, РГТП/МПП, МРТ на июнь 2017
Бонусируемые задачи для ТП, РГТП/МПП, МРТ на июнь 2017 Доходы предприятия и финансовые результаты его деятельности
Доходы предприятия и финансовые результаты его деятельности Алтайский государственный университет
Алтайский государственный университет Методика оформление. Пушкинская карта
Методика оформление. Пушкинская карта Презентация на тему Социальная информатика
Презентация на тему Социальная информатика