Тема урока: Признаки равенства треугольников.

Математический диктант
Вариант 1.
1.Два угла, у которых одна сторона общая,
а две другие являются продолжениями одна другой,
называются…
Вариант 2.
1.Два угла, у которых стороны одного
угла являются продолжениями сторон другого,
называются…

Математический диктант
Вариант 1.
2. Сумма смежных углов равна…
Вариант 2.
2.Свойство вертикальных углов:
вертикальные углы…

Математический диктант
Вариант 1.
3.Треугольник, у которого две стороны равны, называется…
Вариант 2.
3.В равнобедренном треугольнике углы
при основании …

Математический диктант
Вариант 1.
4.В равнобедренном треугольнике биссектриса, проведенная к основанию, является…
Вариант 2.
4.Отрезок, соединяющий вершину
треугольника с серединой противоположной
стороны, называется…

Математический диктант
Вариант 1.
5.Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны,
называется…
Вариант 2.
5. Перпендикуляр, проведенный из вершины
треугольника к прямой, содержащей
противоположную сторону, называется…

Проверка математического диктанта
Вариант 1.
1.Два угла, у которых одна сторона общая, а две другие являются
продолжениями одна другой, называются
смежными.
2. Сумма смежных углов равна
180°.
3.Треугольник, у которого две стороны равны,
называется
равнобедренным.
4.В равнобедренном треугольнике биссектриса, проведенная к
основанию, является
медианой и высотой.
5.Отрезок биссектрисы угла треугольника, соединяющий вершину
треугольника с точкой противоположной стороны,
называется
биссектрисой треугольника.

Проверка математического диктанта
Вариант 2.
1.Два угла, у которых стороны одного
угла являются продолжениями сторон другого,
называются…
2.Свойство вертикальных углов: вертикальные углы…
3.В равнобедренном треугольнике углы при основании …
4.Отрезок, соединяющий вершину
треугольника с серединой противоположной
стороны, называется…
5. Перпендикуляр, проведенный из вершины
треугольника к прямой, содержащей
противоположную сторону, называется…
вертикальными
равны
равны
медианой
высотой

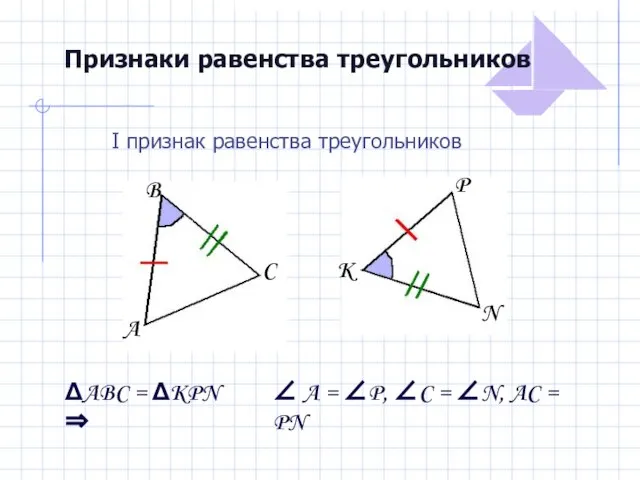
Признаки равенства треугольников
I признак равенства треугольников
ΔABC = ΔKPN ⇒
∠ A = ∠P, ∠C = ∠N, AC = PN
A
B
C
K
P
N

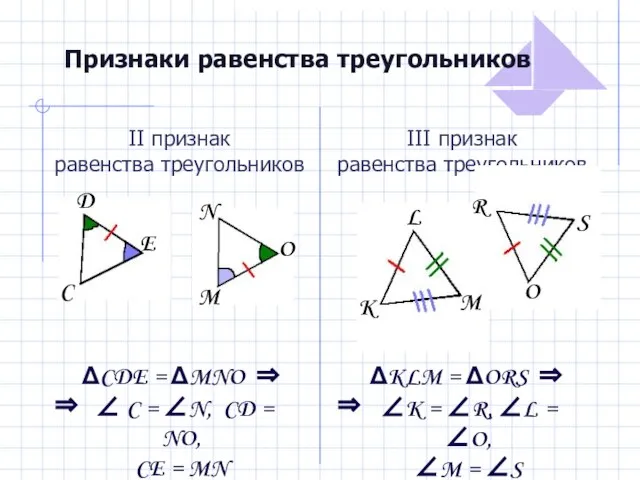
Признаки равенства треугольников
II признак
равенства треугольников
ΔCDE = ΔMNO ⇒
⇒
III признак
равенства треугольников
ΔKLM = ΔORS ⇒
⇒
∠ C = ∠N, CD = NO,
CE = MN
∠K = ∠R, ∠L = ∠O,
∠M = ∠S
C
D
E
M
N
O
K
L
M
S
R
O

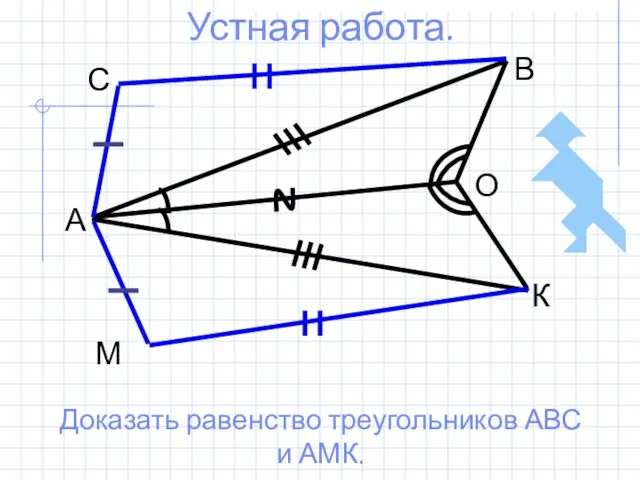
Устная работа.
В
А
С
К
М
Доказать равенство треугольников АВС и АМК.

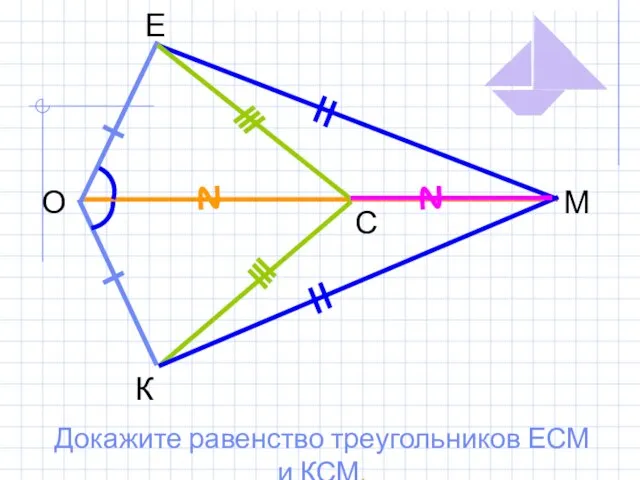
Е
К
О
М
С
Докажите равенство треугольников ЕСМ и КСМ.

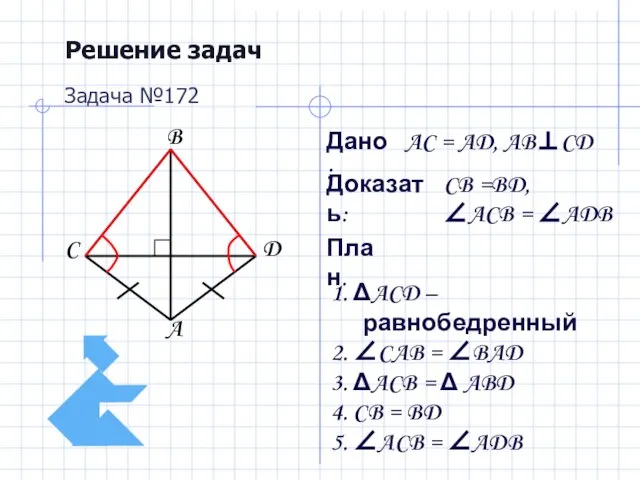
Решение задач
Дано:
Доказать:
План.
Задача №172
AC = AD, AB⊥CD
CB =BD,
∠ACB = ∠ADB
1. ΔACD – равнобедренный
2. ∠CAB = ∠BAD
3. ΔACB = Δ ABD
4. CB = BD
5. ∠ACB = ∠ADB
A
B
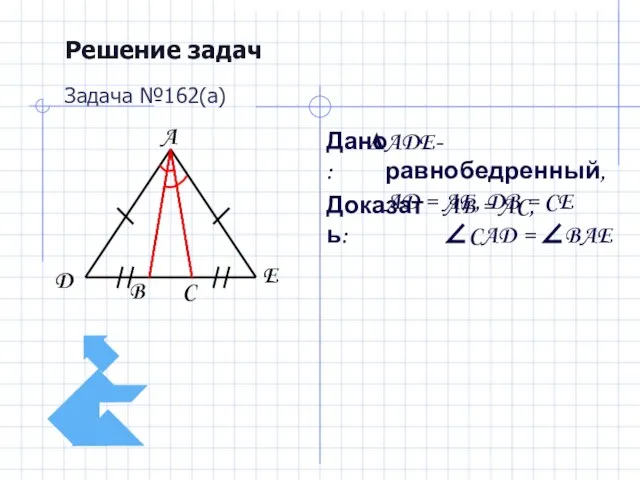
D
C

Решение задач
Дано:
Доказать:
Задача №162(а)
ADE-равнобедренный,
AD = AE, DB = CE
AB = AC,
∠CAD = ∠BAE
A
D
B
C
E

Самостоятельная работа
по рабочей тетради.
Вариант 1
№ 73, 75
Вариант 2
№ 74, 76

Домашнее задание
№ 139, принести циркуль

Спасибо за урок!

Тестовая работа
Алгоритм работы с тестом
1. Внимательно прочитай задачу.
2. Реши задачу.
3. Из четырех предложенных ответов
выбери один правильный.
4. Букву, соответствующую правильному ответу,
занеси в карточку ответов.
5.Приступай к решению следующей задачи.

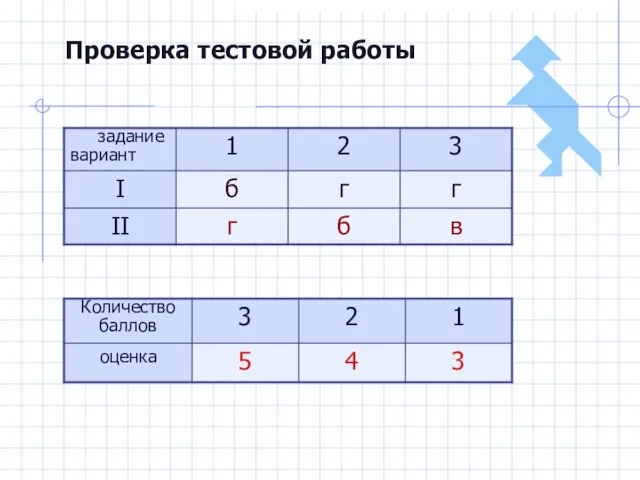
Проверка тестовой работы

Историческая справка
Евклид (конец IV – III в.до н. э.)
Древнегреческий математик;
автор труда «Начала» в 13 книгах,
в котором изложены основы
геометрии, теории чисел, метод
определения площадей и объемов;
оказал огромное влияние на
развитие математики.