Степень числа с натуральным показателем

Просмотрите слайды и вы будете:
Знать:
Определение степени;
Свойства степени с натуральным показателем;
Определение одночлена;
Стандартный вид одночлена.
Уметь:
Умножать степени;
Возводить в степень;
Делить степени;
Упрощать выражения, содержащие степень;
Умножать одночлены;
Возводить одночлены в степень.

Определение
Степенью числа ак, где к -натуральное число, а- любое, называется произведение к множителей, каждый из которых равен а:

называют:
а - основанием степени;
к– показателем степени;
а к – степенью.

например: произведение равных множителей можно записать так:
а·а·а·а·а·а·а=а7;
(а - в) ·(а - в) ·(а - в)=(а - в)3;
(-3х) ·(-3х) ·(-3х) ·(-3х) ·(-3х) =(-3 х)5;
(5у)·(5у) ·(6а) ·(6а) ·(6а)=(5у)2·(6а)3.

Свойства степени

Умножение степеней:
При умножении степени на степень с одинаковым основанием показатели складывают.

Например
а5а3=а8;
х7х4=х11;
хххх4=х7;
(-х)(-х)3=(-х)4.

Проверь себя!

Вычисли 23 это
6
8

Подумай

Правильно

Деление степеней
При деление степеней с одинаковым основание показатели вычитают.

Например
х8:х3=х5;
у6:у=у5;
а10:а2=а8;
в5:в5=в0=1.

Проверь себя!

Вычисли 36:33 это
32
33

Подумай

Молодец

Возведение степени в степень
При возведение степени в степень нужно перемножить показатели

Например
(х2)3=х6;
(у4)2=у8;
(а5)0=а0=1.

Вычисли

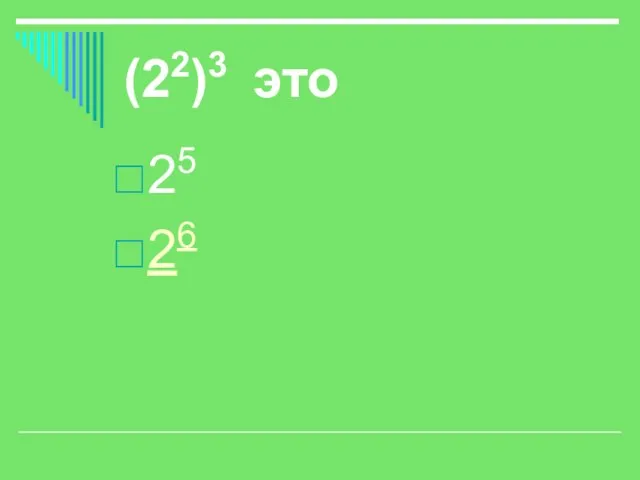
(22)3 это
25
26

Подумай

Молодец

Степень произведения
При возведении произведения в степень возводится в степень каждый из множителей

Например
(5ав)4=54а4в4=625а4в4;
(-2а2в)2=(-2)2а4в2=4а4в2;

одночлены

Определение одночлена
Выражение, представляющее собой произведение чисел, переменных и степеней переменных, называется одночленом.

например
Выражения 3ах4, -2в4,45а6в2 – одночлены.
Выражения а - в, (а-2с),а2+в7 - не являются одночленами.

Стандартный вид одночлена
Стандартным видом одночлена называется произведение, составленное из числового множителя (коэффициента) и буквенного выражения, в котором каждая из переменных взята в натуральной степени.

Например
-8а3в2, 6ах5 одночлены стандартного вида
-2ххх4, 34а3аахх-одночлены не стандартного вида

Степень одночлена
Степенью одночлена стандартного вида называется сумма показателей степеней переменных

например
8х4у2 – одночлен шестой степени.
Степень одночлена 3х равна единице.
Степень одночлена 5 равна нулю.

Приведение подобных слагаемых
Одночлены, отличающиеся только числовым коэффициентом или равные между собой называются подобными.

Например
3х-5х+24х= 22х;
2ав+7ав -8ав = 1ав=ав;
5х+18х – 12у+9у =23х – 3у;
2х2-5х2+9х2=6х2;
4ав3+6ав3=10ав3.