Суперкомпьютер и дискретная топология.(кодирование комплексов)

Великолепная семерка.
В.А.Мельников в кругу выдающихся математиков.
Сидят: С.М.Никольский, Л.С.Понтрягин, А.Н.Тихонов, Г.И.Марчук. Стоят: Ю.В.Прохоров, В.А.Мельников, С.П.Новиков.

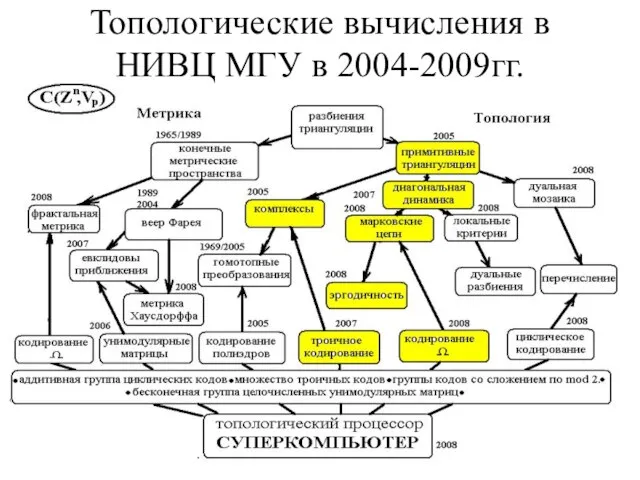
Топологические вычисления в НИВЦ МГУ в 2004-2009гг.

База топологических построений
Rn- n-мерное евклидово пространство.
Zn- подпространство целых точек Rn , как множество вершин объектов.
Vp –множество простых (примитивных) ребер, не имеющих внутренних целых точек, р-максимальный модуль |Δхi | (i=1-n);
{Zn,Vp}-база.

k-грани n-куба.
Грани n-куба :
Вершины-грани 0-размерности,
Ребра-грани 1-размерности,
Грани 2-размерности.(квадраты)
k-грани n-куба- грани размерностей 0≤k≤n.
n-грань в n-кубе- сам n-куб.
Грани в n-кубе – кубы меньших размерностей.

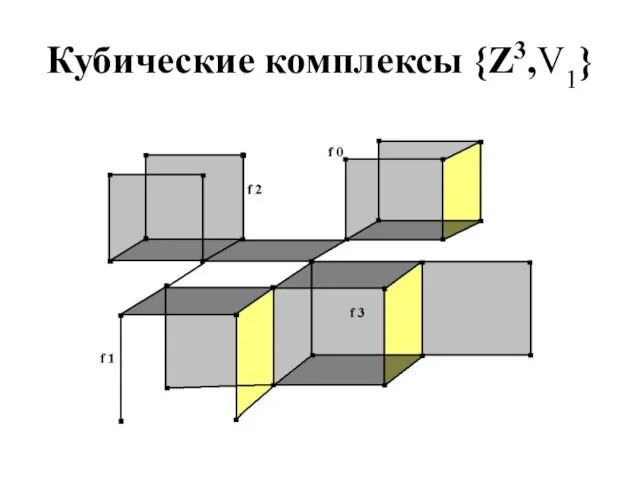
Кубические комплексы {Z3,V1}

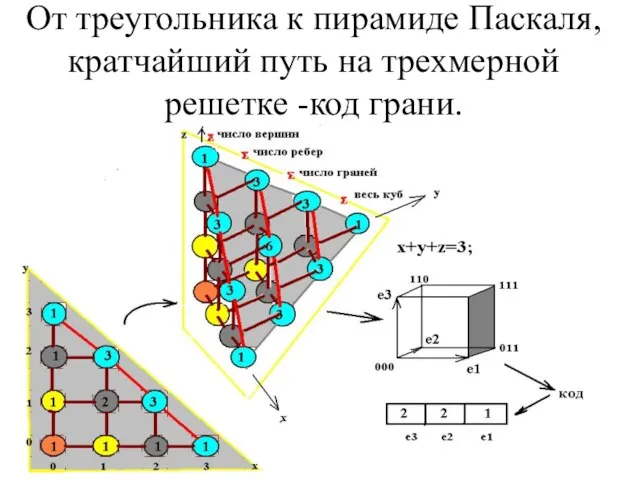
От треугольника к пирамиде Паскаля, кратчайший путь на трехмерной решетке -код грани.

Кодирование k-граней n-куба.
D=d1 d2 …dn; n-разрядное слово
e1 e2… en;
dim=2;m=1-k; ?ei1 x ei2 x…eik;
djr=0,1;r=1-(n-k);?T{0,1};
D?Пei+T{0,1};
220121-3-грань (e1xe2xe5) в 6-кубе (220020)транс.из (000000)?(000101)

Биекция {In}?{3n}.
к-грань в n-кубе = троичный n-разрядный код с k двойками в разрядах, чьи номера равны номерам задействованных реперных векторов.
Для 3-куба:
000,001,010,…111 -вершины;
002,012,020,021,102,112,…211-ребра;
022,122,202,212,220,221 -грани;
222 -3-куб;

Кодирование комплексов.
Алфавит {0;1;2}
Слово из n букв - грань в n-кубе;
Строка из m слов – кубический комплекс в In
Строки с n-координатами-комплекс в Rn.
Определение пересечений и поглощений комплексов? поразрядные операции.
202121,021122, 022201,221101-комплекс размерности 3 в 6-мерном пространстве, связный, общая вершина 001101.
К=Q/2 (размерность)+Т/1(трансляция).

Операции пересечения и поглощения
Ø-пустое множество
0-отсутствие трансляции
1- наличие трансляции
2-наличие ребра

Бутылка Клейна в R3 (Z3,V1).

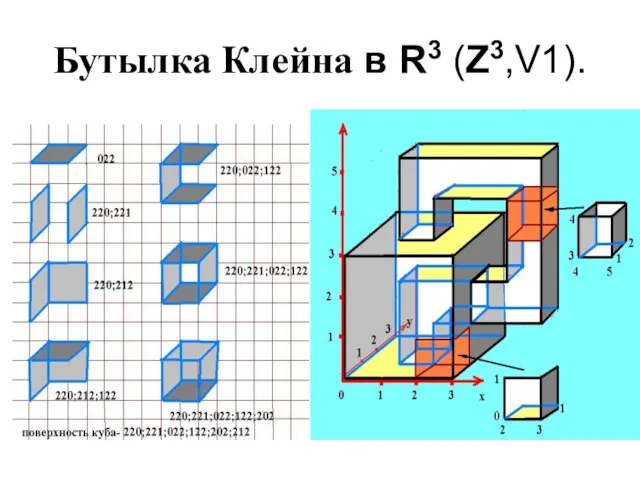
Бутылка в памяти.
Трехмерный байтовый массив.
В байте-номер комплекса (в данном случае двумерного)
Бутылка Клейна- «емкостью» 75 байт.
«Панельное» топологическое строительство.

Кодирование - конструктивный подход к перечислению Ω
Случайная динамика перестроек комплексов- цепь Маркова.
Корректное (аксиоматика Колмогорова) вычисление переходных вероятностей – через перечисление Ω в кодовом представлении.
Анализ эргодических и периодических свойств цепей Маркова-поведение степеней матриц переходных вероятностей.

Динамика примитивных триангуляций R3. Кодирование диагоналей в гранях плоских разверток куба.
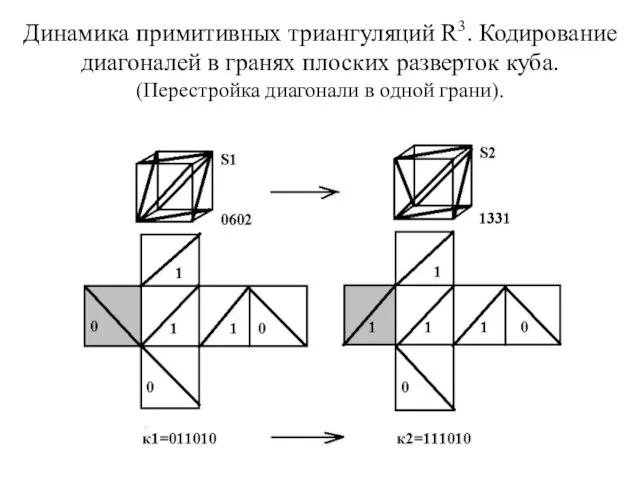
(Перестройка диагонали в одной грани).

Спектр вершинных полиэдров в примитивно триангулированном R3.(суперкомпьютер МГУ «Чебышев»)

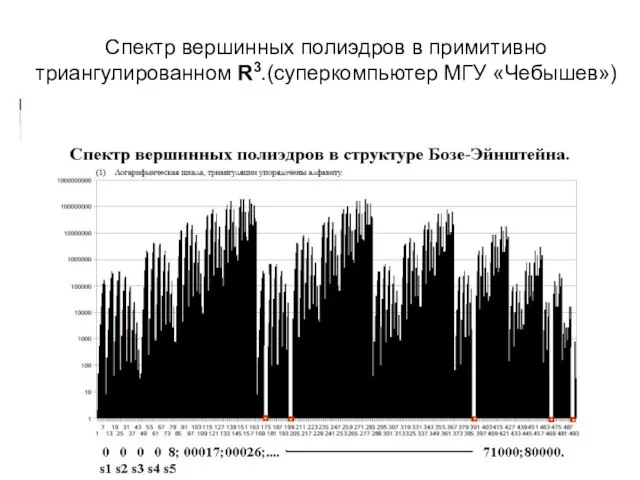
Перспективы т-кодирования.
Представление «полуквантовыми» т-кодами n-мерных комплексов (c их симметриями) и их проекций в меньшие размерности.
Распараллеливание вычислений до поразрядных операций.
Действие cимметрической группы Sn на комплекс, как на строку слов.
Учет т-кодовых представлений и операций над ними в архитектуре будущих суперкомпьютеров.