Содержание
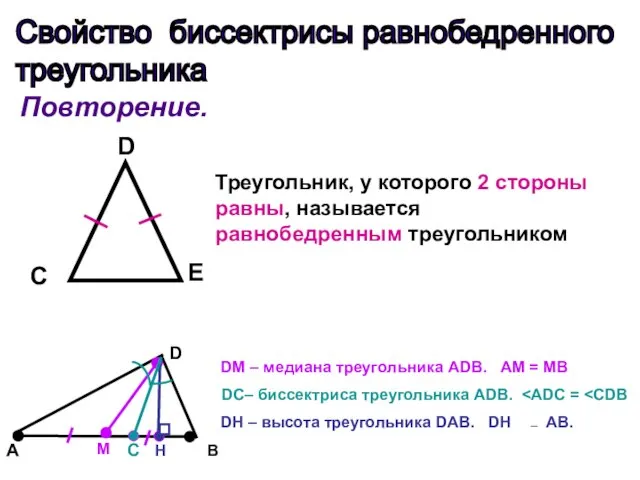
- 2. Свойство биссектрисы равнобедренного треугольника Повторение. Треугольник, у которого 2 стороны равны, называется равнобедренным треугольником D С
- 3. Теорема: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой. A С B Дано:
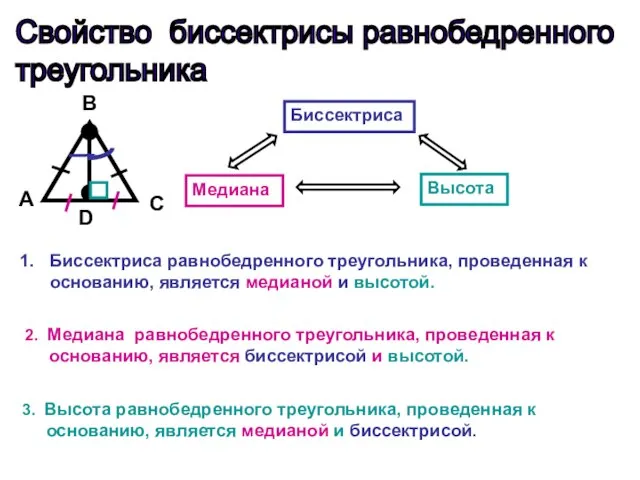
- 4. Свойство биссектрисы равнобедренного треугольника A С D B Биссектриса Медиана Высота Биссектриса равнобедренного треугольника, проведенная к
- 6. Скачать презентацию

 Постмодернизм
Постмодернизм Расчёт себестоимости 15 блинов из кукурузной муки
Расчёт себестоимости 15 блинов из кукурузной муки Презентация на тему Русская культура второй половины XIX века
Презентация на тему Русская культура второй половины XIX века  6 класс«Волна»
6 класс«Волна» 10 занимательных фактов из истории Олимпийских игр
10 занимательных фактов из истории Олимпийских игр Перенос слов.
Перенос слов. Мифологизация Использование мифа для формирования имиджа Выполнила: Шадрина Маргарита, 401 группа Проверила: Быстрова Татьяна Юр
Мифологизация Использование мифа для формирования имиджа Выполнила: Шадрина Маргарита, 401 группа Проверила: Быстрова Татьяна Юр Слуховой анализатор. Орган равновесия
Слуховой анализатор. Орган равновесия Презентация на тему Урок математики в 1 классе
Презентация на тему Урок математики в 1 классе Тиристоры. Лекция 5
Тиристоры. Лекция 5 Занятия аппликацией как средство развития творчества детей
Занятия аппликацией как средство развития творчества детей Лайфхаки по написанию курсовой работы и научной статьи
Лайфхаки по написанию курсовой работы и научной статьи Nox Bot. Автоматизация торговли на Forex
Nox Bot. Автоматизация торговли на Forex Представление о мультимедийных продуктах
Представление о мультимедийных продуктах Социальный проект как программа реальных действий
Социальный проект как программа реальных действий Общественно-политическое развитие России в 1894 – 1904 гг.
Общественно-политическое развитие России в 1894 – 1904 гг. 2011 год
2011 год План маркетинга. Цена
План маркетинга. Цена Создание презентации в Microsoft Power Point
Создание презентации в Microsoft Power Point Нежилое помещение. Фото (3)
Нежилое помещение. Фото (3) Государственное образовательное учреждение «Школа-интернат № 15 циркового профиля для детей-сирот и детей, оставшихся без попече
Государственное образовательное учреждение «Школа-интернат № 15 циркового профиля для детей-сирот и детей, оставшихся без попече Пионеры-герои (7 класс)
Пионеры-герои (7 класс)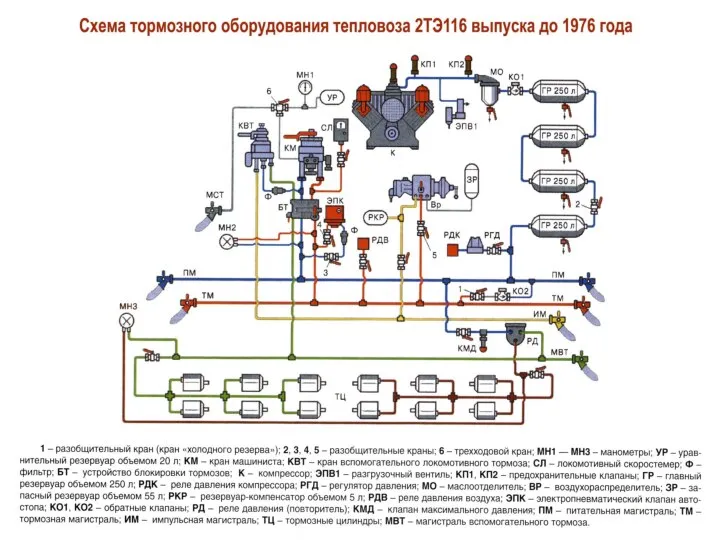 Схема тормозного оборудования тепловоза 2ТЭ116 выпуска до 1976 года
Схема тормозного оборудования тепловоза 2ТЭ116 выпуска до 1976 года Место и роль закона в системе общего права
Место и роль закона в системе общего права Применение современных технологий в пищевой промышленности
Применение современных технологий в пищевой промышленности Бисер, вышивка бисером
Бисер, вышивка бисером Работа школьного музея2009-2010 учебный год
Работа школьного музея2009-2010 учебный год Полюби себя
Полюби себя