Содержание
- 2. Ко́нус — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через
- 3. Определения. Конусом (точнее, круговым конусом) называется тело, которое состоит из круга — основания конуса, точки, не
- 4. Виды конусов. Если основание конуса имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция
- 5. Виды конусов.
- 6. Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания. Телесный угол при
- 7. Теорема 1. Площадь боковой и полной поверхности конуса с радиусом R и образующей L выражаются формулами:
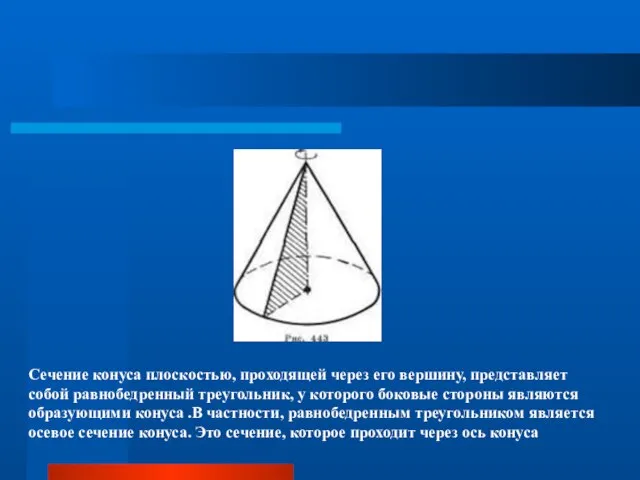
- 8. Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются
- 9. Теорема 3. Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность - по
- 14. Скачать презентацию
Слайд 2Ко́нус — тело, полученное объединением всех лучей, исходящих из одной точки (вершины
Ко́нус — тело, полученное объединением всех лучей, исходящих из одной точки (вершины

Объединение образующих конуса называется образующей (или боковой) поверхностью конуса. Образующая поверхность конуса является конической поверхностью.
Понятие.
Слайд 3Определения.
Конусом (точнее, круговым конусом) называется тело, которое состоит из круга — основания
Определения.
Конусом (точнее, круговым конусом) называется тело, которое состоит из круга — основания

Слайд 4Виды конусов.
Если основание конуса имеет центр симметрии (например, является кругом или эллипсом)
Виды конусов.
Если основание конуса имеет центр симметрии (например, является кругом или эллипсом)

Косой (наклонный) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
Круговой конус — конус, основание которого является кругом.
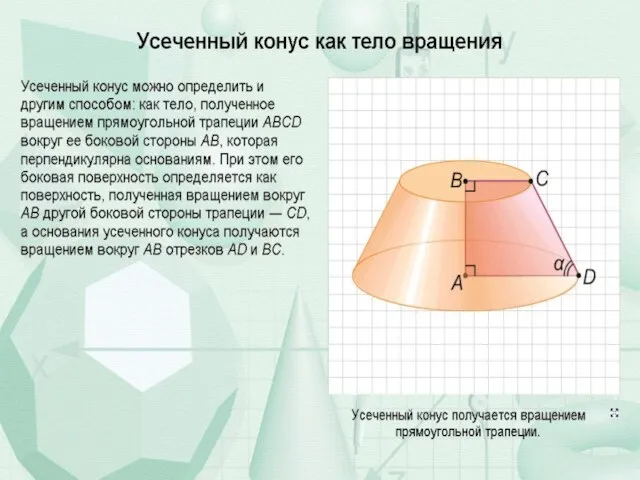
Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса).
Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный объём).
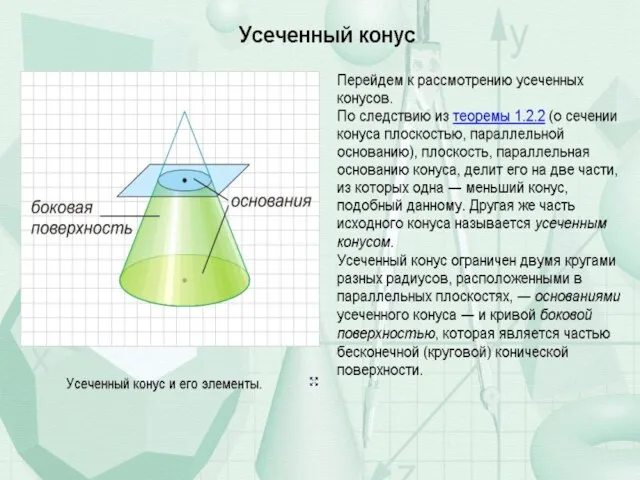
Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом. Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания. Таким образом, все конусы, опирающиеся на данное основание и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.
Слайд 5Виды конусов.
Виды конусов.

Слайд 6Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от
Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от

Телесный угол при вершине прямого кругового конуса равен
— угол раствора конуса (то есть удвоенный угол между осью конуса и любой прямой на его боковой поверхности).
Слайд 7Теорема 1.
Площадь боковой и полной поверхности конуса с радиусом R и образующей
Теорема 1.
Площадь боковой и полной поверхности конуса с радиусом R и образующей

Объем кругового конуса равен
Пересечение плоскости с прямым круговым конусом является одним из конических сечений (в невырожденных случаях — эллипсом, параболой или гиперболой, в зависимости от положения секущей плоскости). В алгебраической геометрии конус — это произвольное подмножество K векторного пространства V над полем F, для которого для любого
λK = K
Теорема 2.
Слайд 8Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у
Слайд 9Теорема 3.
Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую
Теорема 3.
Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую

Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса и перпендикулярная плоскости осевого сечения, содержащей эту образующую
Теорема 4.

 Таджикистан
Таджикистан Калистеника - комплекс упражнений с весом собственного тела
Калистеника - комплекс упражнений с весом собственного тела Слова-запреты и общепринятые речевые штампы, отрицательно влияющие на профессионального оператора колл-центра
Слова-запреты и общепринятые речевые штампы, отрицательно влияющие на профессионального оператора колл-центра Защита гражданских прав
Защита гражданских прав Ты знаешь единицы измерения?
Ты знаешь единицы измерения? Легкая атлетика. Футбол. Гимнастика
Легкая атлетика. Футбол. Гимнастика Значение термина искусство. Проблемы определения
Значение термина искусство. Проблемы определения Притча о маме
Притча о маме Наша помощница - швейная иголочка
Наша помощница - швейная иголочка Презентация на тему Вводные слова и обращения
Презентация на тему Вводные слова и обращения Законы газового состояния вещества
Законы газового состояния вещества Функция y=cos(x)
Функция y=cos(x) Умножение и деление многозначных чисел
Умножение и деление многозначных чисел В процессе исторического развития живые организмы освоили четыре среды обитания.
В процессе исторического развития живые организмы освоили четыре среды обитания. Unit 3
Unit 3 СИСТЕМА ГЕОДЕЗИЧЕСКОГО ОБЕСПЕЧЕНИЯ НА ОСНОВЕ ПРИМЕНЕНИЯ СИСТЕМ GPS И ГЛОНАСС.
СИСТЕМА ГЕОДЕЗИЧЕСКОГО ОБЕСПЕЧЕНИЯ НА ОСНОВЕ ПРИМЕНЕНИЯ СИСТЕМ GPS И ГЛОНАСС. Food and drink
Food and drink Комплексный учебный курс"Основы религиозных культур и светской этики» :
Комплексный учебный курс"Основы религиозных культур и светской этики» : Физическое воспитание учащихся средствами игровой направленности в рамках внедрения ФГОС
Физическое воспитание учащихся средствами игровой направленности в рамках внедрения ФГОС Weather and climate of Belarus
Weather and climate of Belarus Портфолио – модель индивидуального образовательного маршрута
Портфолио – модель индивидуального образовательного маршрута Head [hed] голова
Head [hed] голова Презентация на тему Скажи "Нет"!
Презентация на тему Скажи "Нет"!  Presentation_3 (1)
Presentation_3 (1) Путешествие на планету положительных и отрицательных чисел
Путешествие на планету положительных и отрицательных чисел Нормативно-правовое обеспечение молодых специалистов и работников, обучающихся без отрыва от производства на предприятии
Нормативно-правовое обеспечение молодых специалистов и работников, обучающихся без отрыва от производства на предприятии Сравнение динамики продаж в экспериментальных и контрольных точках
Сравнение динамики продаж в экспериментальных и контрольных точках Трансфертное ценообразование В данном документе представлен краткий обзор основных положений закона о трансфертном ценообраз
Трансфертное ценообразование В данном документе представлен краткий обзор основных положений закона о трансфертном ценообраз