Свойство _____________равнобедренного треугольника.

Повторение
Ребус
Доказательство теоремы
Задача на применение теоремы
Содержание

Для доказательства теоремы нам нужно повторить некоторые понятия:
Признаки равенства треугольников
Свойство смежных углов
Что такое биссектриса
Что такое высота
Что такое медиана
Приступим!
Повторение

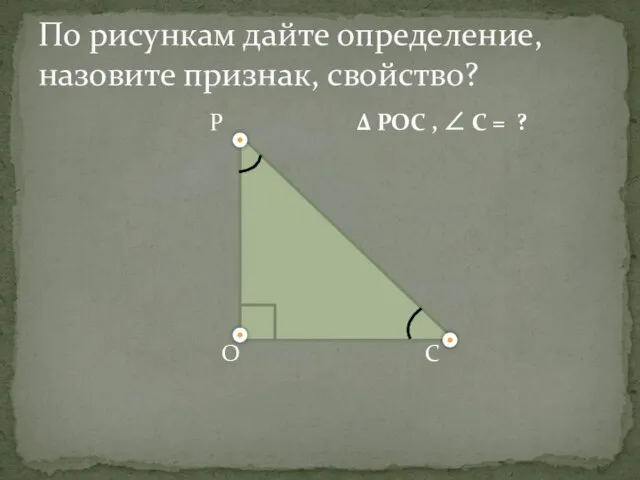
P Δ POC , ∠ С = ?
O C
По рисункам дайте определение, назовите признак, свойство?

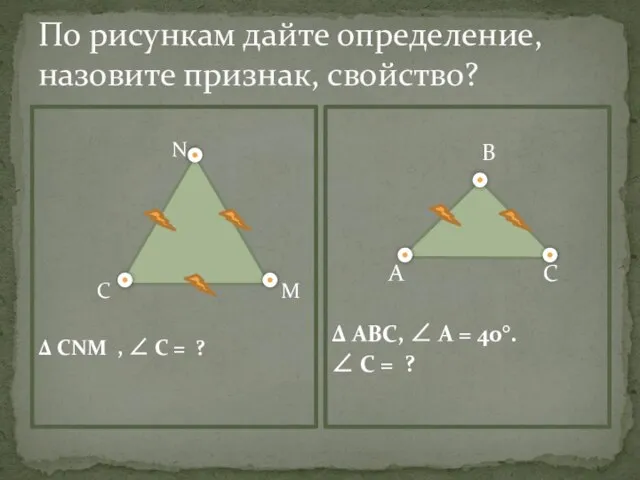
По рисункам дайте определение, назовите признак, свойство?
N
С M
Δ СNM , ∠ С = ?
В
А С
Δ АВС, ∠ А = 40°.
∠ С = ?

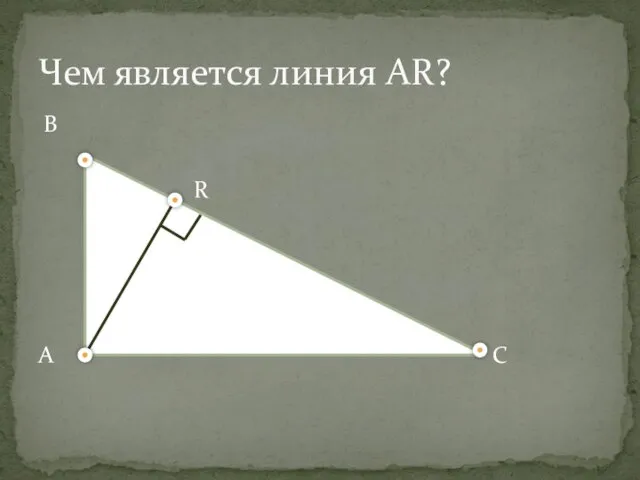
Чем является линия AR?
B
R
A С

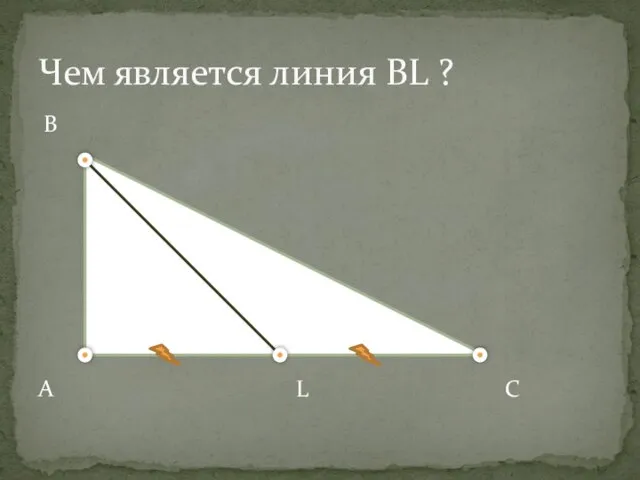
Чем является линия BL ?
B
A L С

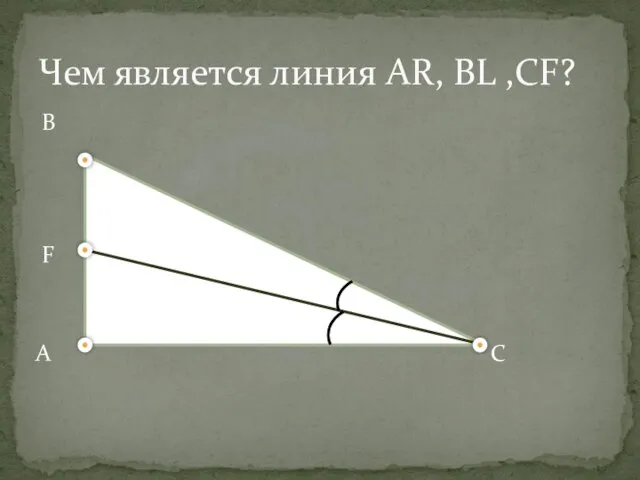
Чем является линия AR, BL ,CF?
B
F
A С

∠ (ab) = ∠ (bc)
a
b c
Какое свойство изображено на рисунке?

А К
L O
Какой из признаков изображен на рисунке?
A D
P
N M

,
РЕБУС.
3
а

МЕЧ ДИВАН А
МЕДИАНА
ПРАВИЛЬНО

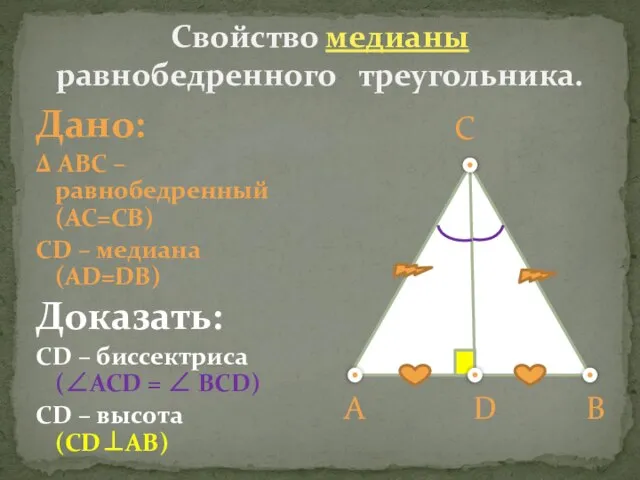
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Свойство медианы
равнобедренного треугольника

Дано:
Δ АВС – равнобедренный (АС=СВ)
СD – медиана (AD=DB)
Доказать:
CD – биссектриса (∠ACD = ∠ BCD)
CD – высота (CD⊥AB)
Свойство медианы
равнобедренного треугольника.

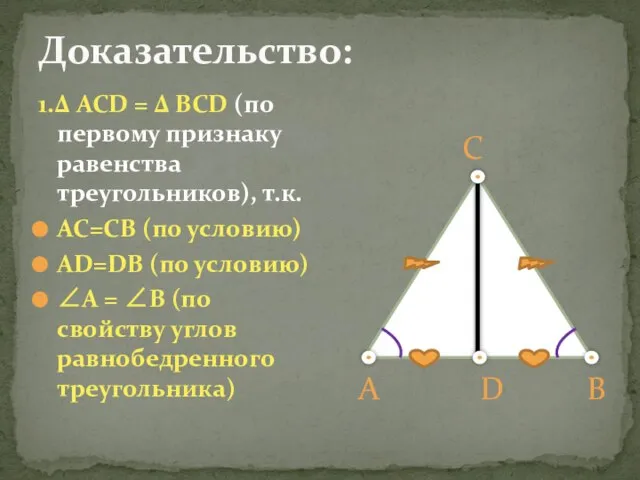
1.Δ ACD = Δ BCD (по первому признаку равенства треугольников), т.к.
AC=CB (по условию)
AD=DB (по условию)
∠A = ∠B (по свойству углов равнобедренного треугольника)
Доказательство:

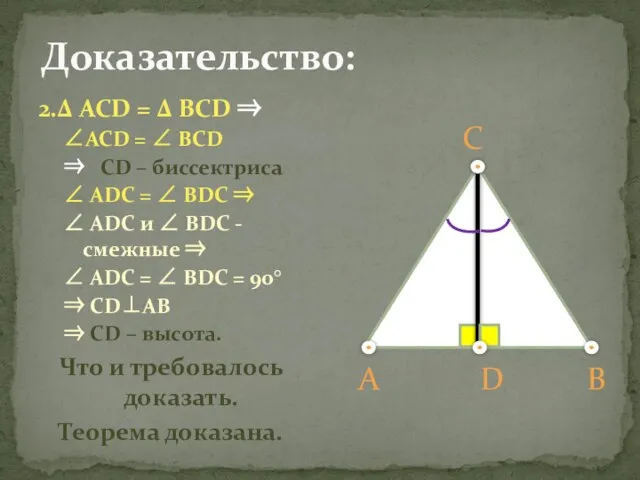
2.Δ ACD = Δ BCD ⇒
∠ACD = ∠ BCD
⇒ CD – биссектриса
∠ ADC = ∠ BDC ⇒
∠ ADC и ∠ BDC - смежные ⇒
∠ ADC = ∠ BDC = 90°
⇒ CD⊥AB
⇒ CD – высота.
Что и требовалось доказать.
Теорема доказана.
Доказательство:
С
D
В
А

Поэтому справедливы также следующие утверждения:
Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
Таким образом, установлено, что биссектриса, медиана и высота равнобедренного треугольника, проведенные к основанию, совпадают.

Дано:
Δ АВС -равнобедренный
ВN – медиана,
∠ABN = 35°
Найти:
∠NBC = ?
∠BАC = ?
Задача.
В
N
С
А