Схеми на свързване на ОУ с ООВ

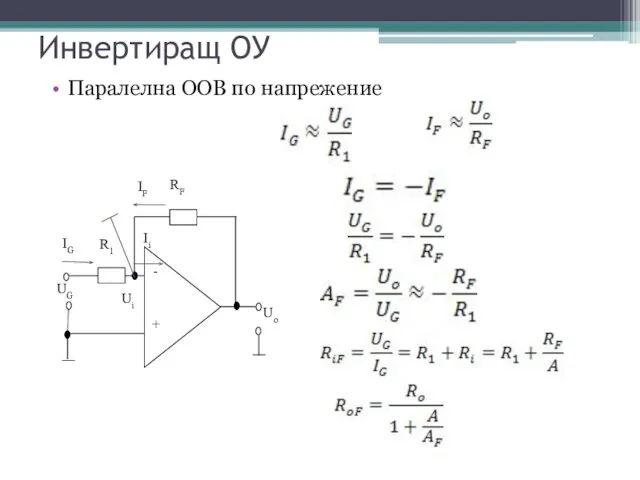
Инвертиращ ОУ
Паралелна ООВ по напрежение

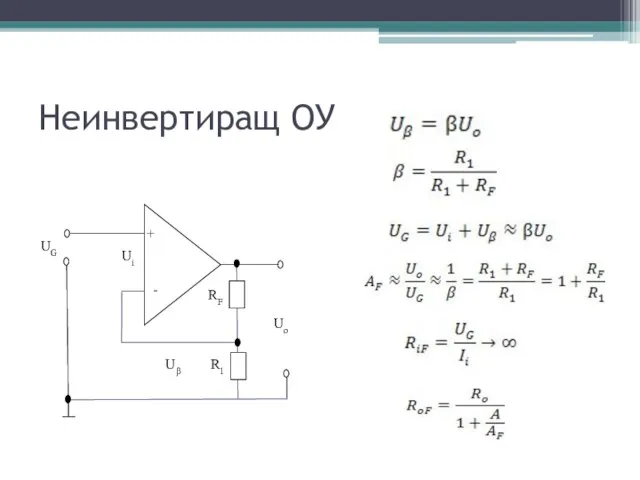
Неинвертиращ ОУ

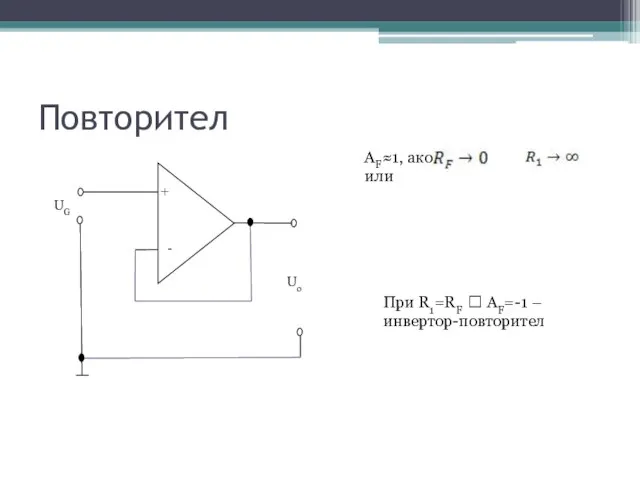
Повторител
AF≈1, ако или
При R1=RF ? AF=-1 –
инвертор-повторител

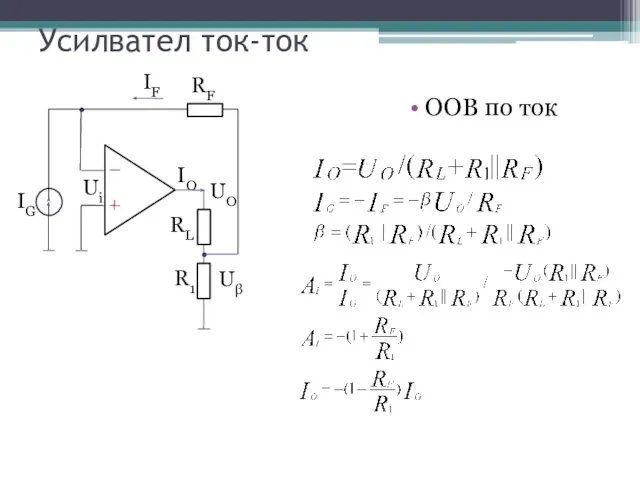
Усилвател ток-ток
ООВ по ток
IG
Ui
IF
RF
RL
R1
IO
UO
Uβ

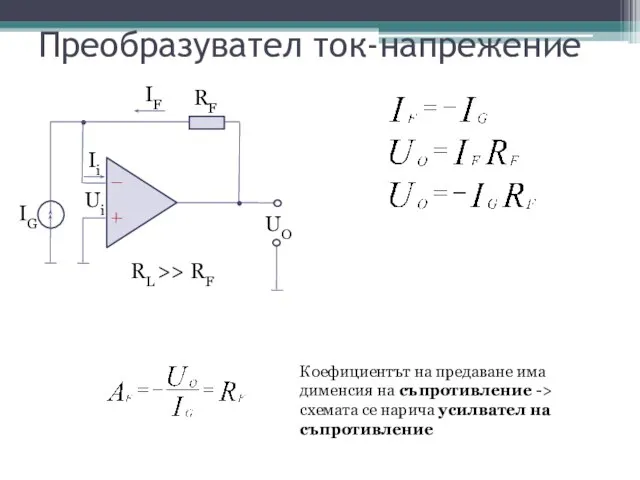
Преобразувател ток-напрежение
Коефициентът на предаване има дименсия на съпротивление -> схемата се нарича усилвател на съпротивление

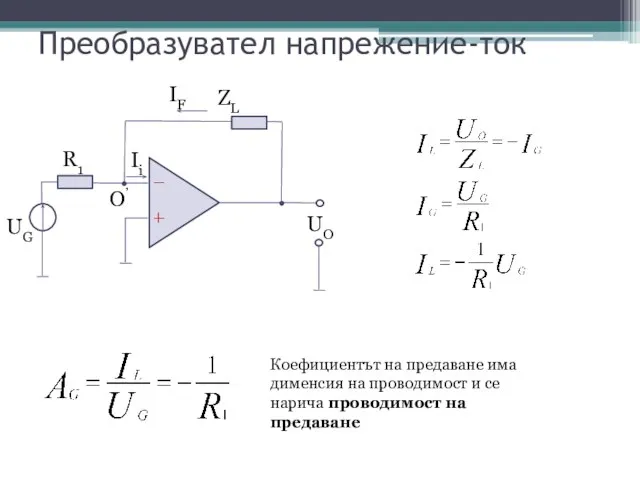
Преобразувател напрежение-ток
Коефициентът на предаване има дименсия на проводимост и се нарича проводимост на предаване

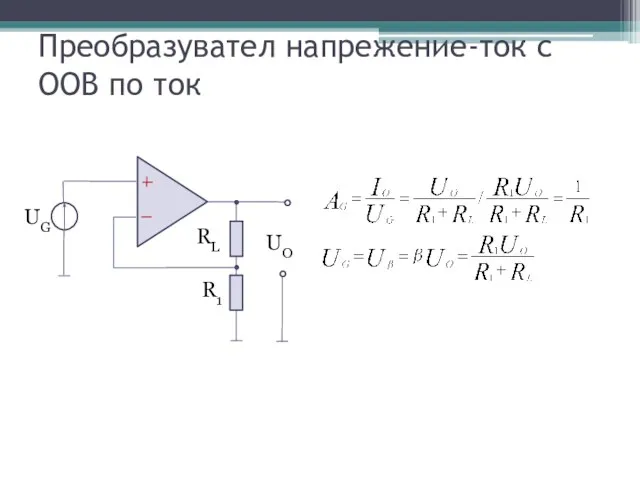
Преобразувател напрежение-ток с ООВ по ток

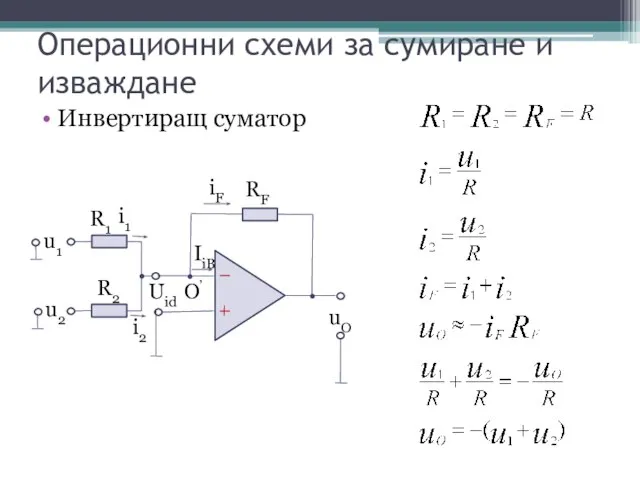
Операционни схеми за сумиране и изваждане
Инвертиращ суматор

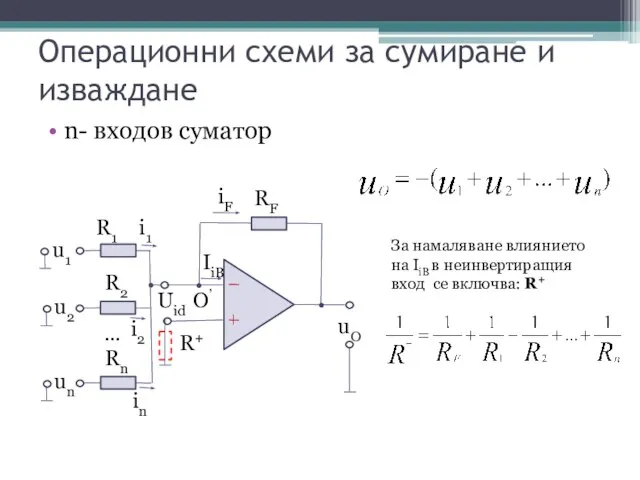
Операционни схеми за сумиране и изваждане
n- входов суматор
За намаляване влиянието на IiB в неинвертиращия вход се включва: R+

Операционни схеми за сумиране и изваждане
Суматор с мащабни коефициенти – ако
R1≠ R2 ≠ RF, то схемата на суматора може да се използва за решаване на уравния от вида:
- при n на брой входове

Пример
Да се реши уравнението: y=2x1+5x2
Избира се RF=100K
От RF/R1=2 и RF/R2=5 се намира:
R1= RF/2=50K, R2=RF/5=20K
RF/R1 и RF/R2 се наричат мащабни коефициенти

Операционни схеми за сумиране и изваждане
Схема за намиране средната стойност от n входа
Приема се, че R1= R2=…= Rn и RF/ R1=1/n
Тогава:

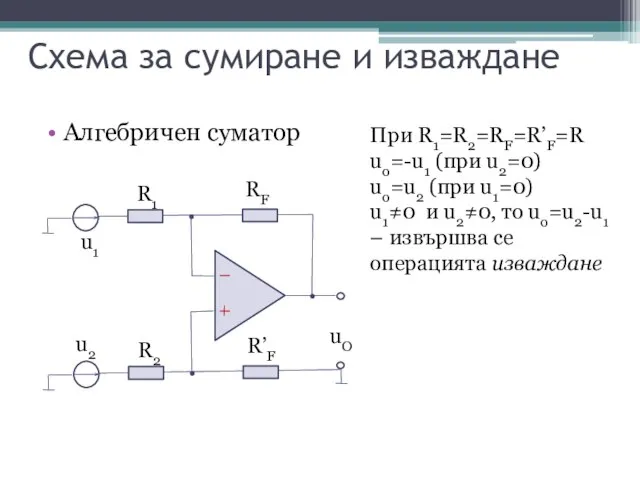
Схема за сумиране и изваждане
Алгебричен суматор
При R1=R2=RF=R’F=R
uo=-u1 (при u2=0)
uo=u2 (при u1=0)
u1≠0 и u2≠0, то uo=u2-u1 – извършва се операцията изваждане

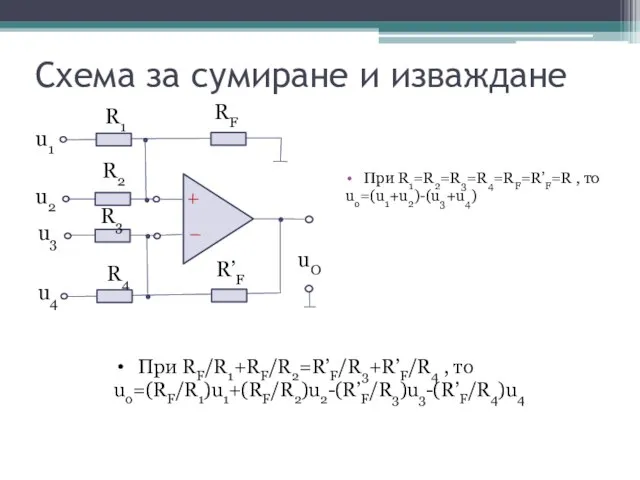
Схема за сумиране и изваждане
При R1=R2=R3=R4=RF=R’F=R , то
uo=(u1+u2)-(u3+u4)
При RF/R1+RF/R2=R’F/R3+R’F/R4 , то
uo=(RF/R1)u1+(RF/R2)u2-(R’F/R3)u3-(R’F/R4)u4

Пример
Да се моделира зависимостта:
uo=u1+2u2-0,5u3
При RF=R’F=100K

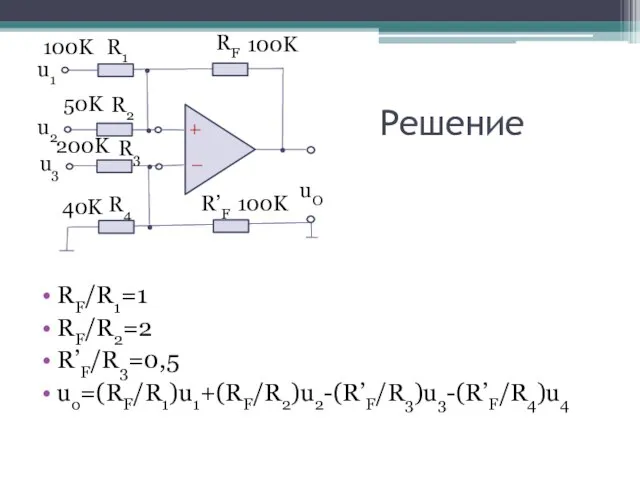
Решение
RF/R1=1
RF/R2=2
R’F/R3=0,5
uo=(RF/R1)u1+(RF/R2)u2-(R’F/R3)u3-(R’F/R4)u4

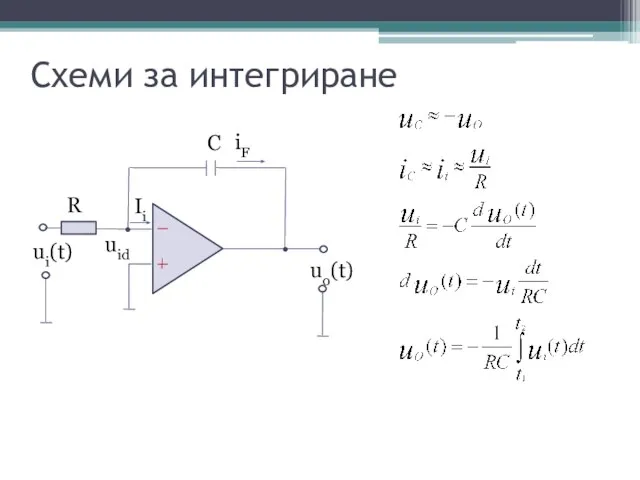
Схеми за интегриране

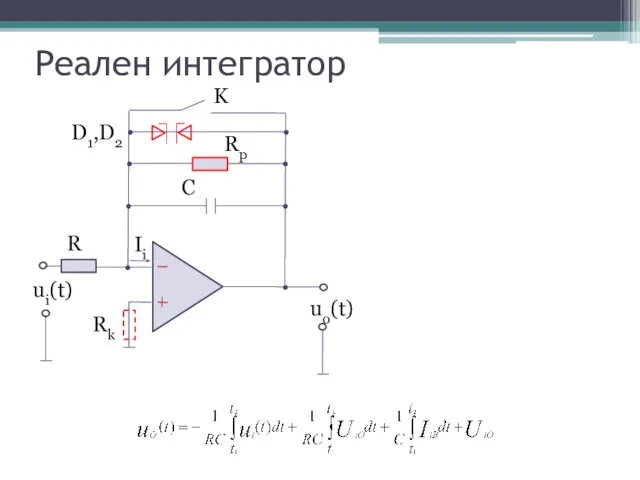
Реален интегратор

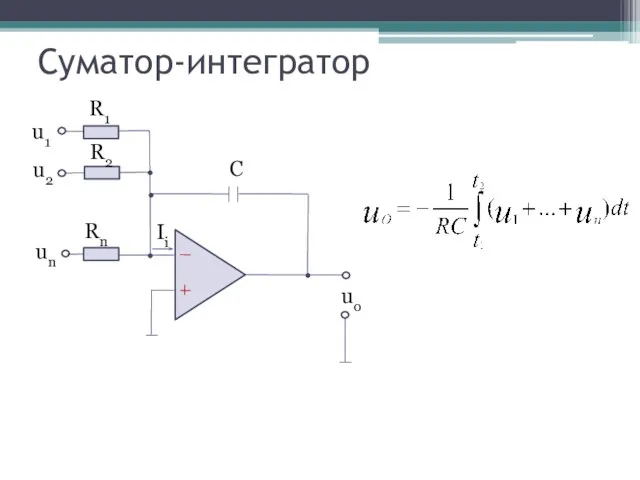
Суматор-интегратор

Схеми за диференциране

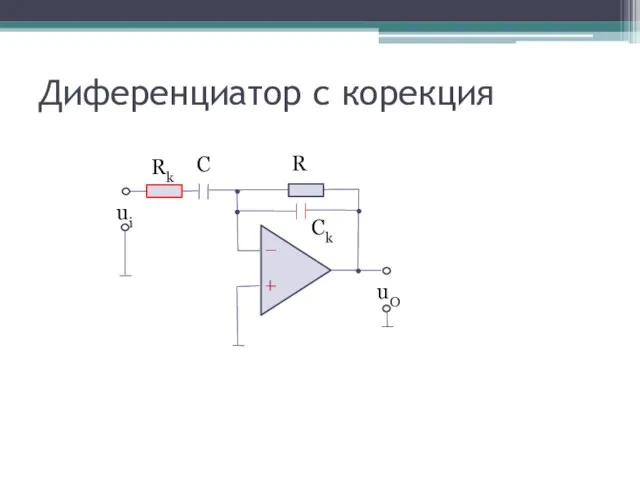
Диференциатор с корекция