ТЕЛА ВРАЩЕНИЯ: КОНУС ЦИЛИНДР

К О Н У С

Площадь поверхности конуса

Сечения конуса
Сечение плоскостью, параллельной оси
Сечение плоскостью, параллельной основанию
Сечение – круг с центром в т. О1

УСЕЧЕННЫЙ КОНУС

ЦИЛИНДР

За площадь боковой поверхности цилиндра принимают площадь её развертки
Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра.
Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований.
П Л О Щ А Д Ь П О В Е Р Х Н О С Т И Ц И Л И Н Д Р А
Sбок=2πrh
Sцил=2 πr(r+h)

С Е Ч Е Н И Я Ц И Л И Н Д Р А
Сечение плоскостью, перпендикулярной к оси,
в сечении круг.

ПРИМЕРЫ ЗАДАЧ С РЕШЕНИЯМИ ПО ТЕМЕ
«СЕЧЕНИЕ КОНУСА И ЦИЛИНДРА»
Задача 1.
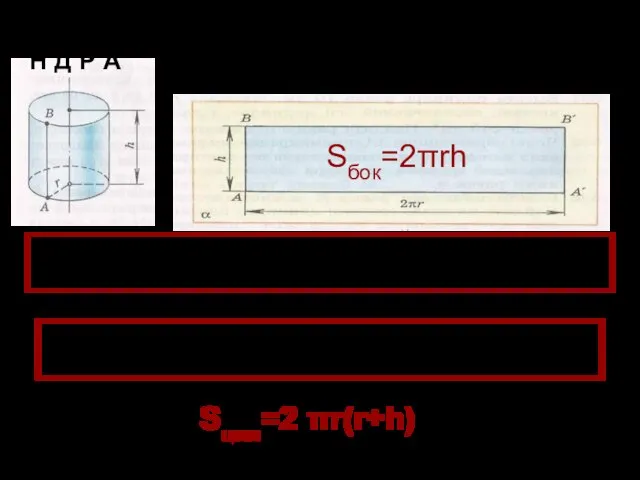
Высота цилиндра равна 12см, а радиус основания равен 10 см. Цилиндр пересечён плоскостью, параллельной оси, так, что в сечении получился квадрат. Найти расстояние от оси цилиндра до секущей плоскости.
Решение:
По условию задачи r=10, а h=12.
Для нахождения расстояния от оси до плоскости сечения нужно найти величину расстояния ОН. Отрезок ОН перпендикулярен к стороне квадрата АВ, которая равна12см. ОА и ОВ равны радиусу основания r=10см. ΔОАВ равнобедренный, ОН делит сторону АВ пополам. Таким образом, задача сводится к нахождению катета в прямоугольном треугольнике ОНА, который будет равен, по теореме Пифагора, квадратному корню из (102 - 62)=8.
Задача 2.
Площадь осевого сечения конуса равна 0,6 см2. Высота конуса равна 1,2 см. Вычислите площадь полной поверхности конуса.
Решение:
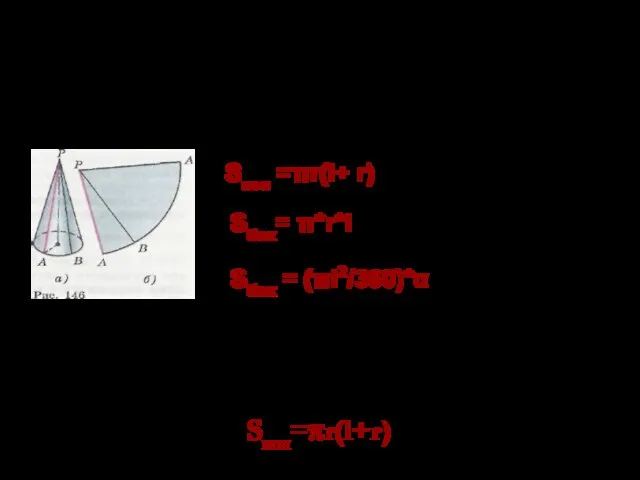
Формула нахождения площади полной поверхности конуса равна Sкон=πr(l+r) (1). В осевом сечении конуса получается треугольник, у которого основание равно 2r, высота h=1,2см и площадь S=0,6 см2. Из формулы площади треугольника S=1/2*2r*h (2r-основание треугольника) находим r=0,5. Зная катет треугольника АВО, равный r, и гипотенузу, равную h, можем найти второй катет, равный l. По теореме Пифагора он равен корню квадратному из (1,22+0,52)=1,3. Теперь, зная все составляющие величины формулы (1), подставив, получаем
S= π*05*(1,3+0,5)=0,9 π.