Содержание
- 2. Проблемная ситуация Эксперты утверждают, что 29% всех преступлений совершаются несовершеннолетними. Чтобы проверить это утверждение, мы взяли
- 3. Еще одна проблемная ситуация В прошлом году компания АВС провела исследование и выяснила, что 5% покупателей
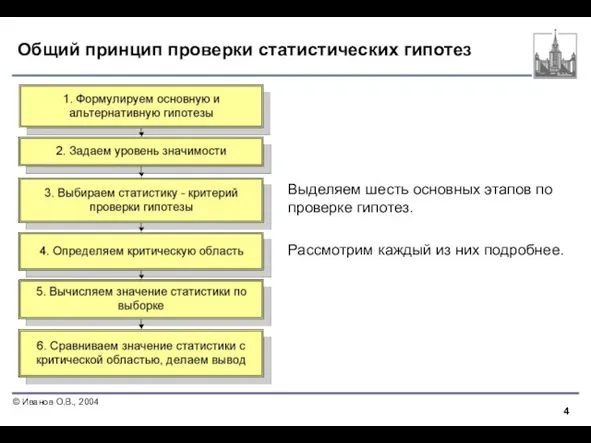
- 4. Общий принцип проверки статистических гипотез Выделяем шесть основных этапов по проверке гипотез. Рассмотрим каждый из них
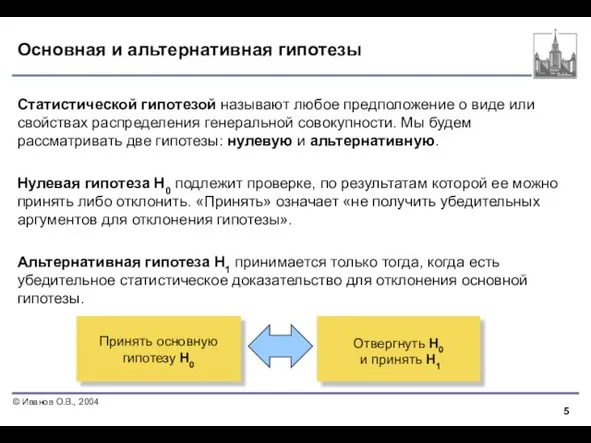
- 5. Основная и альтернативная гипотезы Статистической гипотезой называют любое предположение о виде или свойствах распределения генеральной совокупности.
- 6. Примеры основной и альтернативной гипотезы Основные гипотезы: Альтернативные гипотезы:
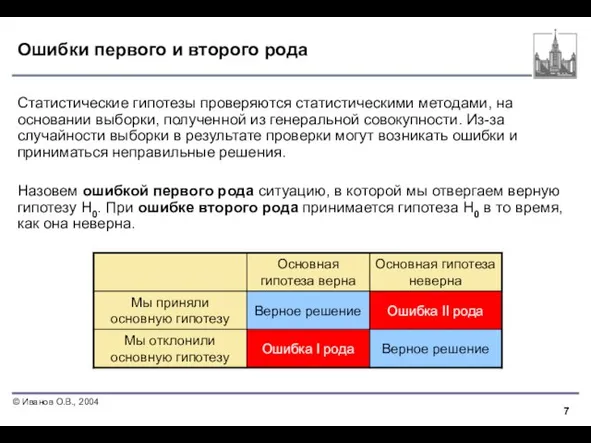
- 7. Ошибки первого и второго рода Статистические гипотезы проверяются статистическими методами, на основании выборки, полученной из генеральной
- 8. Уровень значимости гипотезы Уровнем значимости гипотезы назовем допустимую вероятность совершить ошибку первого рода, то есть принять
- 9. Статистика - критерий проверки гипотезы Каким образом на основании выборки принимается решение? Для этого необходима специальная
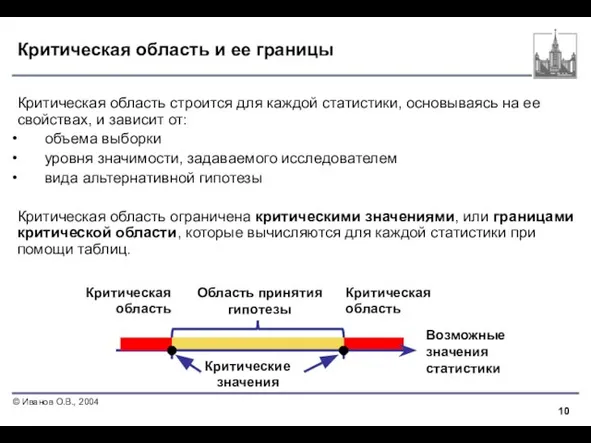
- 10. Критическая область и ее границы Критическая область строится для каждой статистики, основываясь на ее свойствах, и
- 11. Получение вывода После построения критической области вычисляется значение статистики по выборке. Затем сравнивается полученное значение статистики
- 12. 9.2. Гипотеза о среднем Гипотеза Статистика Алгоритм Пример
- 13. Гипотезы Требуется проверить предположение о значении среднего для нормально распределенной генеральной совокупности. Нулевая и альтернативная гипотезы
- 14. Статистика (σ известно) В качестве статистики выбираем следующую случайную функцию: где - выборочное среднее - гипотетическое
- 15. Распределение статистики Формула для статистики представляет собой следующее выражение: Используемая статистика имеет нормальное распределение. При проверке
- 16. Распределение статистики Используемая статистика имеет нормальное распределение. При проверке гипотезы пользуемся известными нам свойствами нормального распределения.
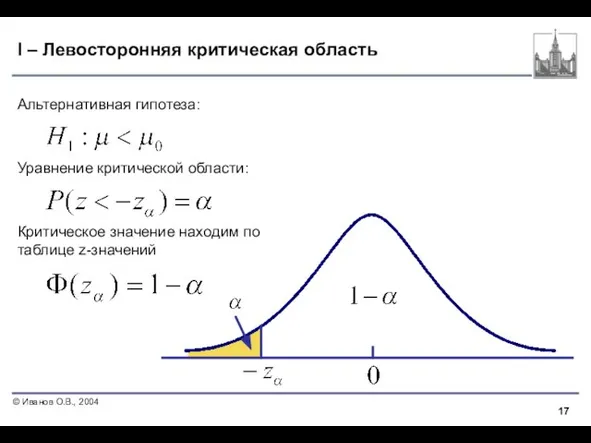
- 17. I – Левосторонняя критическая область Альтернативная гипотеза: Уравнение критической области: Критическое значение находим по таблице z-значений
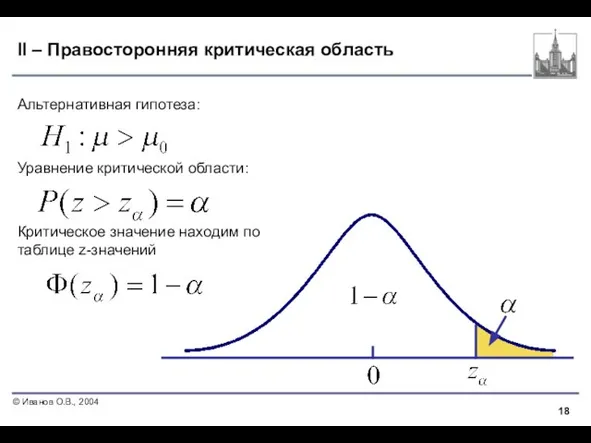
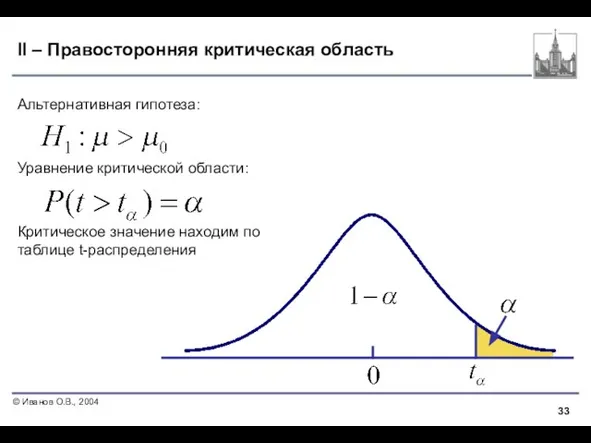
- 18. II – Правосторонняя критическая область Альтернативная гипотеза: Уравнение критической области: Критическое значение находим по таблице z-значений
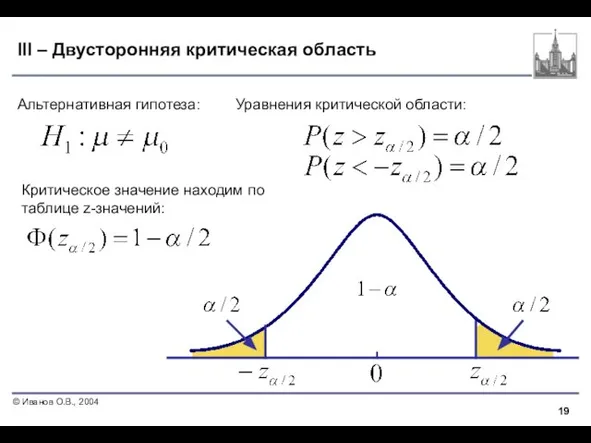
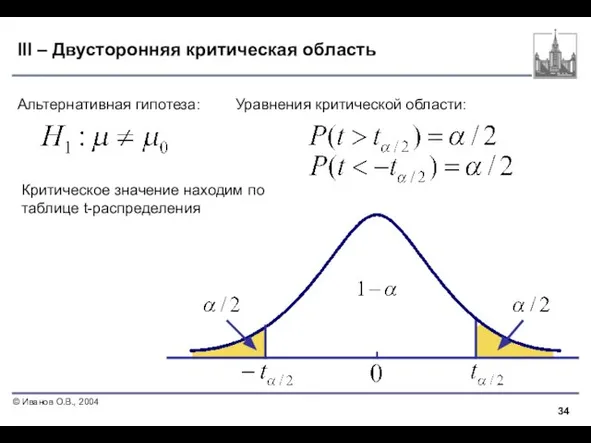
- 19. III – Двусторонняя критическая область Альтернативная гипотеза: Уравнения критической области: Критическое значение находим по таблице z-значений:
- 20. Получение выводов Построив критическую область, вычислим значение статистики по выборке. Для получения выводов мы должны проверить,
- 21. Последовательность действий Шаг 1. Сформулировать основную и альтернативную гипотезы. Шаг 2. Задать уровень значимости α. Шаг
- 22. Пример. Детали двигателя Для производства двигателей требуются детали диаметром 70 мм. Поставщик гарантирует: μ=70 мм при
- 23. Пример. Балтика-6 Мы хотим проверить, что содержание алкоголя в сорте 6 пива «Балтика» в соответствует указанному
- 24. Пример. Такие разные преподаватели Преподаватель N. немецкого языка хочет протестировать новый метод заучивания новых слов. По
- 25. Задача. Булочки для котлет Фабрика по производству полуфабрикатов закупает булочки на хлебозаводе, чтобы использовать их при
- 26. Решение Шаг 1. Основная и альтернативная гипотезы: Н0 : μ ≥ 45 Н1: μ Шаг 2.
- 27. Решение Шаг 5. Сравним полученное значение с критической областью. Полученное значение статистики попало в критическую область.
- 28. Если σ неизвестно … Предыдущая проверка гипотезы о среднем проводилась при условии, что нам известно стандартное
- 29. Гипотезы – те же самые Требуется проверить предположение о значении среднего для нормально распределенной генеральной совокупности.
- 30. Статистика В качестве статистики выбираем следующую случайную функцию: где - выборочное среднее - гипотетическое генеральное среднее
- 31. Распределение статистики Используемая статистика имеет t-распределение c количеством степеней свободы df = n - 1. Для
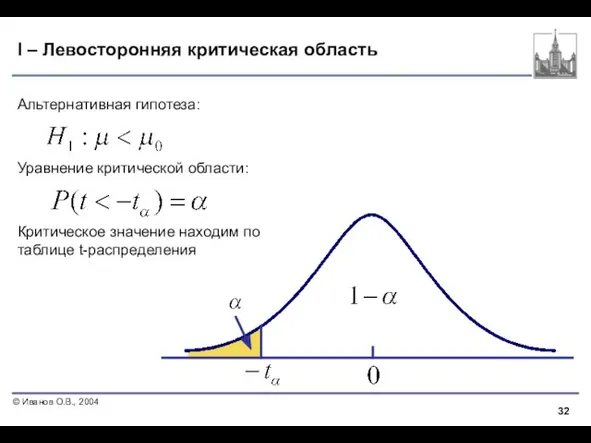
- 32. I – Левосторонняя критическая область Альтернативная гипотеза: Уравнение критической области: Критическое значение находим по таблице t-распределения
- 33. II – Правосторонняя критическая область Альтернативная гипотеза: Уравнение критической области: Критическое значение находим по таблице t-распределения
- 34. III – Двусторонняя критическая область Альтернативная гипотеза: Уравнения критической области: Критическое значение находим по таблице t-распределения
- 35. Получение выводов Построив критическую область, вычислим значение статистики по выборке. Для получения выводов мы должны проверить,
- 36. Пример На семинарах.
- 37. 9.3. Гипотеза о доли Гипотеза о среднем Алгоритм Пример
- 38. Гипотезы Требуется проверить предположение о значении доли генеральной совокупности. Нулевая и альтернативная гипотезы могут быть трех
- 39. Статистика В качестве статистики выбираем следующую случайную функцию: где - выборочная доля - гипотетическая доля генеральной
- 40. Распределение статистики Используемая статистика имеет нормальное распределение. При проверке гипотезы пользуемся известными нам свойствами нормального распределения.
- 41. Получение выводов Построив критическую область, вычислим значение статистики по выборке. Для получения выводов мы должны проверить,
- 42. Пример. Брак лампочек При поставке 10 тыс. лампочек доля брака не должна превышать 0,02. Покупателю будет
- 43. Пример. Новый продукт Компания год назад провела исследование и выяснила, что 5% покупателей заинтересованы в выпуске
- 44. Решение Шаг 1. Основная и альтернативная гипотезы: Шаг 2. Задан уровень значимости α=0,05. Шаг 3. По
- 45. Решение Шаг 5. Сравним полученное значение с критической областью. Полученное значение статистики попало в критическую область.
- 46. 9.4. Гипотеза о дисперсии Постановка проблемы Гипотеза о среднем Алгоритм Пример
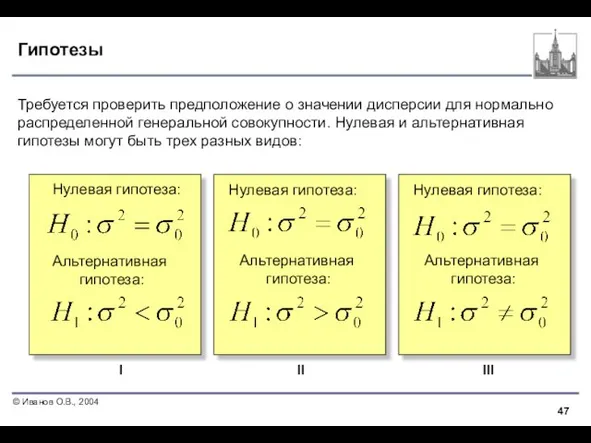
- 47. Гипотезы Требуется проверить предположение о значении дисперсии для нормально распределенной генеральной совокупности. Нулевая и альтернативная гипотезы
- 48. Статистика В качестве статистики выбираем следующую случайную функцию: где - гипотетическая дисперсия генеральной совокупности - стандартное
- 49. Распределение статистики Используемая статистика имеет χ2-распределение c числом степеней свободы df = n - 1. Для
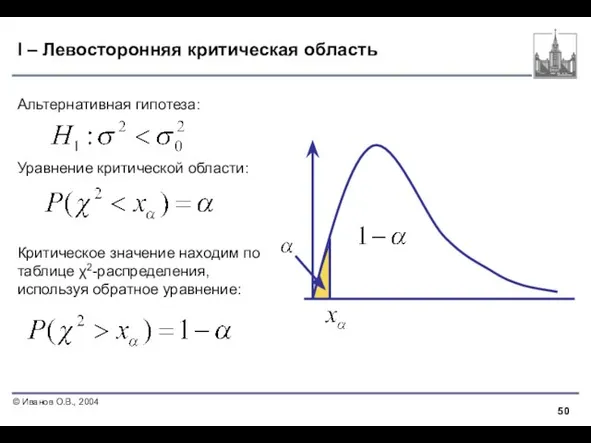
- 50. I – Левосторонняя критическая область Альтернативная гипотеза: Уравнение критической области: Критическое значение находим по таблице χ2-распределения,
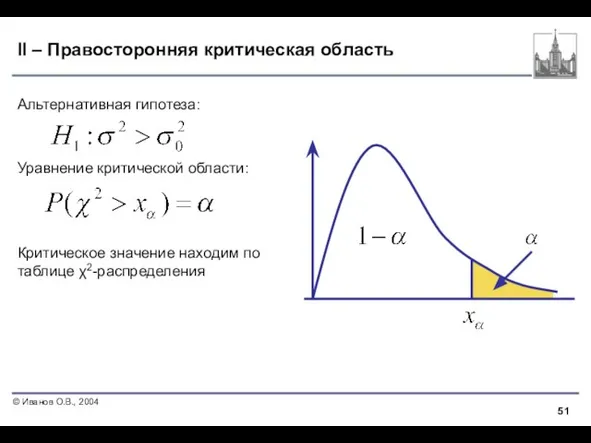
- 51. II – Правосторонняя критическая область Альтернативная гипотеза: Уравнение критической области: Критическое значение находим по таблице χ2-распределения
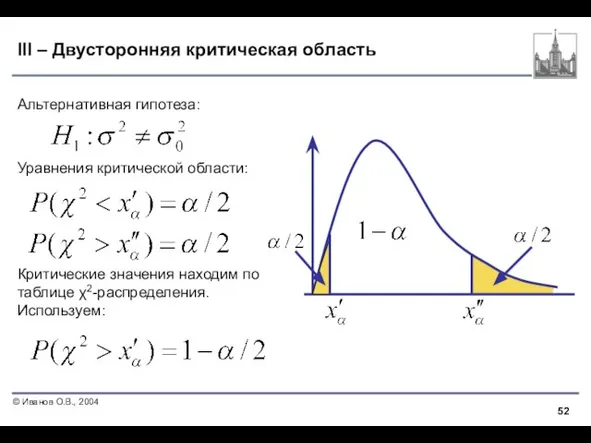
- 52. III – Двусторонняя критическая область Альтернативная гипотеза: Уравнения критической области: Критические значения находим по таблице χ2-распределения.
- 53. Получение выводов Построив критическую область, вычислим значение статистики по выборке. Для получения выводов мы должны проверить,
- 54. Пример. На семинаре.
- 55. Задание на 5 минут Ответьте своими словами, зачем, по вашему мнению, строят доверительные интервалы.
- 56. Задачи 9.1. Эксперты утверждают, что 29% всех ограблений совершаются людьми, не достигшими 18-ти лет. Проверьте это
- 57. Задачи 9.4. Менеджер банка утверждает, что размер ссуды, выдаваемой клиентам банка, составляет в среднем 4800$. Стандартное
- 58. Задачи 9.6. Водитель утверждает, что ГИБДД города выписывает в среднем 60 штрафов за превышение скорости в
- 59. Задачи 9.8. Основываясь на своем прошлом опыте, преподаватель полагает, что средний балл за экзамен равен 75.
- 60. Задачи 9.10. Крупная больница ввела программу физической подготовки, чтобы уменьшить количество пропусков работы по причине болезни.
- 62. Скачать презентацию












































 Политический режим. Демократия
Политический режим. Демократия Презентация по истории на тему: "Смута" в России в конце XVI – начале XVII вв.: Причины. Основные этапы и итоги.
Презентация по истории на тему: "Смута" в России в конце XVI – начале XVII вв.: Причины. Основные этапы и итоги. Родительское собрание -тренинг
Родительское собрание -тренинг инструменты в гараже
инструменты в гараже Портфоліо бібліотекаря абонементу бібліотеки ім. М. Горького
Портфоліо бібліотекаря абонементу бібліотеки ім. М. Горького Презентация на тему История утюга
Презентация на тему История утюга  Планирование. Как проехать в Пейдж
Планирование. Как проехать в Пейдж Колдовские числа
Колдовские числа Чума ХХ века- СПИД.
Чума ХХ века- СПИД. Конкурс презентаций «Скажи здоровью – Да» СКАЖИ ЗДОРОВОМУ ОБРАЗУ ЖИЗНИ – ДА, А ВРЕДНЫМ ПРИВЫЧКАМ – НЕТ!!! Выполнил: Федоров Д.А., уч
Конкурс презентаций «Скажи здоровью – Да» СКАЖИ ЗДОРОВОМУ ОБРАЗУ ЖИЗНИ – ДА, А ВРЕДНЫМ ПРИВЫЧКАМ – НЕТ!!! Выполнил: Федоров Д.А., уч Учительская династия Кутюхиных
Учительская династия Кутюхиных Кадетские классы МОУ «средняя школа № 5» г.Петрозаводсккадетскому движению – 5 лет!
Кадетские классы МОУ «средняя школа № 5» г.Петрозаводсккадетскому движению – 5 лет!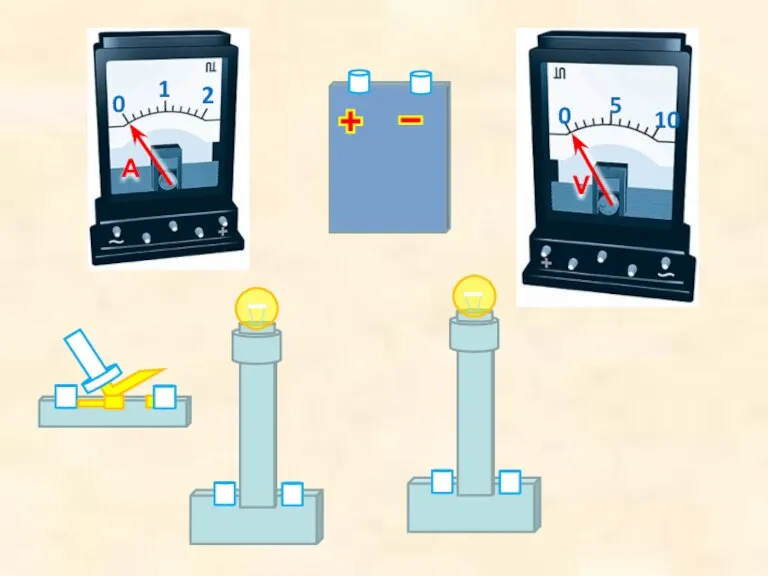 Последовательное соединенье проводников
Последовательное соединенье проводников Презентация на тему Историко-цивилизационная концепция культуры А. Тойнби
Презентация на тему Историко-цивилизационная концепция культуры А. Тойнби  EXPERT
EXPERT Реализация проекта «Кто не умеет говорить, тот карьеры не сделает» (Повышение речевой компетенции учащихся как основа их успешно
Реализация проекта «Кто не умеет говорить, тот карьеры не сделает» (Повышение речевой компетенции учащихся как основа их успешно энн
энн Давайте познакомимся…
Давайте познакомимся… Презентация дипломной работы на тему «Учёт и анализ финансовых результатов (на материалах ОАО «Бобруйскагромаш», г. Бобруйск)»
Презентация дипломной работы на тему «Учёт и анализ финансовых результатов (на материалах ОАО «Бобруйскагромаш», г. Бобруйск)» « Мы из СССР »
« Мы из СССР » НАРКОТИКИ-дорога к смерти.
НАРКОТИКИ-дорога к смерти. Правовое государство
Правовое государство Презентация на тему Кожно-мышечная чувствительность. Обоняние. Вкус
Презентация на тему Кожно-мышечная чувствительность. Обоняние. Вкус Система ФОССТИС в индустрии
Система ФОССТИС в индустрии Писатели России
Писатели России Вторая жизнь Храма городца Ижеславец
Вторая жизнь Храма городца Ижеславец Работа с табелем
Работа с табелем Обучение заработку в интернете
Обучение заработку в интернете