Содержание
- 2. ЦЕЛИ: Познакомиться с основными понятиями комбинаторики и методами решения комбинаторных задач.
- 3. СТРУКТУРА: Комбинаторика: содержание материала примеры Множества и операции над ними: содержание материала упражнения Основные законы комбинаторики:
- 4. Комбинаторика – один из разделов математики, играющий важную роль при решении некоторых современных проблем теории вероятностей,
- 5. Приведем примеры комбинаторных задач: 1. Узнать, сколькими способами можно из 7 мальчиков и 9 девочек выбрать
- 6. В жизни человеку часто приходится объединять предметы в группы и для каждой группы придумывать особые названия:
- 7. Множество может содержать любое количество элементов. Если множество содержит конечное число элементов, то оно называется конечным
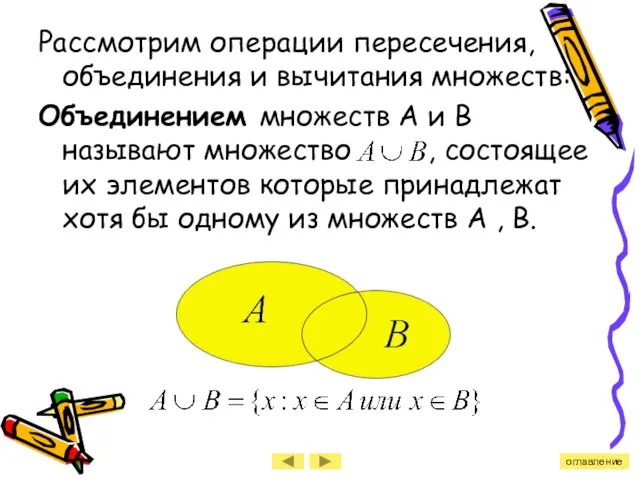
- 8. Рассмотрим операции пересечения, объединения и вычитания множеств: Объединением множеств А и В называют множество , состоящее
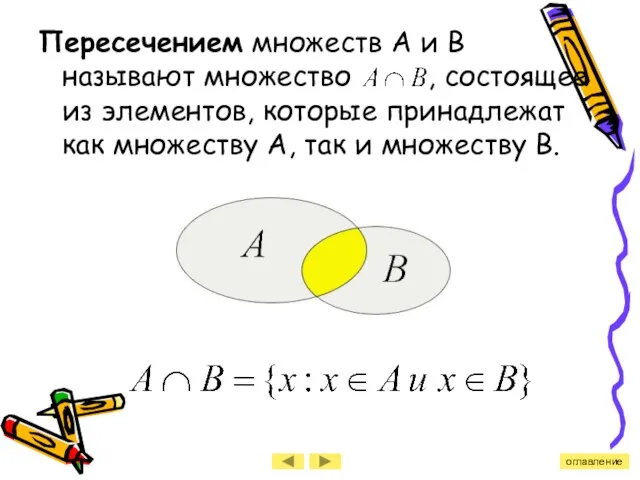
- 9. Пересечением множеств А и В называют множество , состоящее из элементов, которые принадлежат как множеству А,
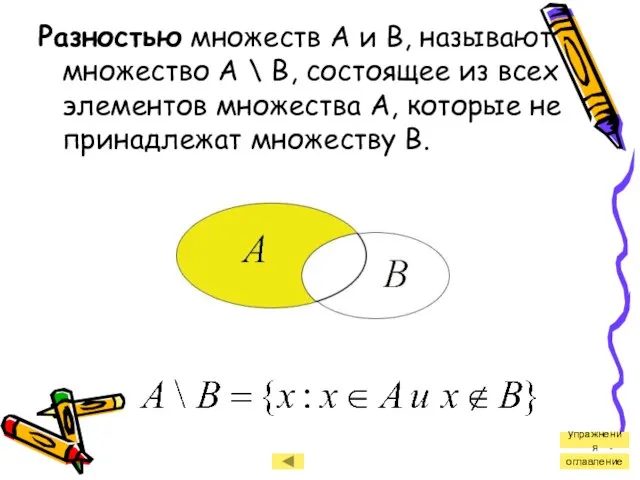
- 10. Разностью множеств А и В, называют множество А \ В, состоящее из всех элементов множества А,
- 11. Упражнения: Даны множества А = {1;2;3;4;5} и B = {3;4;5;6;7}. Найти: 1) 2) 3) Ответы: 1)
- 12. Часто приходится рассматривать упорядоченные множества, т.е. множества, в которых каждый элемент занимает свое, вполне определенное место.
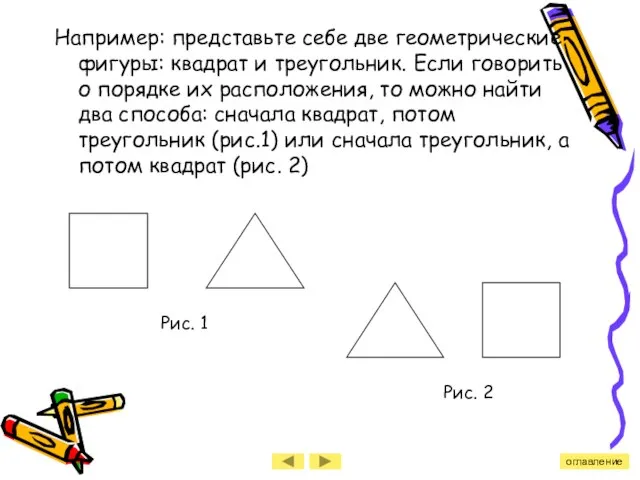
- 13. Например: представьте себе две геометрические фигуры: квадрат и треугольник. Если говорить о порядке их расположения, то
- 14. Точно также множество, состоящее их трех элементов a, b, c можно упорядочить шестью способами: (a b
- 15. Можно доказать, что число перестановок из четырех элементов равно 24,т.е. Аналогично и т.д. Тогда число перестановок
- 16. Если каждый элемент множества А является в то же время и элементом множества В, то говорят,
- 17. Каждое упорядоченное подмножество множества А называют размещением. Например: сколькими способами можно выбрать четырех человек на различные
- 18. Можно заметить, что тот же результат буден получен, если размещения связать с перестановками, т.е. Рассуждая аналогичным
- 19. Размещения – это упорядоченные подмножества данного множества, которые отличаются друг от друга не только выбором элементов,
- 20. Например: в классе 10 юношей-допризывников. Сколькими способами они могут выбрать четверых для участия в слете ДОСААФ?
- 21. Упражнения: 1) Вычислите: 2) Вычислите: 3) Сколькими способами можно рассадить 8 человек на восьми свободных стульях?
- 22. Решение: 1) = «
- 23. Решение: 2) = = «
- 24. Решение: 3)Чтобы вычислить сколько способов существует для того чтобы рассадить 8 человек на восьми свободных стульях
- 25. Упражнения: 1) Вычислите: Вычислите: 3) Решите уравнение: 4) Сколькими способами могут быть присуждены золотая, серебряная и
- 26. Решение: 1) = = «
- 27. Решение: 2) = «
- 28. Решение: 3) Решить уравнение , значит найти значение переменной х. Т.е. , тогда ; , учитывая
- 29. Решение: 4) Каждый выбор трех медалистов из 11 участников отличается друг от друга составом и порядком
- 30. Упражнения: 1) Вычислите: 2) Вычислите: 3) Сколько прямых можно провести через 7 точек, из которых никакие
- 31. Решение: 1) = = «
- 32. Решение: 2) = «
- 33. Решение: 3) Каждые две точки определяют одну прямую, и при этом не играет роли в каком
- 34. Проверь себя! 1). Сколькими способами можно разместить 6 человек на одной скамейке? 2). Учащиеся изучают 10
- 35. Для решения многих комбинаторных задач и доказательства формул применяются следующие правила комбинаторики: 1). Правило суммы: Если
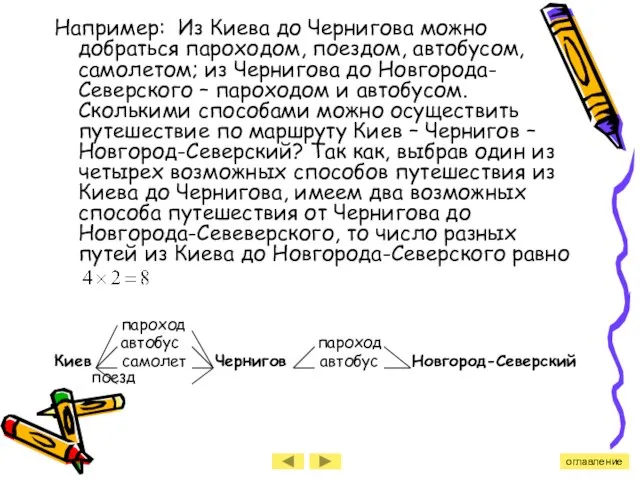
- 36. Например: Из Киева до Чернигова можно добраться пароходом, поездом, автобусом, самолетом; из Чернигова до Новгорода-Северского –
- 37. 3). Метод математической индукции: Если некоторое утверждение относительно натурального числа n верно для n=1 и из
- 38. Например: докажите, что сумма первых n нечетных чисел равна , т.е. 1+3+5+7+ …+(2n-1)= Решение: проверим справедливость
- 39. Упражнения: 1) докажите, что сумма первых чисел натурального ряда равна . решение оглавление теория
- 40. Доказать, что Решение: - при n = 1 формула верна: - предположим, что формула верна для
- 44. Скачать презентацию
















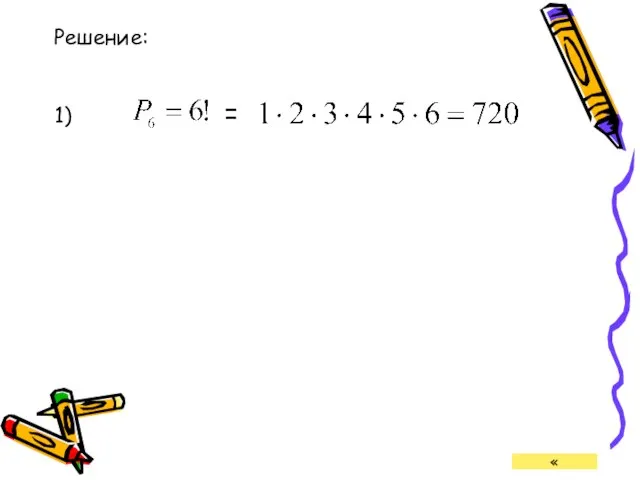
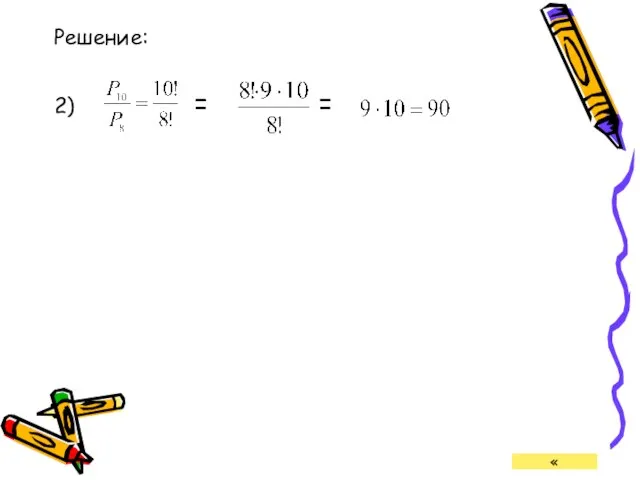


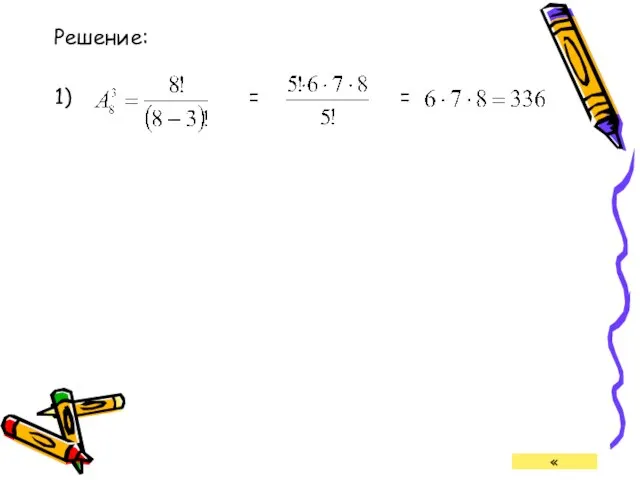
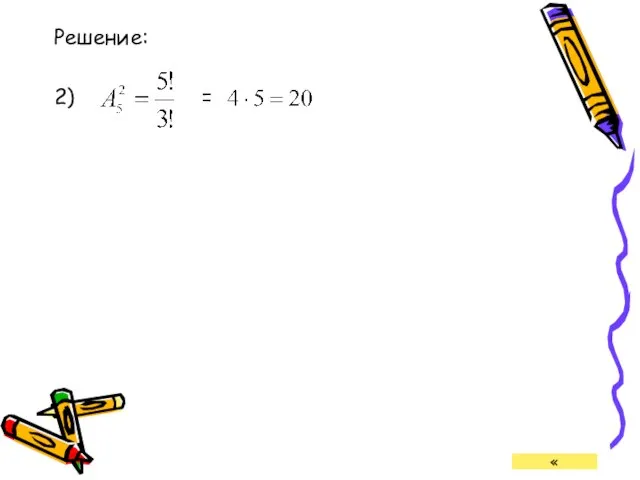



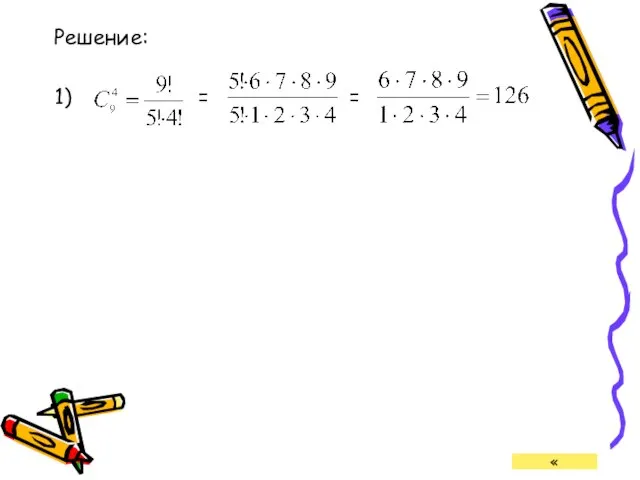
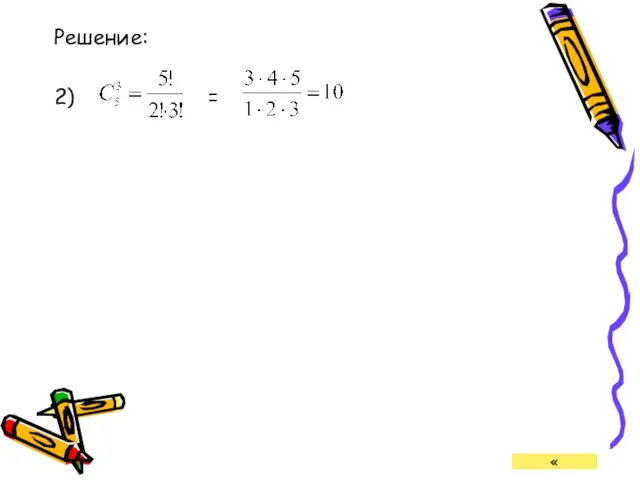









 Обмен первичными документами в электронном виде
Обмен первичными документами в электронном виде Генные технологии и биоэтика
Генные технологии и биоэтика ЛЕКЦИЯ 4. ПОТОК БИОИНФОРМАЦИИ в КЛЕТКЕ – ПОСТТРАНСКРИПЦИОННЫЕ ПРОЦЕССЫ. ФУНКЦИОНАЛЬНАЯ ХАРАКТЕРИСТИКА ГЕНОВ. ТРАНСЛЯЦИЯ и ПОСТТР
ЛЕКЦИЯ 4. ПОТОК БИОИНФОРМАЦИИ в КЛЕТКЕ – ПОСТТРАНСКРИПЦИОННЫЕ ПРОЦЕССЫ. ФУНКЦИОНАЛЬНАЯ ХАРАКТЕРИСТИКА ГЕНОВ. ТРАНСЛЯЦИЯ и ПОСТТР Формулы сокращённого умножения
Формулы сокращённого умножения Разработка системы управления прибылью и рентабельностью государственной организации ГАУК Новокузнецкий драматический театр
Разработка системы управления прибылью и рентабельностью государственной организации ГАУК Новокузнецкий драматический театр Воины-интернационалисты
Воины-интернационалисты Нарушения. Правила и нормы технической эксплуатации жилищного фонда
Нарушения. Правила и нормы технической эксплуатации жилищного фонда В мире профессий
В мире профессий Изучение влияния роли сбалансированного питания на здоровье человека
Изучение влияния роли сбалансированного питания на здоровье человека Детский церебральный паралич
Детский церебральный паралич  Радиоактивность - мифы и реальность
Радиоактивность - мифы и реальность Порядок сертификации строительных, дорожных и коммунальных машин
Порядок сертификации строительных, дорожных и коммунальных машин От ар деко до аэростиля. От кубизма - к функционализму
От ар деко до аэростиля. От кубизма - к функционализму Презентация на тему ЭСТОНИЯ (11 класс)
Презентация на тему ЭСТОНИЯ (11 класс)  Новое слово на рынке корпоративных сувениров и промо-материалов ПРОДУКЦИЯ Новый вид корпоративных сувениров – кожные антисептик
Новое слово на рынке корпоративных сувениров и промо-материалов ПРОДУКЦИЯ Новый вид корпоративных сувениров – кожные антисептик Второв Н.А.
Второв Н.А. Светлой памяти А. Миронова. Все главы
Светлой памяти А. Миронова. Все главы Универсальный пульсирующий маяк
Универсальный пульсирующий маяк Источники права
Источники права Медициналық сақтандыру
Медициналық сақтандыру Обучение грамоте
Обучение грамоте Акция Ангстрем. Участники РТТ и ОПТ Сыктывкар и районы, Ухта и районы, Филиалы Печора, Усинск, Инта
Акция Ангстрем. Участники РТТ и ОПТ Сыктывкар и районы, Ухта и районы, Филиалы Печора, Усинск, Инта MIMIO 6.11 RUS
MIMIO 6.11 RUS Комплексная экспедиция Лицея 15532006 г., июль-август
Комплексная экспедиция Лицея 15532006 г., июль-август Все порадуйтесь за нас, перешли мы в 5 класс!
Все порадуйтесь за нас, перешли мы в 5 класс! Кукла-оберег Благополучница
Кукла-оберег Благополучница Позвони мне, позвони…
Позвони мне, позвони… Начальные этапы
Начальные этапы