Тема: Моделирование физических явлений при помощи пакета Mathematica

Основные классы данных
Mathematica оперирует с тремя основными классами данных:
численными данными, представляющими числа различного вида;
символьными данными, представляющими символы, тексты и математические выражения (формулы);
списками — данными в виде множества однотипных или разнотипных данных.

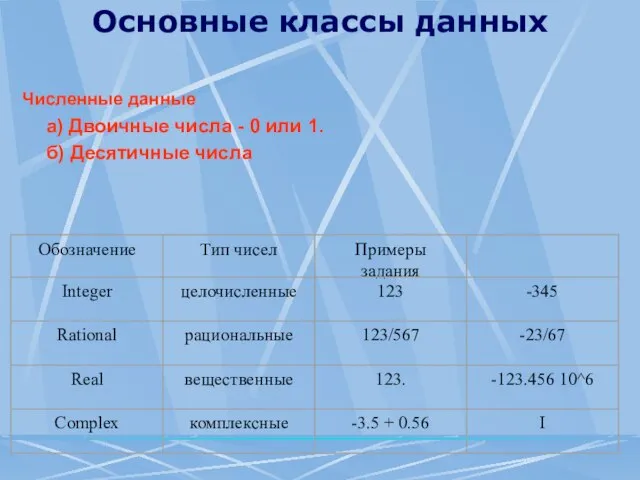
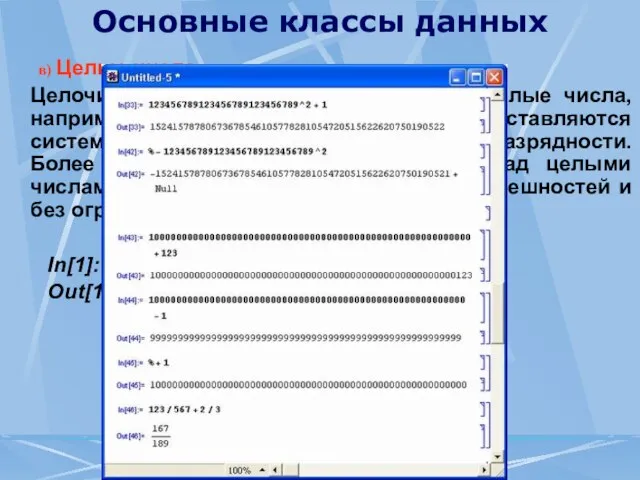
Основные классы данных
Численные данные
а) Двоичные числа - 0 или 1.
б) Десятичные числа

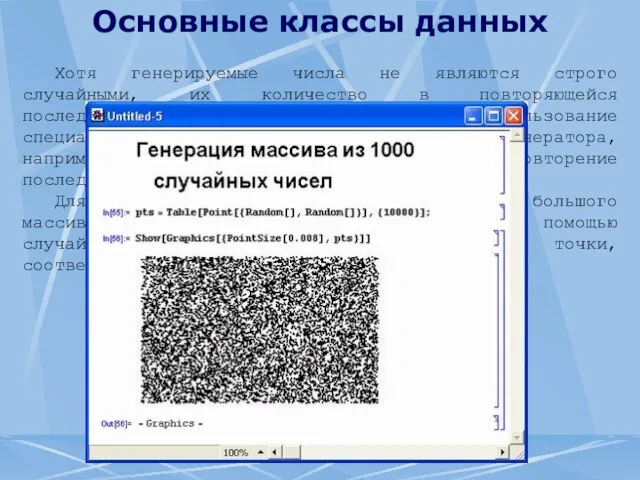
Основные классы данных
в) Целые числа
Целочисленные данные (Integer) — это целые числа, например 1, 2 или 123, которые представляются системой без погрешности и ограничения разрядности. Более того, арифметические операции над целыми числами система выполняет также без погрешностей и без ограничения числа цифр.
In[1]:= 20!+5!
Out[1]= 20274183401472001

Основные классы данных
г) Данные вещественного типа
Численные данные можно представить также десятичными вещественными числами, которые могут иметь различную форму, например, 123.456, 1.234*10^2, 12345.6 10^-2 и т.д. В общем случае они содержат мантиссу с целой и дробной частями и порядок, вводимый как степень числа 10. Выражение с порядком выделяется из мантиссы знаком умножения – либо пробелом, либо звездочкой *. В вводе для возведения в степень используется символ ^, но стандартный вывод задает порядок с применением чисел порядка в отдельной строке над мантиссой. Например:
In[1]:= 23.456*10^100
Out[1]= 1.23456 10102
In[2]:= N[Sin[1]]
Out[2]= 0.841471

Основные классы данных
Mathematica производит операции с числами изначально как с целыми. Однако установка значка разделительной точки означает, что число должно рассматриваться как вещественное. Например, 1 — целое число, но 1. — уже вещественное число.
Для представления выражения expr в форме вещественного числа используется функция
N [expr] или N [expr, число_цифр_результата].
N[2*Pi,50]
6.283185307179586476925286766559005768394338

Основные классы данных
Функции IntegerPart [x] и FractionalPart [x] обеспечивают возврат целой и дробной частей вещественного числа х:
N[Pi]
3.14159
IntegerPart[Pi]
3
FractionalPart[Pi]
-3.+ Л
N[FractionalPart[Pi]]
0.141593
Функция RealDigits [x] возвращает список реальных цифр результата и число цифр целой части х:
RealDigits[N[2*Pi]]
{{6, 2, 8, 3, 1, 8, 5, 3, 0, 7, 1, 7, 9, 5, 8, 6}, 1}

Основные классы данных
д) Комплексные числа
Многие математические операции базируются на понятии комплексных чисел, имеющих действительную и мнимую части. Они задаются в форме
z=Re(z)+I*Im(z) или z=Re(z)+i Im(z)
где знак I - мнимая единица (квадратный корень из -1), Re(z) - действительная часть комплексного числа, a Im(z) - мнимая часть.
2+I*3 или 2+3I
Мнимая часть задается умножением ее значения на символ мнимой единицы I – (или i). При этом знак умножения * можно указывать явно или заменить пробелом. Части комплексного числа могут быть целыми, вещественными и рациональными числами.

Основные классы данных
е) Cимвольные данные и строки
Символьные данные в общем случае могут быть отдельными символами (пример a, b,...,z), строками (strings) и математическими выражениями expr (от expression - выражение), представленными в символьном виде. Символьные строки задаются цепочкой символов в кавычках, например, 0 “ssss”, и являются строчными объектами.
\n— новая строка (line feed);
\ t — табуляция.
Примеры:
"Hello my friend!"
Hello my friend!
"Hello\nmy\nfriend!"
Hello
my
friend!
"Hello\tmy\tfriend!"
Hello my friend;

Основные классы данных
ж) Выражения
Выражения в системе Mathematica обычно ассоциируются с математическими формулами, например:

Основные классы данных
Для записи математических выражений используются как операторы, так и функции. Тонкости синтаксиса системы, используемого при записи арифметических операций
следующие:
1. знак умножения может быть заменен пробелом;
2. встроенные функции начинаются с прописной буквы и обычно повторяют свое общепринятое математическое обозначение;
3. круглые скобки () используются для выделения частей выражений и задания приоритета при их выполнении;
4. параметры функций задаются в квадратных скобках [];
5. фигурные скобки {} используются при задании списков.

Основные классы данных
з) Списки и массивы
Наиболее общим видом сложных данных в системе являются списки (иногда их называют листами) Списки представляют собой совокупность однотипных или разнотипных данных, сгруппированных с помощью фигурных скобок.

Основные классы данных
Объекты и идентификаторы
В общем случае система Mathematica оперирует с объектами. Под ними подразумеваются математические выражения (expr), символы (symbols), строки из символов (strings), упомянутые выше числа различного типа, константы, переменные, графические и звуковые объекты и т. д.
Каждый объект характеризуется своим именем — идентификатором. Это имя должно быть уникальным, то есть единственным. Существуют следующие правила задания имен:
sssss — имя объекта, заданного пользователем;
Sssss — имя объекта, входящего в ядро системы;
$Sssss — имя системного объекта.

Основные классы данных
Константы
Константы являются типовыми объектами системы, несущими заранее предопределенное численное или символьное значение. Это значение не должно меняться по ходу выполнения документа. К численным константам относятся любые числа, непосредственно используемые в математических выражениях или в программных объектах, например, в процедурах и функциях. Используются следующие поименованные константы:

Основные классы данных
Переменные
Переменные - это объекты, которые могут принимать различные значения, находящиеся в определенном допустимом множестве значений.
Переменным обычно присваиваются имена- идентификаторы.
var=value
var - имя переменной; value - ее значение.
Основные операции по присвоению переменным их значений в упрощенной форме:

Основные классы данных
Примеры по присвоению значений переменной:

Основные классы данных
Функции системы
Функцией в системе Mathematica называют объект, который задается своим именем и списком формальных параметров в квадратных скобках и возвращает в ответ на обращение к нему по имени с указанием списка фактических параметров, некоторый результат. Он может иметь тип числа, строчного выражения или математического выражения - формулы.
Под это определение попадает множество хорошо известных функций, например, алгебраические ln(x) или exp(x), тригонометрические sin(x), cos(x) и т.д. На языке Mathematica они записываются как Ln[x], Exp[x], Sin[x], Cos[x] и т.д.
В общем виде функцией является объект вида:
Идентификатор_функции[о1,о2,о3,…]
Здесь о1, о2, о3,… - объекты-параметры, которые могут быть числами, константами, списками, математическими выражениями, символами, строками, математическими выражениями, символами, строками, опциями и т.д. (Таблица 1).

Основные классы данных
Таблица 1. Математические функции в системе Mathematica
In[1]:= Fun[x_]:=Exp[x]-1
N[Fun[1.0],10]
Out[1]= 1.718281828

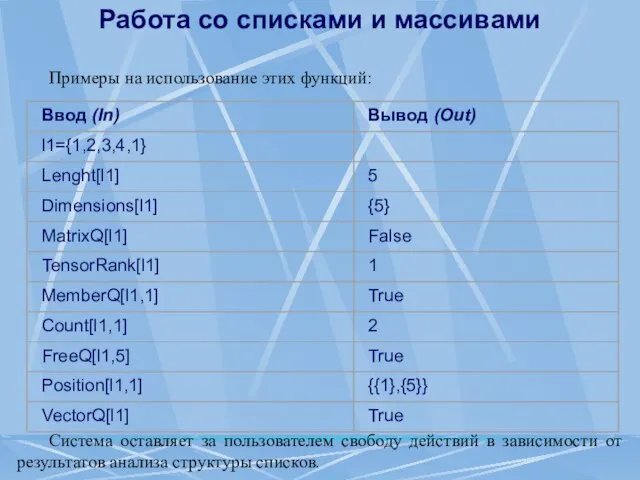
Основные классы данных
Функции генерации случайных чисел
Для реализации статистических методов моделирования используются случайные числа. Система имеет генератор псевдослучайных чисел, доступ к которому обеспечивают следующие функции:
Random [ ] — возвращает равномерно равномерно распределенное псевдослучайное число типа Real в интервале от 0 до 1;
Random [type, range] — дает псевдослучайное число указанного типа type, лежащее в указанном интервале range. К возможным типам относятся Integer, Real и Complex. По умолчанию принят интервал от 0 до1. Можно задать интервал явно в виде {min, max}; спецификация интервала в виде max эквивалентна {0, max};
SeedRandom[n] — сбрасыывает (устанавливает в начальное состояние) генератор случайных чисел, используя целое n как начальное число;
SeedRandom [ ] — устанавливает генератор, используя в качестве начальнго числа текущее время.

Основные классы данных
Хотя генерируемые числа не являются строго случайными, их количество в повторяющейся последовательности очень велико. Использование специальной установки начального состояния генератора, например по времени дня, делает повторение последовательности практически невозможным.
Для проверки равномерности распределения большого массива случайных чисел можно задать с их помощью случайные координаты и затем построить точки, соответствующие координатам (х, у).

Основные классы данных
Выполнение арифметических операций
Для выполнения простых арифметических операций достаточно набрать необходимое математическое выражение и нажать Enter (справа)
а) арифметические вычисления
In[1]:= N[Sin[1]]
Out[1]= 0.841471
In[2]:= 2+2
Out[2]= 4
б) использование результатов предыдущих вычислений (%)
% - возвращает результат последней предшествующей операции
%% - возвращает результат операций выполненной перед последней предшествующей операцией.
In[3]:= %+4
Out[3]= 8

Основные классы данных
в) вывод результатов вычислений
Большинство функций системы возвращают результат в символьном виде.
In[4]:= Sin[1]
Out[4]= Sin[1]
Функция с однобуквенным названием N[expr] дает численное вещественное значение (аппроксимацию) для любого выражения expr (expression - выражение), которое имеет численное значение. N[Sin[1]]
Также можно задать вычисление любого выражения с выводом результатов в форме вещественного числа, используя expr//
In[5]:= 1/3+2/7
Out[5]=
In[6]:= 1/3+2/7//N
Out[6]= 0.619048

Основные классы данных
г) арифметические вычисления с повышенной точностью Rationalize[x] и Rationalize[x,dx] дают приближение для числа х в виде рациональных чисел. Вторая из этих функций задает приближение с заданной точностью.
In[7]:= Rationalize[N[Pi],10^-3]
Out[7]=

Работа со списками и массивами
Списки и их свойства
Часто математические или иные объекты содержат множество данных, которые желательно объединять под заданным именем.
Например, под объектом с именем М можно подразумевать квадратную матрицу 10×10 элементов с их общим числом 100.
Для объединения данных используются списки или листы (список - по английски list).
Mathematica имеет обширные возможности работы со списками, содержащими не только однотипные, но и разнотипные данные – элементы. На языке системы список – это совокупность данных, указанных в фигурных скобках, например:
{1,4,2,7,9} или {a,b,c,d,e}
Списки можно составлять напрямую, задавая объекты в соответствии с описанным синтаксисом. Однако можно и генерировать некоторые виды списков, таких , как таблицы или массивы.

Работа со списками и массивами
Генерация списков
Для генерации списков с элементами - вещественными и целыми числам или даже целыми выражениями - особенно часто используется функция Table, создающая таблицу - список.

Работа со списками и массивами
Примеры на использование функции Table:

Работа со списками и массивами
Применяется также функция Range для создания ранжированных числовых элементов, значения которых лежат в некотором диапазоне числовых значений.
Примеры на использование функции Range:

Работа со списками и массивами
Выделение и вывод элементов списков.
Списки представляли бы малую ценность, если бы не было средств выделения любых элементов из них. Но такие средства есть. Для выделения элементов списка используются двойные квадратные скобки.

Работа со списками и массивами
Для вывода элементов списка используется функция TableForm с рядом опций:

Работа со списками и массивами
Эти же опции используются и для функции MatrixForm[list], служащей для вывода матриц. Эта функция печатает элементы списка list следующим образом: каждый элемент списка заключен в квадратную ячейку одинакового с другими размера.
Одноуровневый список печатается в виде столбца, а двухуровневый - в стандартной матричной форме.
Векторы и матрицы являются разновидностью списков, причем векторы – это одномерные массивы, а матрицы – двумерные.

Работа со списками и массивами
Выявление структуры списков
Списки относятся к данным сложной структуры. Поэтому при работе с ними возникает необходимость контроля за структурой списков, без чего их применение может привести к грубым ошибкам – как явным, сопровождаемым выдачей сообщения об ошибке, так и неявным.
Для выявления структуры списков используется ряд функций:

Работа со списками и массивами
Примеры на использование этих функций:
Система оставляет за пользователем свободу действий в зависимости от результатов анализа структуры списков.

Работа со списками и массивами
Работа со списком в стеке
Элементы списков могут размещаться в так называемом стеке.
Стек – это особая структура хранения данных, чисто умозрительно напоминающая стопку тарелок в шкафу. В нашем примере тарелки – это данные. Очередную «тарелку» можно положить только сверху – на вершину стека. На дне стека лежит первая введенная в него «тарелка». Стек подчиняется правилу: последнее введенное данное извлекается первым, а первое введенное данное извлекается последним. Стек относится к системам хранения данных динамического типа – его размеры непрерывно меняются по ходу вычислений. Стек может быть и пустым, если из него были извлечены все данные.

Работа со списками и массивами
Работа со стеком
Система Mathematica имеет обширный набор функций для операций со стеком. Приведем эти функции:

Работа со списками и массивами
Пояснить работу со стеком могут следующие примеры:

Работа со списками и массивами
Включение в список новых элементов
Mathematica дает ряд расширенных возможностей для работы со списками. Для расширения списка путем включения в него новых элементов используются следующие функции:
Примеры, которые иллюстрируют применение этих функций:

Работа со списками и массивами
Изменение порядка расположения элементов в списке
Помимо добавления в список новых данных имеется возможность изменения порядка расположения данных в списке. Она реализуется следующими операциями:

Работа со списками и массивами
Примеры на использование этих функций:

Работа со списками и массивами
Иногда возникает необходимость комбинирования нескольких списков. Для этого используются операции:
Приведем примеры:

Работа со списками и массивами
Для работы со списками используются также следующие, менее распространенные функции.

Работа со списками и массивами
Массивы - списки
Совокупность данных образует массив (Array). Массивы могут быть одномерными (один список), двумерными и многомерными (два списка и более). Одномерные массивы в математике называют векторами, двумерные - матрицами. Mathematica позволяет создавать многомерные массивы - число элементов в них ограничено лишь объемом памяти компьютера.
Для задания массивов используются следующие функции:

Работа со списками и массивами
Примеры задания массивов и их вывода:

Работа со списками и массивами
Функции для операции с массивами
Основные операции над массивами и матрицами позволяет осуществить следующая группа функций:

Работа со списками и массивами
Примеры применения основных из этих функций:

Расширенные математические возможности
Суммы и произведения
Маthematica обладает широкими возможностями в реализации расчетов, относящихся к различным разделам математического анализа. В частности, система позволяет вычислять суммы и произведения вида:
В этих операциях суммируются или перемножаются значения некоторой функции fi . Управляющая переменная i в общем случае принимает значения от минимального (начального) imin до максимального (конечного) imax с шагом равным di. При целочисленных значениях i эта переменная называется индексной и прямо указывает на индекс соответствующего элемента ряда.

Расширенные математические возможности
Вычисление сумм
Для вычисления сумм в системе предусмотрен ряд функций:

Расширенные математические возможности
Приведем примеры использования основных функций суммирования:
Таким образом, эти функции обеспечивают расширенные
возможности вычисления сумм - как при целочисленных, так и
вещественных значениях управляющих переменных переменных,
задающих циклы вычислений.

Расширенные математические возможности
Вычисление произведений
Операции вычисления произведений представлены следующими функциями:

Расширенные математические возможности
Примеры использования функций вычисления произведения:

Расширенные математические возможности
Вычисление производных
К числу наиболее часто используемых математических операций принадлежит вычисление производных функций f(x)
как в аналитической, так и в символьной форме. Для этого используются следующие функции:

Расширенные математические возможности

Расширенные математические возможности
Примеры вычисления производных:

Расширенные математические возможности
Вычисление первообразных и определенных интегралов
Для вычисления интегралов в системе используются следующие функции:

Расширенные математические возможности
Для обозначения реальных пределов используется константа Infinity, означающая положительную бесконечность. Пределы могут задаваться как константами так и функциями.

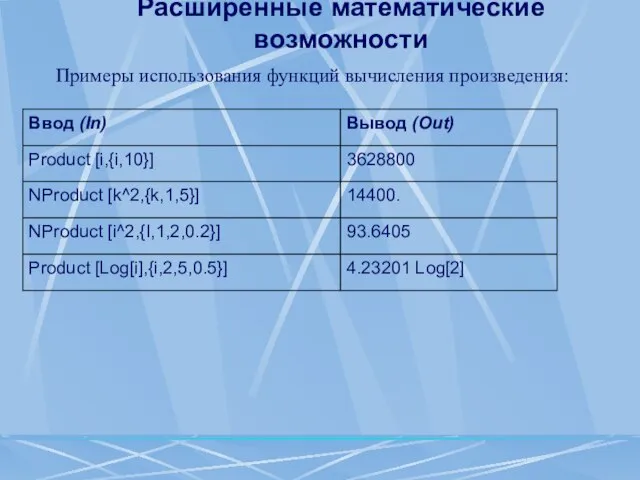
Расширенные математические возможности
Для вычисления численных значений определенных интегралов используется функция
NIntegrate[f,{x,xmin,xmax}]
Она возвращает приближенное значение интеграла от функции f по переменной х в интервале от xmin до xmax.
NIntegrate[,{x,0.5,2}]

Расширенные математические возможности
Вычисление пределов функций
Система Mathematica не только вычисляет пределы функций, заданных аналитически, в виде числа, но и позволяет найти предел в аналитическом виде. Для этого используется функция
Limit[expr,x->x0].
Она ищет значение предела выражения expr при х, стремящемся к 0.

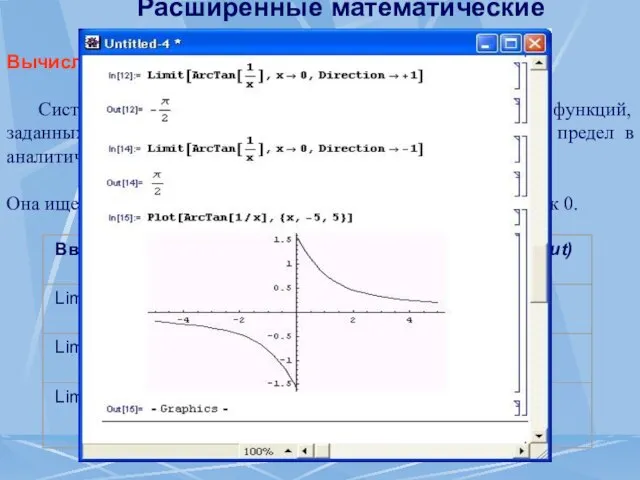
Расширенные математические возможности
При работе с функцией Limit используются следующие опции:
Применение этих опций может оказаться полезным в сложных случаях вычисления пределов.

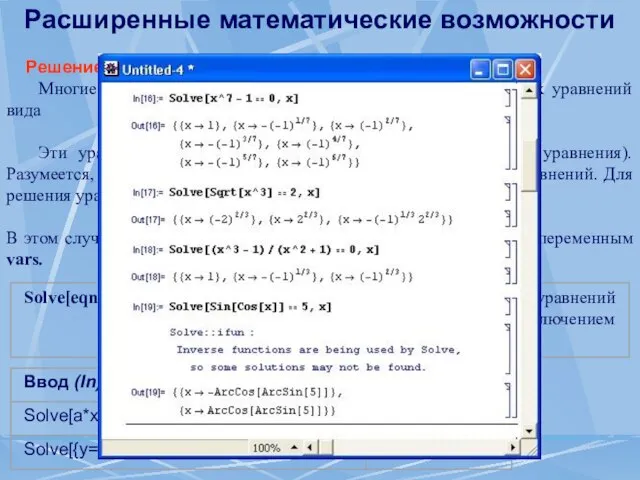
Расширенные математические возможности
Решение уравнений
Многие математические задачи сводятся к решению нелинейных уравнений вида
f(x)=0 или f(x)=expr
Эти уравнения обозначаются как eqns (от слова equations - уравнения). Разумеется, могут решаться и системы, состоящие из ряда таких уравнений. Для решения уравнений в символьном виде система имеет функцию
Solve[eqns,vars]
В этом случае функция пытается найти решение уравнений eqns по переменным vars.

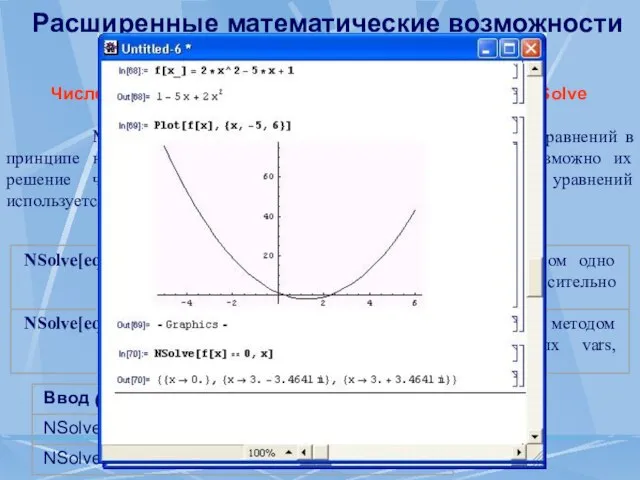
Расширенные математические возможности
Численное решение уравнений с помощью функции NSolve
Многие нелинейные уравнения и системы нелинейных уравнений в принципе не имеют аналитических решений. Однако вполне возможно их решение численными методами. Для численного решения уравнений используется следующая функция:

Расширенные математические возможности
Решение дифференциальных уравнений в символьном виде
Дифференциальными уравнениями принято называть уравнения, в состав которых входят производные функции y(x), представляющей решение уравнения. Дифференциальные уравнения могут быть представлены в различной форме, например в общеизвестной форме Коши
Несколько взаимосвязанных дифференциальных уравнений образуют систему.
Для решения дифференциальных уравнений в символьном виде используются следующие средства:

Расширенные математические возможности
Приведем примеры решения дифференциальных уравнений:

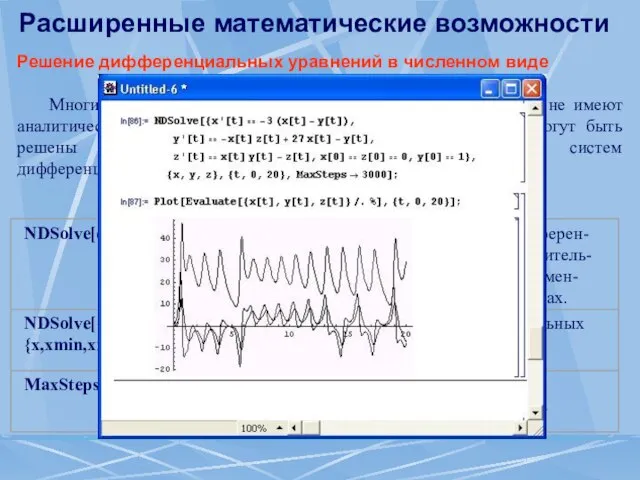
Расширенные математические возможности
Решение дифференциальных уравнений в численном виде
Многие дифференциальные уравнения, например нелинейные, не имеют аналитических решений. Однако они с приемлемой точностью могут быть решены численными методами. Для численного решения систем дифференциальных уравнений используется функция NDSolve.

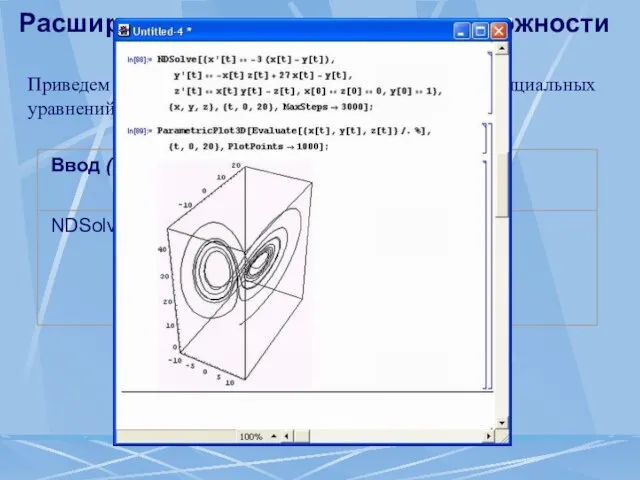
Расширенные математические возможности
Приведем пример решения системы из трех дифференциальных уравнений:

Расширенные математические возможности
Функции минимизации и максимизации
В практике прикладных математических вычислений важная роль принадлежит оптимизационным задачам, например таким, как поиск минимальных и максимальных значений функции одной или ряда переменных. Система Mathematica дает разнообразные возможности по решению задач оптимизации – от поиска элементов списка с минимальным или максимальным значением до поиска локальных или даже глобальных минимумов функции, заданных аналитически.
Для поиска максимального и минимального значений ряда чисел, входящих в список имеются следующие функции:

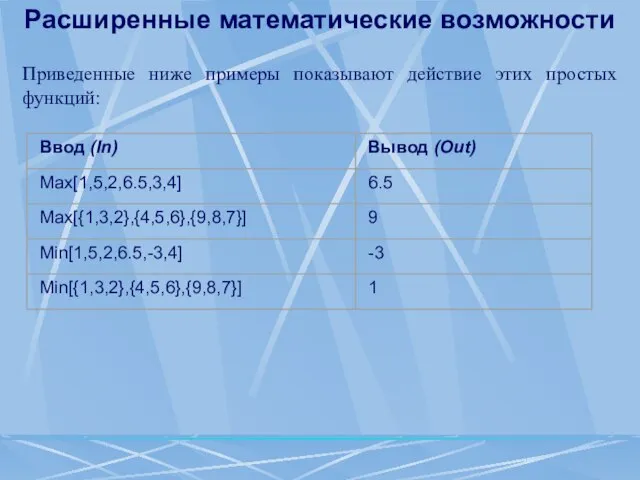
Расширенные математические возможности
Приведенные ниже примеры показывают действие этих простых функций:

Расширенные математические возможности
Для поиска локального минимума некоторой аналитической функции f(x) используется функция:
Приведем примеры применения функции FindMinimum :

Расширенные математические возможности
Для поиска глобального максимума и минимума аналитически заданной функции ряда переменных служат следующие две функции:
Эти функции решают типовые задачи линейного программирования. В дополнение к ним может быть использована функция:

Расширенные математические возможности
К задачам на минимизацию относятся также задачи линейной и нелинейной регрессии. В них вычисляются параметры некоторой функции, при которых среднеквадратичная погрешность между результатами вычислений по этой функции и совокупностью исходных данных минимальна. В отличие от интерполяции при регрессии данная функция в узловых точках не дает точного значения ординат – она просто минимизирует в них погрешности вычислений.
Для решения таких задач используется функция Fit.
Fit[data,func,vars]
Для списка данных data она ищет приближения методом наименьших квадратов в виде линейной комбинации функций funs переменных vars. Данные data могут иметь форму {{x1,y1,…,f1},{x2,y2,…,f2},…}, где число координат x,y,… равно числу переменных в списке vars. Они могут быть представлены также в форме {f1,f2,…} с одной координатой, принимающей значения 1,2,… Аргумент funs может быть любым списком функций, которые зависят только от объектов vars.

Расширенные математические возможности
Следующие примеры показывают приближение исходных данных степенным полиномом и линейной комбинацией двух функций:

Расширенные математические возможности
Символьные операции. Работа с выражениями.
Одним из важнейших понятий системы является математическое выражение, или просто выражение - expr (от слова expression). Выражение может быть представлено в общепринятом виде (как математическая формула или ее часть) с помощью операторов, например: a*(x+y+z) или х^y; оно может задавать и некоторую функцию f[x,y,...]. Наряду с такой формой существует так называемая полная форма представления выражений, при которой основные арифметические операции задаются не операторами, а только соответствующими функциями. Фактически именно с выражениями, представленными в полной форме, оперирует символьное ядро системы.
В системе предусматривается различная работа с выражениями (сложение, умножение, возведение в степень, создание списка и т.д.

Расширенные математические возможности
Упрощение выражений
Упрощение математических выражений - одна из самых важных задач символьной математики. Порою невероятно сложное математическое выражение (которое пугает с первого вида) является просто нулем или единицей либо сводится к простому выражению после ряда преобразований. Качество выполнения операции упрощения во многом определяется мощью ядра математической системы, поскольку зависит от числа функций и правил преобразования выражений, заложенных в ее символьное ядро.
Для упрощения выражений используется функция Simplify:

Расширенные математические возможности
Функции раскрытия и расширения выражений
Расширение или раскрытие выражений - еще одна типовая операция компьютерной алгебры. Часто компактная форма представления выражений обусловлена определенными операциями по их упрощению. Существует множество выражений, для которых эти правила известны.
Например:

Расширенные математические возможности
Основные функции, возвращающие результаты с раскрытием и расширением выражений:

Расширенные математические возможности
Примеры:

Расширенные математические возможности
К операциям, расширяющим выражения относятся также функции:
Примеры:

Расширенные математические возможности
Функции для расширенных операций с выражениями
Мы рассмотрели немногочисленную группу функций для работы с выражениями: их упрощения, расширения, выделения множителей и т.д. Эти функции способны решать большинство повседневных задач, связанных с аналитическими преобразованиями выражений. Однако система имеет гораздо более полный набор функций для работы с выражениями.
Для расширенной работы с выражениями служат следующие функции:

Расширенные математические возможности
Примеры:

Графические возможности пакета Mathematica
Графика всегда была козырной картой системы. Графические возможности достигаются как обилием встроенных функций, так и средствами их модификации с помощью директив, опций и примитивов. Система позволяет строить практически любые виды математических графиков, причем обычного пользователя в большинстве случаев удовлетворяют графики, параметры которых система задает по умолчанию.
Начнем рассмотрение графических возможностей системы с построения графиков функций одной переменной вида y = f(x) или просто f(x). График таких функций строится на плоскости, т.е. в двумерном пространстве. Он представляет собой геометрическое место точек (y,x) при изменении независимой переменной х (абциссы) в заданных пределах, например от минимального значения xmin до максимального значения xmax.

Графические возможности пакета Mathematica
Для построения двумерных графиков функций вида f(x) используется встроенная в ядро функция Plot. Она задается в следующих формах:
Формат построенных графиков задается специальными графическими опциями и директивами.
С функцией Plot используются различные опции, меняющие те или иные параметры графиков и их вид (например, размер графика, наличие осей и т.д.) Опции внутри записей графических функций задаются своим именем name и значением value в виде: name-> value
Значениями опций могут быть числа, списки, логические утверждения True, False и специальные слова, например:
Automatic - используется автоматический выбор;
None - опция не используется;
All - используется в любом случае.

Поскольку графики являются объектами, то они могут быть значениями переменных. Поэтому Mathematica допускает следующие конструкции:
Plot[Sin[x],{x,0,20}] - построение графика синусоиды;
g:=Plot [Sin [x], {х, 0, 20} ] - задание объекта - графика синусоиды - с отложенным выводом;
g=Plot [Sin [x], {х, 0, 20} ] - задание объекта - графика синусоиды - с немедленным выводом.
Графические возможности пакета Mathematica

Графические возможности пакета Mathematica
Опции функции Plot
С функцией Plot используются различные опции, меняющие те или иные параметры графиков и их вид (например, размер графика, наличие осей и т.д.). Опции внутри записей графических функций задаются своим именем name и значением value в виде:
name -> value
Значениями опций могут быть числа, списки, логические утверждения True и False и специальные слова, например:
Autonomic – используется автоматический выбор;
None – опция не используется;
All – используется в любом случае;
True – используется;
False – не используется.

Графические возможности пакета Mathematica
Ниже представлены основные опции для графических функций (звездочкой отмечены те опции, которые можно использовать и в трехмерной графике):

Графические возможности пакета Mathematica
Опции могут серьезно изменить вид графика.
Примеры использования опций графики:
Установка масштаба 2D–графика по оси y
Plot[Sin[x]/x,{x,-20,20},PlotRange->{-0.25,1}]
Ввод надписей по осям 2D – графика
Plot[Sin[x]^3,{x,0,20},AxesLabel->{“x value”,”Graphic Sin(x)^3”}]
График с титульной надписью
Plot[Sin[x]^3,{x,0,20},Axes->None,PlotLabel->”Graphic for functions Sin(x)^3”]

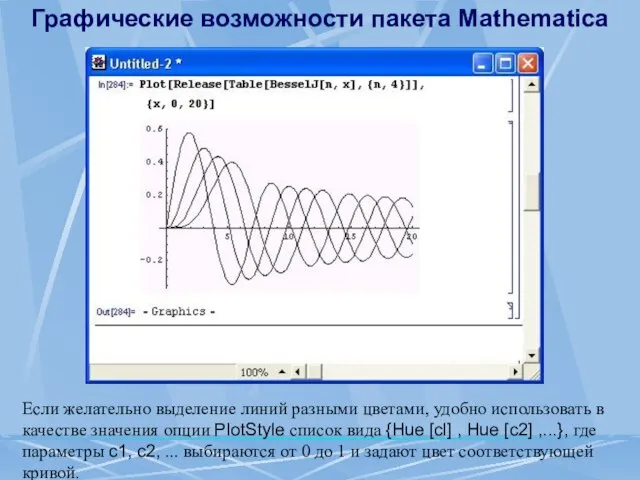
Графические возможности пакета Mathematica
Если желательно выделение линий разными цветами, удобно использовать в качестве значения опции PlotStyle список вида {Hue [cl] , Hue [с2] ,...}, где параметры c1, с2, ... выбираются от 0 до 1 и задают цвет соответствующей кривой.

Графические возможности пакета Mathematica
Директивы двумерной графики
Еще одним мощным средством графики системы являются графические директивы. Они указывают, с какими графическими параметрами (цвет, толщина линий, их стиль и т.д.) должна строить графики та или иная функция.
В системе используются следующие директивы двумерной графики:
Пример использования директив двумерной графики:
Plot[Sin[x],{x,0,20},PlotStyle-> Dashing[{0.05,0.025}]]

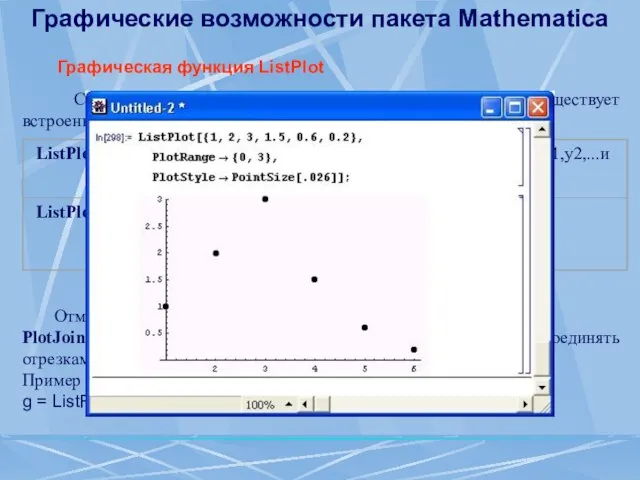
Графические возможности пакета Mathematica
Графическая функция ListPlot
Строить графики часто приходится по точкам. Для этого существует встроенная в ядро системы функция ListPlot.
Отметим опцию для данной функции:
PlotJoineed – указывает, следует ли точки, нанесенные на график, соединять отрезками прямых (по умолчанию – True).
Пример использования функции ListPlot:
g = ListPlot[{1,2,3,1.5,0.5,0.2},PlotRange->{0,3}]

Получение информации о графических объектах
Информацию об опциях графического объекта g дают следующие функции:
FullAxes [g] — возвращает список опций координатных осей;
Options [g] - возвращает упрощенный список опций;
FullOptions [g] - возвращает полный список опций;
InputForm[g] - возвращает информацию о графике (включая таблицу точек).
Пусть задан графический объект g: g:=Plot[Sin[x],{х,-10,10}]
Ниже представлено получение упрощенного списка опций этого графического объекта:
Options[g]
{PlotRange -> Automatic, AspectRatio ->1/GoldenRatio,
DisplayFunction :> $DisplayFunction, ColorOutput -> Automatic, Axes -> Automatic, AxesOrigin -> Automatic, PlotLabel -> None, AxesLabel -> None, Ticks -> Automatic, GridLines -> None, Prolog -> {}, Epilog -> {}, AxesStyle -> Automatic, Background -> Automatic, DefaultColor -> Automatic, DefaultFont :> $DefaultFont, RotateLabel -> True, Frame -> False, FrameStyle -> Automatic, FrameTicks -> Automatic!, FrameLabel -> None, PlotRegion -> Automatic, ImageSize -> Automatic, TextStyle :> $TextStyle, FormatType :> $FormatType}
Графические возможности пакета Mathematica

Графические возможности пакета Mathematica
Перестройка и комбинирование графиков
При построении графиков приходится изменять их вид, а также те или иные параметры и опции. Для этого можно повторить вычисления, но тогда заметно снизится скорость работы с системой. Для ее повышения удобно использовать специальные функции перестройки и вывода графиков, учитывающих что узловые точки этих графиков уже были рассчитаны и их координаты хранятся в памяти ПК.
В этом случае удобно использовать следующие функции:
Примеры: Построение объединенного сдвоенного 2D-графика
g1 = Plot[Sin[x],{x,0,20}];
g2 = Plot[Sin[x]^3,{x,0,20}];
Show[g1,g2,PlotRange->{-1.5,1.5}]

Графические возможности пакета Mathematica
Примитивы двумерной графики
Примитивами двумерной графики называют дополнительные указания, вводимые в функцию Graphics, для построения с ее помощью некоторых геометрических фигур. Сама функция Graphics задается в следующем виде:
Graphics[primitives,options]
Применение примитивов в составе функции Graphics избавляет пользователя от задания довольно сложных математических выражений, описывающих эти фигуры, и описания алгоритмов построения по ним графиков фигур. Примитивы могут дополнять и иные функции.

Графические возможности пакета Mathematica

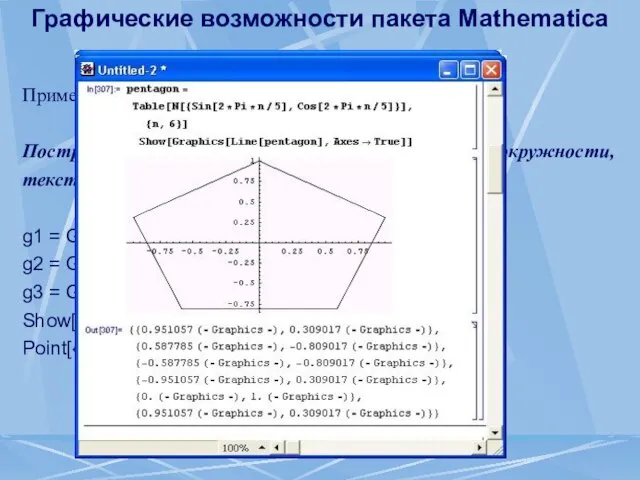
Графические возможности пакета Mathematica
Примеры использования примитивов двумерной графики:
Построение четырех графических объектов – линии, окружности, текста и жирной точки.
g1 = Graphics[Line[{{-1,-1},{1,1}}]];
g2 = Graphics[Circle[{0,0},0.8}};
g3 = Graphics[Text[“Привет!”{0.25,0.5}]];
Show[g1,g2,g3,Graphics[{PointSize[0.032],
Point[{-0.5,0.2}]],Axes->Autonomic]

Графические возможности пакета Mathematica
Построение графиков параметрически заданных функций
Функции, графики которых строятся на плоскости, могут быть заданы в параметрическом виде: x=fx(t) и y=fy(t), где независимая переменная t меняется от минимального значения tmin до максимального tmax с шагом dt. Особенно удобно применение таких функций для построения замкнутых линий, таких как окружности, эллипсы, циклоиды и др.
Для построения параметрически заданных функций используются следующие графические функции системы:

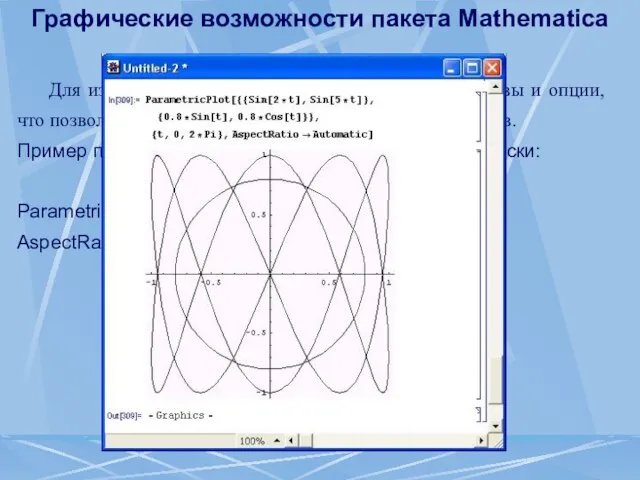
Графические возможности пакета Mathematica
Для изменения вида графиков используются директивы и опции, что позволяет реализовать большое разнообразие графиков.
Пример построения графика, заданного параметрически:
ParametricPlot[{Sin[2*t],Sin[3*t]},{t,0,2Pi},
AspectRatio->Automatic]

Графические возможности пакета Mathematica
Построение графиков трехмерных поверхностей.
Функция двух переменных z = f(x,y) в пространстве образует некоторую трехмерную поверхность или фигуру. Для их построения приходится использовать координатную систему с тремя осями координат: x, y, z.
Для построения графиков трехмерных поверхностей используются следующие основные графические функции:

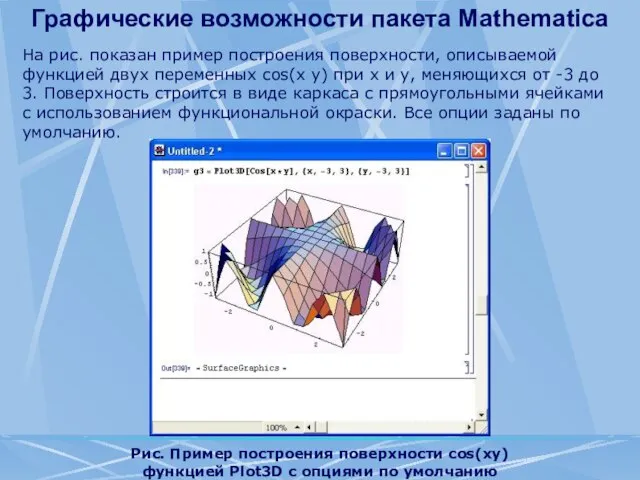
Графические возможности пакета Mathematica
Рис. Пример построения поверхности cos(xy)
функцией Plot3D с опциями по умолчанию
На рис. показан пример построения поверхности, описываемой функцией двух переменных cos(x у) при х и у, меняющихся от -3 до 3. Поверхность строится в виде каркаса с прямоугольными ячейками с использованием функциональной окраски. Все опции заданы по умолчанию.

Графические возможности пакета Mathematica
Опции и директивы трехмерной графики
Для модификации трехмерных графиков могут использоваться многочисленные опции и директивы.

Графические возможности пакета Mathematica
Для построения трехмерных графиков в параметрической форме также имеются функции:
Примеры построения трехмерных графиков:
Исходная математическая поверхность
g3=Plot3D[Cos[x*y],{x,-3,3},{y,-3,3},PlotPoints->40]
Математическая поверхность с отсеченной верхней частью
Show[g3,PlotRange->{0,0.5}]

Графические возможности пакета Mathematica
Примитивы трехмерной графики
Наряду с построением графиков поверхностей, заданных аналитическими выражениями, имеется возможность создания графиков различных объектов с помощью функции
Graphics3D[primitives,options] - представляет трехмерное графическое изображение.
Основные примитивы:

Графические возможности пакета Mathematica
Примеры:
Построение куба с точками
pts=Table[Point[{Random[],Random[],Random[]}],{25}];
Show[Graphics3D[{PointSize[0.014],pts}]]
Show[Graphics3D[pts],ViewPoint->{8,2,2}]
Построение шести кубов в пространстве
g=Graphics3D[{Cuboid[{0,0,0}],Cuboid[{2,2,2}], Cuboid[{0,1,2}], Cuboid[{1,1,3}],Cuboid[{3,2,1}],
Cuboid[{2,1,1}],Cuboid[{3,3,3}]}];
Show[g]

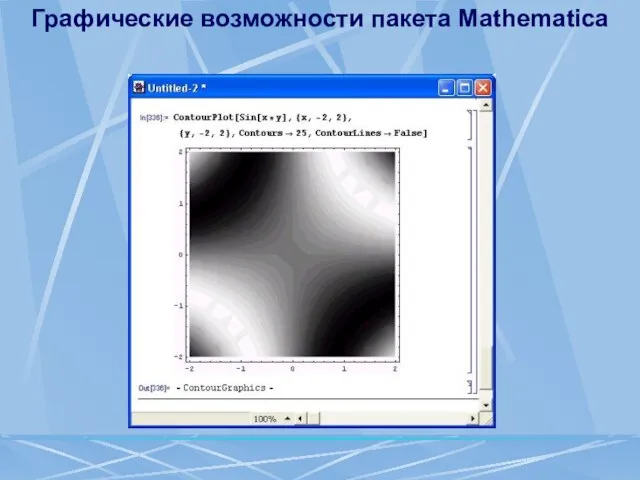
Графические возможности пакета Mathematica
Построение контурных графиков
Контурные графики, или графики линий равных высот, используются для отображения поверхностей на плоскости. Они удобны для выявления всех экстремумов функций в пределах области графика. Такие графики являются линиями пересечения поверхности с секущими горизонтальными плоскостями, расположенными параллельно друг под другом. Они часто используются в картографии.
Основными функциями и директивами для построения контурных графиков являются следующие:
ContourPlot[f,{x, xmin, xmax}, {у, ymin, ymax}] — порождает контурный график f как функции от х и у;
ContourGraphics [array] — представляет контурный график массива array;
ListContourPlot[array] — формирует контурный график из массива величин высот.

Графические возможности пакета Mathematica
Для управления возможностями графической функции ContourPlot используются опции, полный список которых выводит команда Options [ContourGraphics ]. Помимо уже рассмотренных ранее опций используются следующие:
ColorFunction — задает окраску областей между линиями;
Contours — задает число контурных линий;
ContourLines — задает прорисовку явных (explicit) контурных линий;
ContourShading — задает затенение областей между контурными линиями;
ContourSmoothing — задает сглаживание контурных линий;
ContourStyle — задает стиль рисуемых линий для контурных графиков;
MeshRange — задает области изменения х- и y-координат.

Графические возможности пакета Mathematica

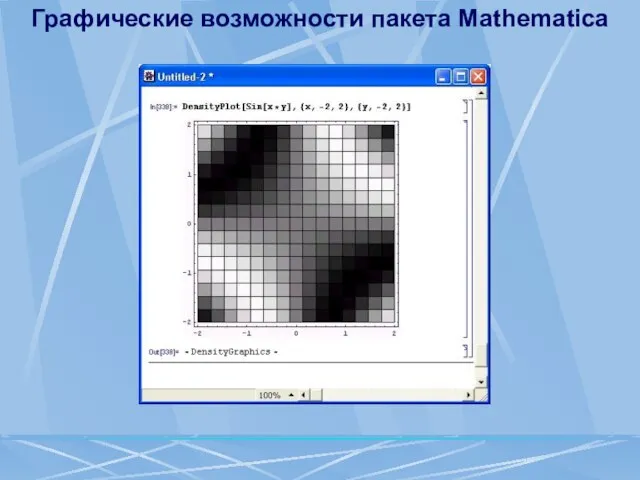
Графические возможности пакета Mathematica
Построение графиков плотности
Функцией двух переменных f(x, у) может описываться плотность некоторой среды. Для построения графиков плотности используются следующие графические функции:
DensityGraphics [array] — является представлением графика плотности;
DensityPlot[f, {х, xmin, xmax}, {у, ymin, ymax}] — строит график плотности f как функции от х и у;
ListDensityPlot [array] — формирует график плотности из массива величин высот.

Графические возможности пакета Mathematica

Лекция окончена
Нажмите клавишу
для выхода

Графические возможности пакета Mathematica
Графика всегда была козырной картой системы. Графические возможности достигаются как обилием встроенных функций, так и средствами их модификации с помощью директив, опций и примитивов. Система позволяет строить практически любые виды математических графиков, причем обычного пользователя в большинстве случаев удовлетворяют графики, параметры которых система задает по умолчанию.
Начнем рассмотрение графических возможностей системы с построения графиков функций одной переменной вида y = f(x) или просто f(x). График таких функций строится на плоскости, т.е. в двумерном пространстве. Он представляет собой геометрическое место точек (y,x) при изменении независимой переменной х (абциссы) в заданных пределах, например от минимального значения xmin до максимального значения xmax.

Графические возможности пакета Mathematica
Для построения двумерных графиков функций вида f(x) используется встроенная в ядро функция Plot. Она задается в следующих формах:
Формат построенных графиков задается специальными графическими опциями и директивами.
С функцией Plot используются различные опции, меняющие те или иные параметры графиков и их вид (например, размер графика, наличие осей и т.д.) Опции внутри записей графических функций задаются своим именем name и значением value в виде: name-> value
Значениями опций могут быть числа, списки, логические утверждения True, False и специальные слова, например:
Automatic - используется автоматический выбор;
None - опция не используется;
All - используется в любом случае.

Графические возможности пакета Mathematica
Опции функции Plot
С функцией Plot используются различные опции, меняющие те или иные параметры графиков и их вид (например, размер графика, наличие осей и т.д.). Опции внутри записей графических функций задаются своим именем name и значением value в виде:
name -> value
Значениями опций могут быть числа, списки, логические утверждения True и False и специальные слова, например:
Autonomic – используется автоматический выбор;
None – опция не используется;
All – используется в любом случае.

Графические возможности пакета Mathematica
Ниже представлены основные опции для графических функций (звездочкой отмечены те опции, которые можно использовать и в трехмерной графике):

Графические возможности пакета Mathematica
Опции могут серьезно изменить вид графика.
Примеры использования опций графики:
Установка масштаба 2D–графика по оси y
Plot[Sin[x]/x,{x,-20,20},PlotRange->{-0.25,1}]
Ввод надписей по осям 2D – графика
Plot[Sin[x]^3,{x,0,20},AxesLabel->{“x value”,”Graphic Sin(x)^3”}]
График с титульной надписью
Plot[Sin[x]^3,{x,0,20},Axes->None,PlotLabel->”Graphic for functions Sin(x)^3”]

Графические возможности пакета Mathematica
Директивы двумерной графики
Еще одним мощным средством графики системы являются графические директивы. Они указывают, с какими графическими параметрами (цвет, толщина линий, их стиль и т.д.) должна строить графики та или иная функция.
В системе используются следующие директивы двумерной графики:
Пример использования директив двумерной графики:
Plot[Sin[x],{x,0,20},PlotStyle-> Dashing[{0.05,0.025}]]

Графические возможности пакета Mathematica
Графическая функция ListPlot
Строить графики часто приходится по точкам. Для этого существует встроенная в ядро системы функция ListPlot.
Отметим опцию для данной функции:
PlotJoineed – указывает, следует ли точки, нанесенные на график, соединять отрезками прямых (по умолчанию – True).
Пример использования функции ListPlot:
g = ListPlot[{1,2,3,1.5,0.5,0.2},PlotRange->{0,3}]

Графические возможности пакета Mathematica
Перестройка и комбинирование графиков
При построении графиков приходится изменять их вид, а также те или иные параметры и опции. Для этого можно повторить вычисления, но тогда заметно снизится скорость работы с системой. Для ее повышения удобно использовать специальные функции перестройки и вывода графиков, учитывающих что узловые точки этих графиков уже были рассчитаны и их координаты хранятся в памяти ПК.
В этом случае удобно использовать следующие функции:
Примеры: Построение объединенного сдвоенного 2D-графика
g1 = Plot[Sin[x],{x,0,20}];
g2 = Plot[Sin[x]^3,{x,0,20}];
Show[g1,g2,PlotRange->{-1.5,1.5}]

Графические возможности пакета Mathematica
Примитивы двумерной графики
Примитивами двумерной графики называют дополнительные указания, вводимые в функцию Graphics, для построения с ее помощью некоторых геометрических фигур. Сама функция Graphics задается в следующем виде:
Graphics[primitives,options]
Применение примитивов в составе функции Graphics избавляет пользователя от задания довольно сложных математических выражений, описывающих эти фигуры, и описания алгоритмов построения по ним графиков фигур. Примитивы могут дополнять и иные функции.

Графические возможности пакета Mathematica

Графические возможности пакета Mathematica
Примеры использования примитивов двумерной графики:
Построение четырех графических объектов – линии, окружности, текста и жирной точки.
g1 = Graphics[Line[{{-1,-1},{1,1}}]];
g2 = Graphics[Circle[{0,0},0.8}};
g3 = Graphics[Text[“Hello!”{0.25,0.5}]];
Show[g1,g2,g3,Graphics[{PointSize[0.032],
Point[{-0.5,0.2},Axes->Autonomic]

Графические возможности пакета Mathematica
Построение графиков параметрически заданных функций
Функции, графики которых строятся на плоскости, могут быть заданы в параметрическом виде: x=fx(t) и y=fy(t), где независимая переменная t меняется от минимального значения tmin до максимального tmax с шагом dt. Особенно удобно применение таких функций для построения замкнутых линий, таких как окружности, эллипсы, циклоиды и др.
Для построения параметрически заданных функций используются следующие графические функции системы:

Графические возможности пакета Mathematica
Для изменения вида графиков используются директивы и опции, что позволяет реализовать большое разнообразие графиков.
Пример построения графика, заданного параметрически:
ParametricPlot[{Sin[2*t],Sin[3*t]},{t,0,2Pi},
AspectRatio->Automatic]

Графические возможности пакета Mathematica
Построение графиков трехмерных поверхностей.
Функция двух переменных z = f(x,y) в пространстве образует некоторую трехмерную поверхность или фигуру. Для их построения приходится использовать координатную систему с тремя осями координат: x, y, z.
Для построения графиков трехмерных поверхностей используются следующие основные графические функции:

Графические возможности пакета Mathematica
Для построения трехмерных графиков в параметрической форме также имеются функции:
Примеры построения трехмерных графиков:
Исходная математическая поверхность
g3=plot3D[Cos[x*y],{x,-3,3},{y,-3,3},PlotPoints->40]
Математическая поверхность с отсеченной верхней частью
Show[g3,PlotRange->{0,0.5}]

Графические возможности пакета Mathematica
Примитивы трехмерной графики
Наряду с построением графиков поверхностей, заданных аналитическими выражениями, имеется возможность создания графиков различных объектов с помощью функции
Graphics3D[primitives,options] - представляет трехмерное графическое изображение.
Основные примитивы:

Графические возможности пакета Mathematica
Примеры:
Построение куба с точками
pts=Table[Point[{Random[],Random[],Random[]}],{25}];
Show[Graphics3D[{PointSize[0.014],pts}]]
Show[Graphics3D[pts],ViewPoint->{8,2,2}]
Построение шести кубов в пространстве
g=Graphics3D[{Cuboid[{0,0,0}],Cuboid[{2,2,2}],
Cuboid[{1,1,3}],Cuboid[{3,2,1}], Cuboid[{2,1,1}],Cuboid[{3,3,3}]}];
Show[g]