Тема: Применение теории графов в программировании

Гипотеза
Теория графов подходит для решения транспортных задач
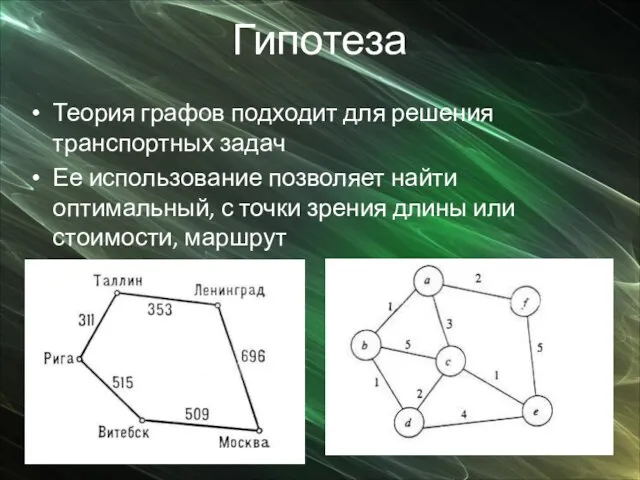
Ее использование позволяет найти оптимальный, с точки зрения длины или стоимости, маршрут

Теория графов
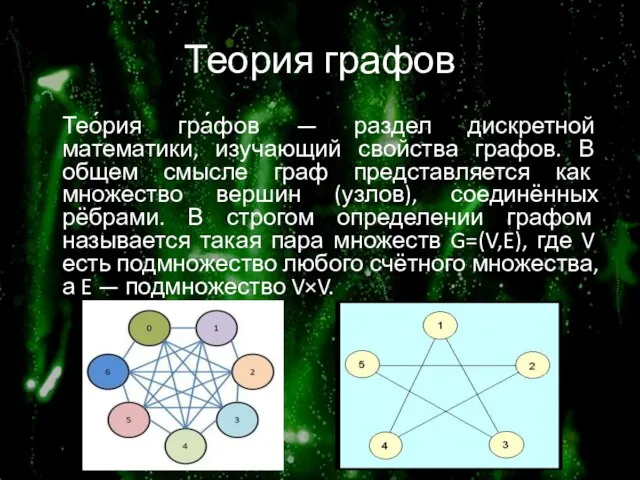
Тео́рия гра́фов — раздел дискретной математики, изучающий свойства графов. В общем смысле граф представляется как множество вершин (узлов), соединённых рёбрами. В строгом определении графом называется такая пара множеств G=(V,E), где V есть подмножество любого счётного множества, а E — подмножество V×V.

Задача коммивояжера
Коммивояжер (бродячий торговец) должен выйти из первого города и, посетив по разу в неизвестном порядке города 2,3,...n, вернуться обратно в первый город. В каком порядке надо обходить города, чтобы замкнутый путь (тур) коммивояжера был кратчайшим?

Главная функция и инициализация глобальных переменных
int Pmin[N], // лучшая перестановка
P[N], // текущая перестановка
Lmin, // минимальная длина
L, // текущая длина
D[N][N]; // матрица расстояний
void main()
{
Lmin = 32767; // большое число
L = 0;
P[0] = 1; // начальная вершина 1
Commi(1); // построить тур
for ( int i = 0; i < N; i ++ ) // вывести результат
printf("%d ", Pmin[i]);
}

Метод «грубой силы»
void Commi( int q ) // q – число уже поставленных вершин
{
int i, temp;
if ( q == N ) { // перестановка получена
if ( L < Lmin ) {
Lmin = L;
for ( i = 0; i < N; i ++ ) // запомнить новый минимальный тур
Pmin[i] = P[i];
}
return;
}
for ( i = q; i < N; i ++ ) {
temp = P[q]; P[q] = P[i]; P[i] = temp; // P[q] <-> P[i]
L += D [P[q-1]] [P[q]]; // добавить ребро
Commi ( q+1 ); // рекурсивный вызов
L -= D [P[q-1]] [P[q]]; // убрать ребро
temp = P[q]; P[q] = P[i]; P[i] = temp; // P[q] <-> P[i]
}
}

Метод ветвей и границ
void Commi( int q ) // q – число уже поставленных вершин
{
int i, temp;
if ( q == N ) { // перестановка получена
if ( L < Lmin ) {
Lmin = L;
for ( i = 0; i < N; i ++ ) // запомнить новый минимальный тур
Pmin[i] = P[i];
}
return;
}
for ( i = q; i < N; i ++ ) {
temp = P[q]; P[q] = P[i]; P[i] = temp;
L += D [P[q-1]] [P[q]];
if ( L < Lmin ) Commi ( q+1 );
L -= D [P[q-1]] [P[q]];
temp = P[q]; P[q] = P[i]; P[i] = temp;
}
}

Метод случайных перестановок
Используют метод случайных перестановок. В алгоритме повторяются следующие шаги:
1. Выбрать случайным образом номера вершин i и j в перестановке.
2. Если при перестановке вершин с номерами i и j длина пути уменьшилась, такая перестановка принимается.

Использование теории графов в других сферах
В химии;
В информатике и программировании
В коммуникационных и транспортных системах
В экономике
В логистике
В схемотехнике

Дополнительные материалы
Графы как waypoints: AVIГрафы как waypoints: AVI MPG

Заключение
Графы находят широкое применение в различных сферах жизни;
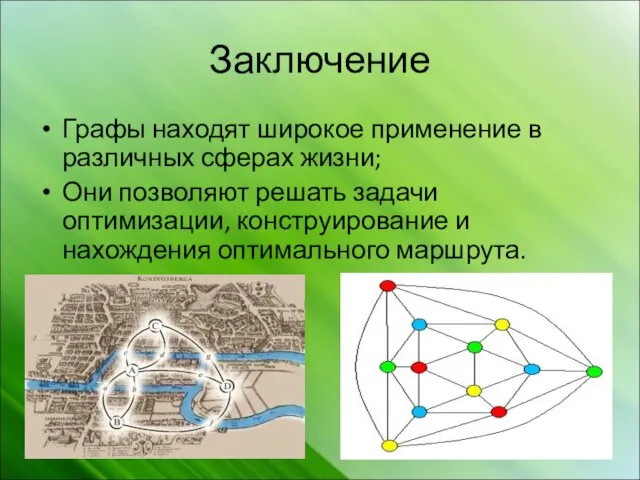
Они позволяют решать задачи оптимизации, конструирование и нахождения оптимального маршрута.

Промо – ролик
Avi version.
Mpg version.