Теорема Пифагора

Упоминания о теореме
Пифагора
Витрувий
(Римский архитектор и инженер)
Плутарх
(Греческий пистель и моралист I в.)
Диоген
(Греческий ученый III в.)
Прокл
(математик V в.)

Родина ученого
о. Самос (Греция)

Жизненный путь Пифагора
Греция
(о. Самос)
Египет
Вавилон
Греция
(о. Самос)
Южная Италия
(г. Кротон)

Заповеди Пифагора, как учителя философии
Мысль – превыше всего между людьми на земле.
Не садись на хлебную меру (не живи праздно).
Уходя, не оглядывайся (перед смертью не цепляйся за жизнь).
По торной дороге не ходи (следуй не мнениям толпы, а мнениям немногих понимающих).
Будь с тем, кто ношу взваливает, не будь с тем, кто ношу сваливает (поощряй людей не к праздности, а к добродетели и труду).

Формулировки теоремы
Формулировка Евклида:
В прямоугольном треугольнике квадрат стороны, натянутый над прямым углом, равен квадратам на сторонах, заключающих прямой угол.
В Geometria Culmonensis
теорема читается так:
Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как и у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу.

Древнекитайское доказательство
b a
b
a
a b
a
b

Чертеж из трактата «Чжоу-би»

Доказательство Евклида
A
B
C
F
H
D
E
G
K
L
J

Алгебраическое доказательство
α+β= 90°
α+β+γ=180°
γ=90°
S(Q)=S(P)+4S(T) .
S(Q)=(a+b)2; S(P)=c2 и S(T)=1/2(ab)
(a+b) 2=c2+4·(1/2)ab
a2+b2+2ab=c2+2ab
с2=а2+b2

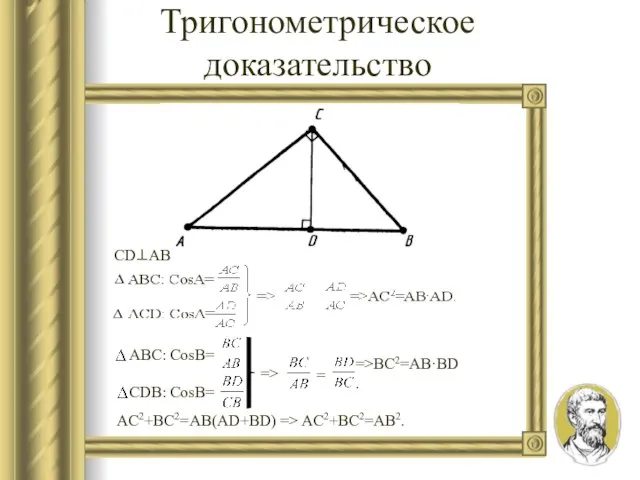
Тригонометрическое доказательство
CD⊥AB
AC2+BC2=AB(AD+BD) => AC2+BC2=AB2.

Векторное доказательство
А
С
В
a = 90°, cos90° = 0
AB2=AC2+BC2

Пифагоровы числа

Задача
∠A = ∠D = 45°
4 м
AK = DK = a, BK = CK = b.
DB2 = DK2 + KB2 = a2 + b2 = 16.

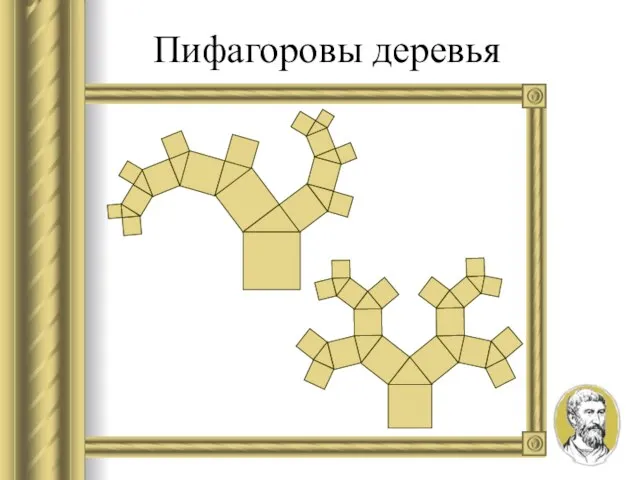
Пифагоровы деревья