Слайд 2Цели урока:
Ввести определение средней линии треугольника.
Сформулировать и доказать теорему о средней линии

треугольника.
Рассмотреть решение задач на применение доказанной теоремы.
Рассмотреть решение задачи о свойстве медиан треугольника.
Слайд 3Ход урока
Решение задач по готовым чертежам.
Изучение нового материала.
Закрепление изученной темы.
Итоги урока
Домашнее задание

Слайд 4Решение задач
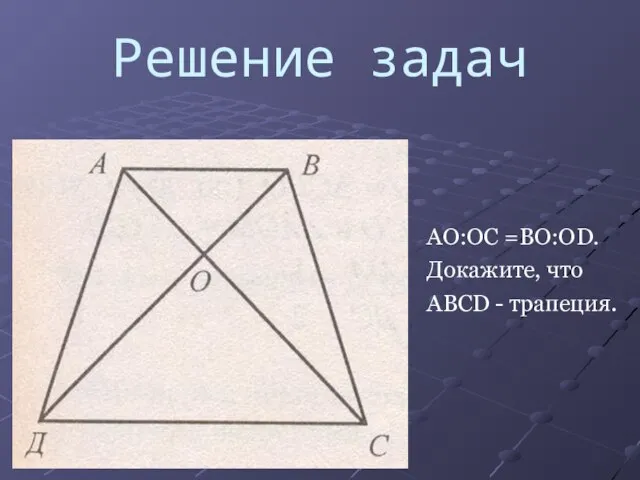
AO:OC =BO:OD.
Докажите, что
ABCD - трапеция.
Слайд 5Решение задач
По второму
признаку подобия
треугольников
ABO подобен COD,
Поэтому угол
BAO = углу OCD,
тогда AB
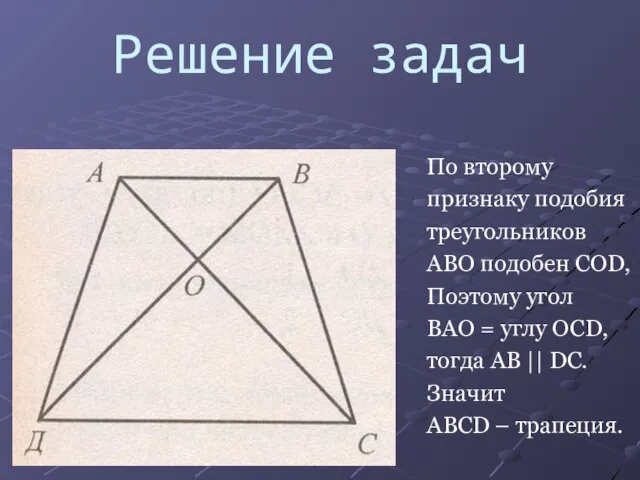
|| DС.
Значит
ABCD – трапеция.
Слайд 6Решение задач
М и N – середины сторон AB и BC. Докажите, что
MN
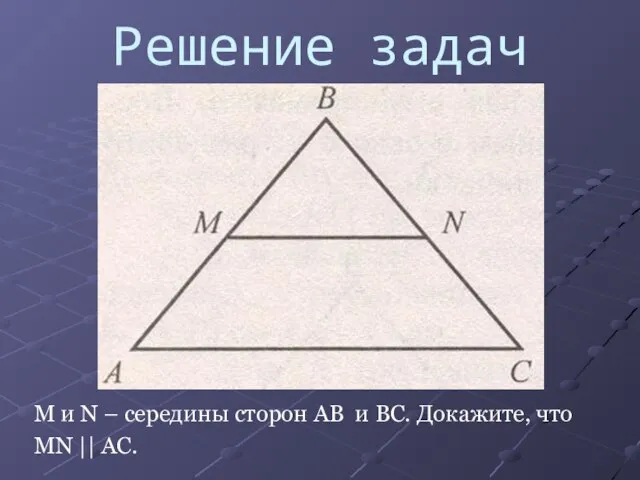
|| AC.
Слайд 7Решение задач
По второму признаку подобия треугольников ABC
подобен MBN, поэтому угол BMN =
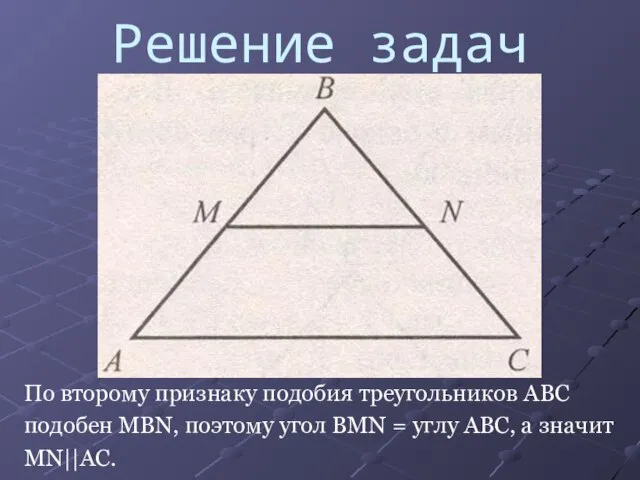
углу ABC, а значит
MN||AC.
Слайд 8Объяснение нового материала
Определение средней линии треугольника.
Теорема о средней линии треугольника.

Слайд 9Закрепление изученного материала
№ 564 (устно)
№ 567
№ 1
№ 570

Слайд 10Решение задачи № 567
MN – средняя линия ABD
MN||DB и MN = ½
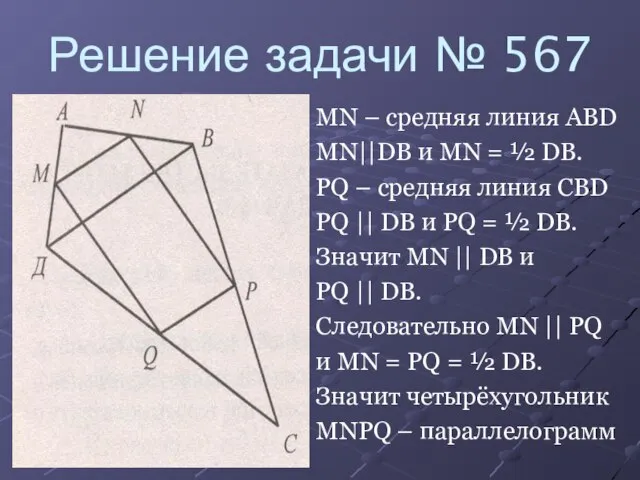
DB.
PQ – средняя линия CBD
PQ || DB и PQ = ½ DB.
Значит MN || DB и
PQ || DB.
Следовательно MN || PQ
и MN = PQ = ½ DB.
Значит четырёхугольник
MNPQ – параллелограмм
Слайд 11Решение задачи № 570
Треугольник AMO подобен треугольнику CDO по двум
углам (MAO =
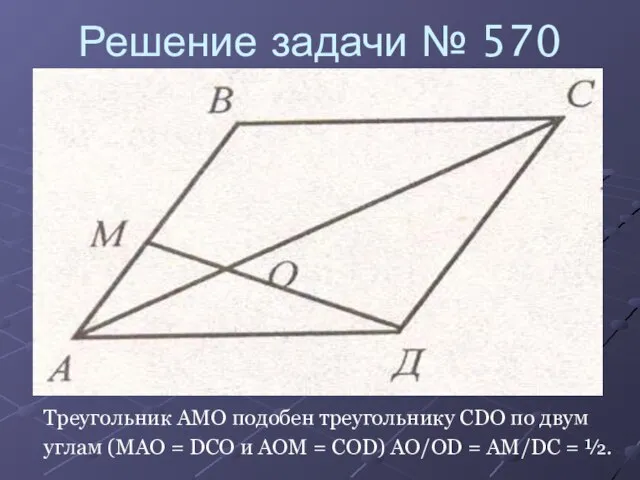
DCO и AOM = COD) AO/OD = AM/DC = ½.
Слайд 12Итог урока
Если AM = MB и MN = NC, то MN ||
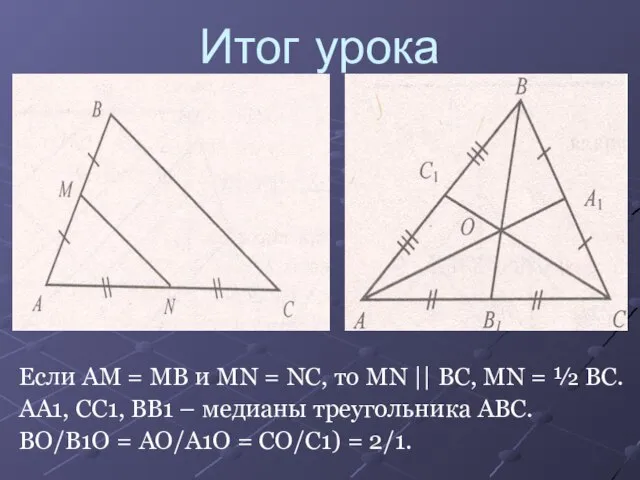
BC, MN = ½ BC.
AA1, CC1, BB1 – медианы треугольника ABC.
BO/B1O = AO/A1O = CO/C1) = 2/1.
Слайд 13Домашнее задание
Вопросы стр. 154: 8, 9.
№ 565
№ 566
№ 571













 Номинант в категории эталонная работа. Служба закупок
Номинант в категории эталонная работа. Служба закупок Светочи Земли Кривополянской
Светочи Земли Кривополянской Сюткин Виктор Михайлович Заместитель генерального директора по научной работе ООО Научно-производственный центр экологического
Сюткин Виктор Михайлович Заместитель генерального директора по научной работе ООО Научно-производственный центр экологического Экономические системы
Экономические системы Презентация на тему таблица умножения
Презентация на тему таблица умножения  Развитие малого и среднего предпринимательства в России
Развитие малого и среднего предпринимательства в России Драг-рейсинг — гоночное соревнование
Драг-рейсинг — гоночное соревнование Whether the management consultancy could be considered a profession or not
Whether the management consultancy could be considered a profession or not Мистический 2012 год. Планета Нибиру
Мистический 2012 год. Планета Нибиру Школа испанского языка CENTRO PICASSO. Пословицы в испанском и русском языках
Школа испанского языка CENTRO PICASSO. Пословицы в испанском и русском языках Волшебные нотки
Волшебные нотки Способ плоско параллельного перемещения
Способ плоско параллельного перемещения § 42. Барометр-анероид
§ 42. Барометр-анероид Использование блоков при создании чертежа
Использование блоков при создании чертежа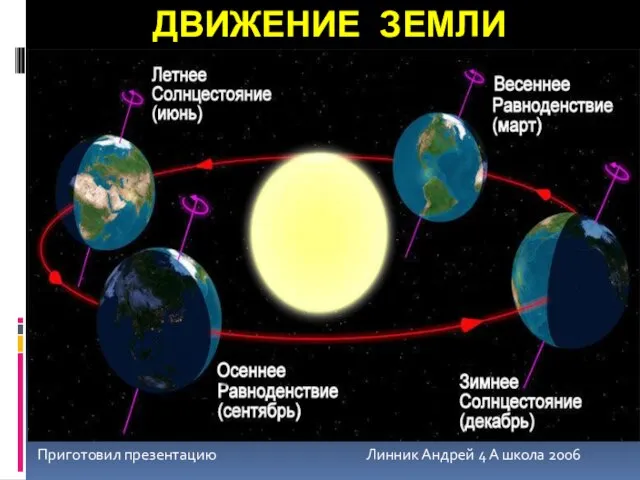 Движение Земли (4 класс)
Движение Земли (4 класс) По страницам Красной книги
По страницам Красной книги Click to edit Master title style Click to edit Master subtitle style
Click to edit Master title style Click to edit Master subtitle style  учитель английского языка МОУ Прогимназия №1 Шашкова Лилия Владимировна г. Электрогорск Ул. Советская д. 5 кв. 72. Тел. 3-47-49 2008 год
учитель английского языка МОУ Прогимназия №1 Шашкова Лилия Владимировна г. Электрогорск Ул. Советская д. 5 кв. 72. Тел. 3-47-49 2008 год Автоматизация продаж полисов в удаленных и партнерских точках, мобильные технологии снижения рисков
Автоматизация продаж полисов в удаленных и партнерских точках, мобильные технологии снижения рисков Интегрированный урок физики и биологии
Интегрированный урок физики и биологии Современные технологии и материалы для садово-паркового и ландшафтного строительства
Современные технологии и материалы для садово-паркового и ландшафтного строительства Презентация на тему движение воды в океане 6 класс
Презентация на тему движение воды в океане 6 класс English pronouns
English pronouns  Массовая культура и повседневная жизнь. Горожане и фермеры
Массовая культура и повседневная жизнь. Горожане и фермеры Объем конуса
Объем конуса Plants and Arthropods Friends or Foes
Plants and Arthropods Friends or Foes Быстрый путьот стартапа до бизнеса
Быстрый путьот стартапа до бизнеса Страна городов
Страна городов