Слайд 2ОБЛАСТИ ПРИМЕНЕНИЯ
Строительство
Астрономия
Мобильная связь

Слайд 3Мобильная связь
Какую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно

было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.)
Решение:
Пусть AB= x, BC=R=200 км, OC= r =6380 км.
OB=OA+AB
OB=r + x.
Используя теорему Пифагора, получим Ответ: 2,3 км.
Слайд 4Строительство
Окна
Крыши
Молниеотводы

Слайд 5Молниеотвод
Известно, что молниеотвод защищает от молнии все предметы, расстояние которых от его

основания не превышает его удвоенной высоты. Необходимо определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.
Решение:
По теореме Пифагора h2≥ a2+b2, значит h≥(a2+b2)1/2.
Слайд 6Окна
В зданиях готического и романского стиля верхние части окон расчленяются каменными ребрами,

которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны
ширине окна (b) для наружных дуг
половине ширины, (b/2) для внутренних дуг
Остается еще полная окружность, касающаяся четырех дуг. Т. к. она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между
этими окружностями, т. е. b/2 и, следовательно,
радиус равен b/4. А тогда становится ясным и
положение ее центра.
Слайд 7В романской архитектуре часто встречается мотив, представленный на рисунке. Если b по-прежнему

обозначает ширину окна, то радиусы полуокружностей будут равны R = b / 2 и r = b / 4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+p, один катет равен b/4, а другой b/2-p. По теореме Пифагора имеем:
(b/4+p)=( b/4)+( b/4-p)
или
b/16+ bp/2+p=b/16+b/4-bp+p,
откуда
bp/2=b/4-bp.
Разделив на b и приводя подобные члены, получим:
(3/2)p=b/4, p=b/6.
Слайд 8Астрономия
На этом рисунке показаны точки A и B и путь светового луча
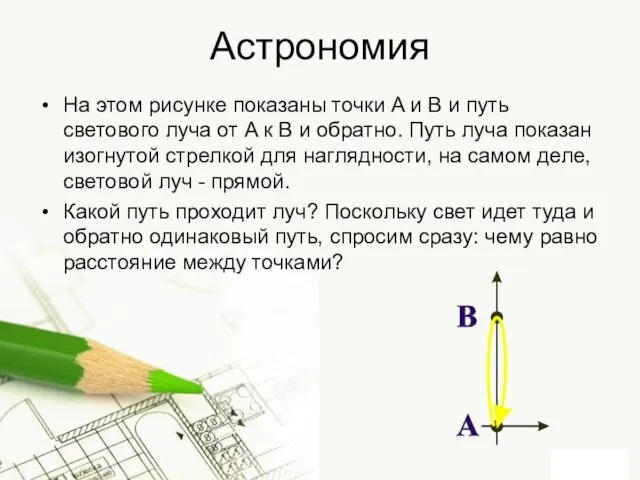
от A к B и обратно. Путь луча показан изогнутой стрелкой для наглядности, на самом деле, световой луч - прямой.
Какой путь проходит луч? Поскольку свет идет туда и обратно одинаковый путь, спросим сразу: чему равно расстояние между точками?
Слайд 9На этом рисунке показан путь светового луча только с другой точки зрения,
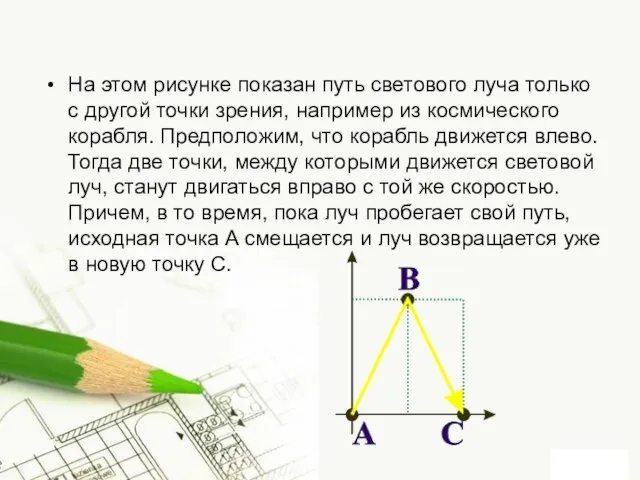
например из космического корабля. Предположим, что корабль движется влево. Тогда две точки, между которыми движется световой луч, станут двигаться вправо с той же скоростью. Причем, в то время, пока луч пробегает свой путь, исходная точка A смещается и луч возвращается уже в новую точку C.
Слайд 10В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных

человеку. В шутку, хотя и не совсем безосновательно , было решено передать обитателям Марса сигнал в виде теоремы Пифагора. Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.
Слайд 11Строительство крыши
При строительстве домов и коттеджей часто встает вопрос о длине

стропил для крыши, если уже изготовлены балки. Например: в доме задумано построить двускатную крышу (форма в сечении). Какой длины должны быть стропила, если изготовлены балки AC=8 м., и AB=BF.
Решение:
Треугольник ADC - равнобедренный AB=BC=4 м., BF=4 м. Если предположить, что FD=1,5 м., тогда:
А) Из треугольника DBC: DB=2,5 м.,
Б) Из треугольника ABF:










 Презентация на тему Что мы знаем о тексте 5 класс
Презентация на тему Что мы знаем о тексте 5 класс день учителя
день учителя Картины Рафаэля
Картины Рафаэля Организация процесса приготовления и приготовление блюд национальной и зарубежной кухни. Практика
Организация процесса приготовления и приготовление блюд национальной и зарубежной кухни. Практика Классификация документов
Классификация документов Baroque
Baroque Административное право как отрасль права
Административное право как отрасль права Пифагор. За легендой - Истина
Пифагор. За легендой - Истина Речные террасы. Река Барнёва.
Речные террасы. Река Барнёва. Час Океана
Час Океана Демонстрационный материал для практического занятия по теме: КИНЕМАТИКА Разработал: к.т.н., доцент Б.И. Генкин
Демонстрационный материал для практического занятия по теме: КИНЕМАТИКА Разработал: к.т.н., доцент Б.И. Генкин МультиТредовые архитектуры
МультиТредовые архитектуры Социальные права человека
Социальные права человека Лето в ЦМИТ Генезис
Лето в ЦМИТ Генезис Презентация на тему Ордена Великой Отечественной войны
Презентация на тему Ордена Великой Отечественной войны  КОНКУРС ПЕДАГОГИЧЕСКОГО МАСТЕРСТВА
КОНКУРС ПЕДАГОГИЧЕСКОГО МАСТЕРСТВА Мосты в искусстве
Мосты в искусстве Военно-образовательные учреждения РФ
Военно-образовательные учреждения РФ Дебальцевская общеобразовательная школа І-ІІІст. №3 Химия в загадках Подготовила ученица 11-А класса
Дебальцевская общеобразовательная школа І-ІІІст. №3 Химия в загадках Подготовила ученица 11-А класса Тестирование продуктаБаринов Дмитрий
Тестирование продуктаБаринов Дмитрий Ориентирование на местности
Ориентирование на местности Скажи жизни: «Да!»
Скажи жизни: «Да!»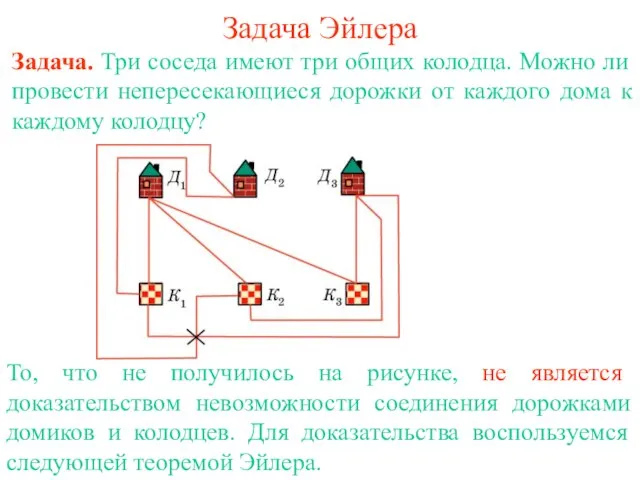 Задача Эйлера
Задача Эйлера Проект: «Лесенка успеха».
Проект: «Лесенка успеха». Нобелевские лауреаты 2010 года
Нобелевские лауреаты 2010 года Презентация на тему Строение цветка
Презентация на тему Строение цветка  ПНП_1
ПНП_1 Презентация на тему Качественные и количественные рынка гражданской авиации
Презентация на тему Качественные и количественные рынка гражданской авиации