Содержание
- 2. Основные понятия Механизмами называют изолированную часть некоторой механической системы (без источников и потребителей энергии), предназначенную для
- 3. Лихтенхельдт В. Синтез механизмов. – М.: Наука, 1978. – 228 с. «Вопрос о том, какие механизмы
- 4. Звенья шарнирно-рычажных механизмов Стойка – неподвижное звено механизма, на котором закреплены все другие его звенья. Кривошип
- 5. Различные варианты определения «кулисы» Кулиса – звено, вращающееся относительно подвижной оси (с направляющими для ползуна -
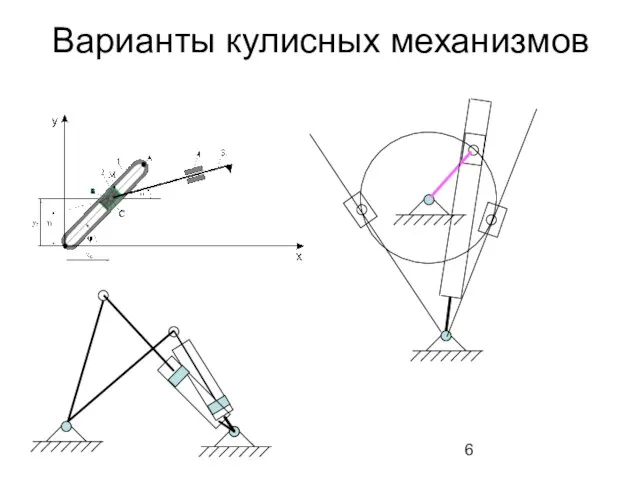
- 6. Варианты кулисных механизмов
- 7. Вращательное движение относительно неподвижной оси Р(a,b): Поступательное движение Sin(0)=0 Cos(0)=1 Переход от плоскопараллельного движения к вращательному
- 8. Координаты, компоненты скорости и ускорения для кривошипа Компоненты вектора ускорения О А Компоненты вектора скорости x
- 9. Координаты, компоненты скорости и ускорения для коромысла О А Компоненты вектора скорости Координаты Компоненты вектора ускорения
- 10. Координаты, компоненты скорости и ускорения для шатуна Уравнения движения в форме Лагранжа Компоненты скорости: в форме
- 11. Координаты, компоненты скорости и ускорения для ползуна Уравнения движения Компоненты вектора перемещения Компоненты вектора ускорения Компоненты
- 12. Кинематические связи в шарнирно - рычажных механизмах Кинематическими связями называют соотношения между постоянными (расстояния между осями
- 13. Кривошипно-ползунный механизм b b
- 14. Кривошипно-ползунный механизм (расчет через координаты точки А) А А b
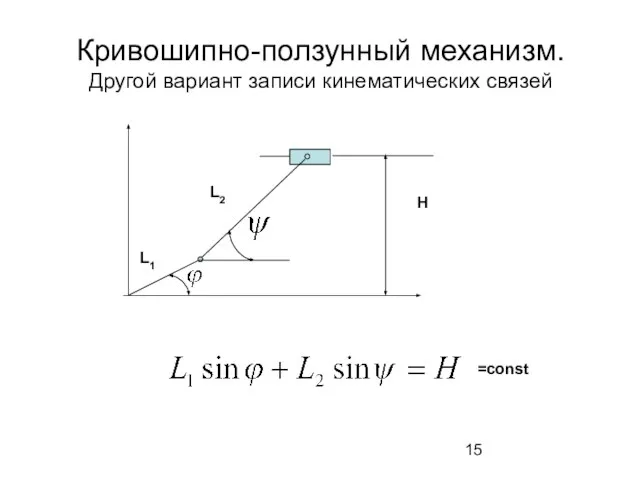
- 15. Кривошипно-ползунный механизм. Другой вариант записи кинематических связей Н L1 L2 =const
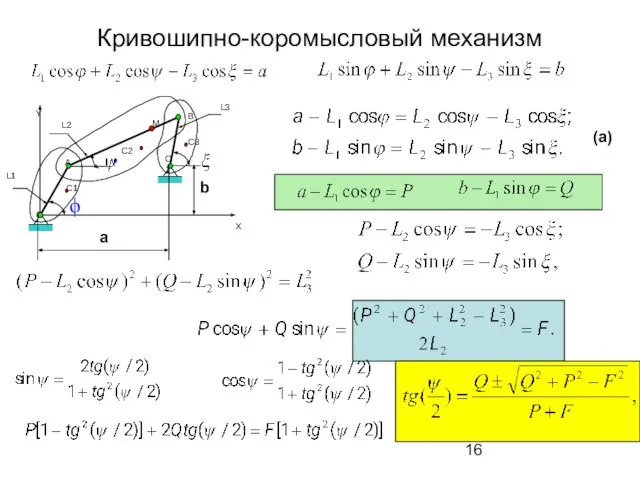
- 16. Кривошипно-коромысловый механизм O A B L2 L1 O1 C1 C2 M L3 X Y C3 ϕ
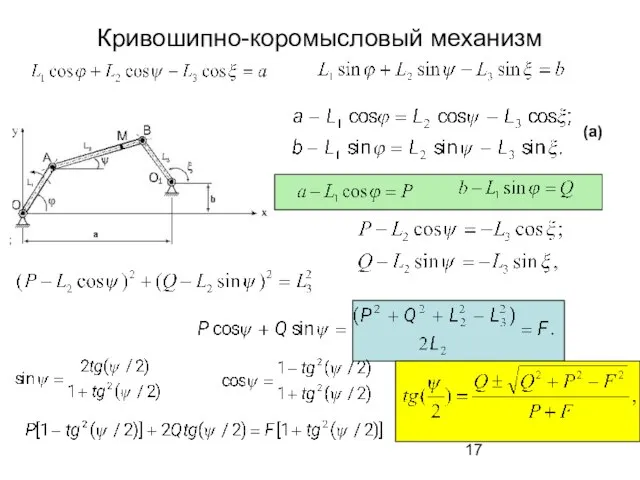
- 17. Кривошипно-коромысловый механизм ; (a)
- 18. Кривошипно-коромысловый механизм. Уравнения для углов наклона шатуна и коромысла ; (a) Из системы (а) получаем 4
- 19. Соотношения между угловыми скоростями для кривошипно-коромыслового механизма Дифференцируем систему уравнений (а) (см. сл. 16-18) по времени
- 20. Решение системы линейных уравнений по методу Крамера Исходная система и ее основной определитель «Дополнительные определители» Решение
- 21. Соотношения между угловыми ускорениями для кривошипно-коромыслового механизма Дифференцируем систему уравнений (b) (см. сл. 19) по времени
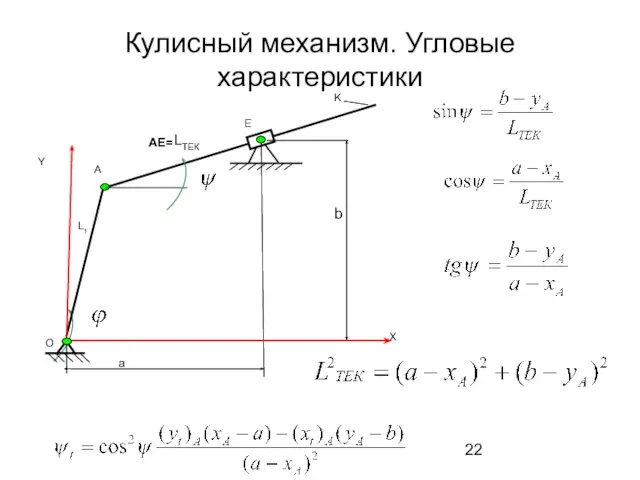
- 22. Кулисный механизм. Угловые характеристики AE=
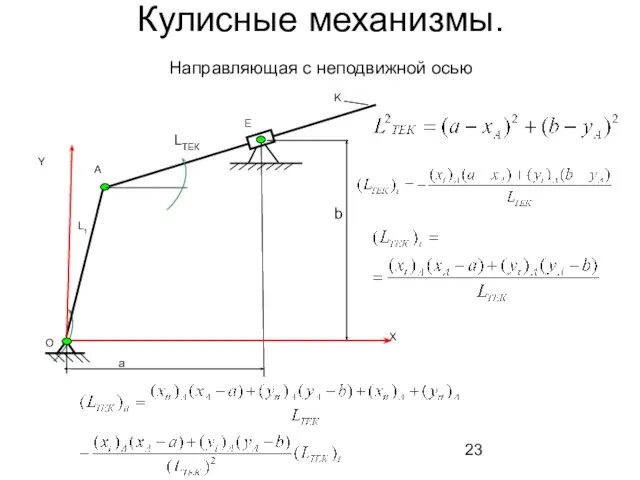
- 23. Кулисные механизмы. Направляющая с неподвижной осью
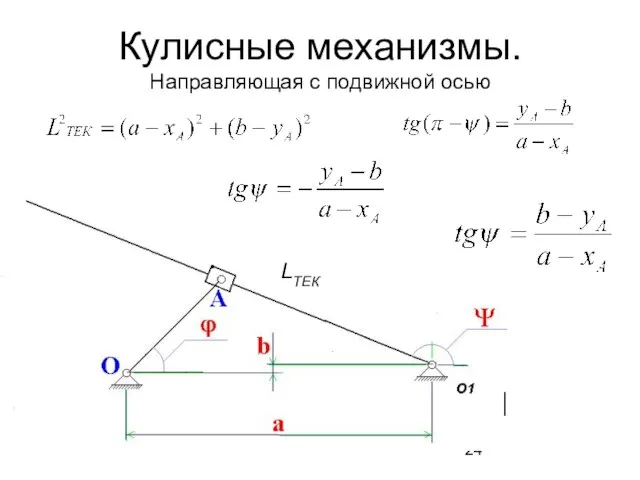
- 24. Кулисные механизмы. Направляющая с подвижной осью LТЕК
- 25. Все механизмы отличаются кинематическими связями. Число возможных вариантов механизмов и кинематических связей бесконечно.
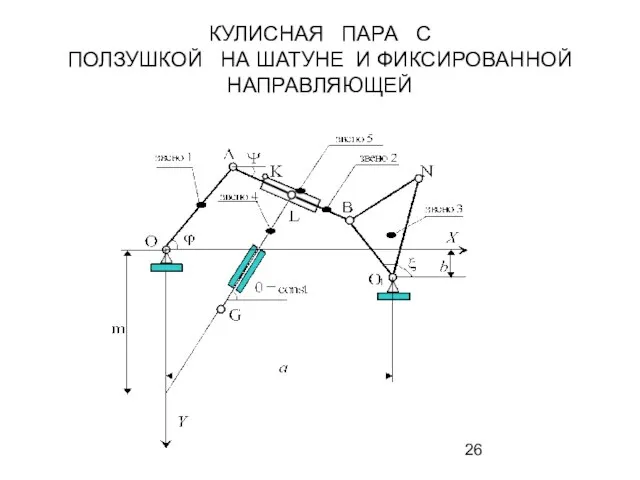
- 26. КУЛИСНАЯ ПАРА С ПОЛЗУШКОЙ НА ШАТУНЕ И ФИКСИРОВАННОЙ НАПРАВЛЯЮЩЕЙ
- 27. КУЛИСНАЯ ПАРА С ПОЛЗУШКОЙ НА ШАТУНЕ И ФИКСИРОВАННОЙ НАПРАВЛЯЮЩЕЙ Пусть уравнение фиксированной направляющей имеет вид (1)
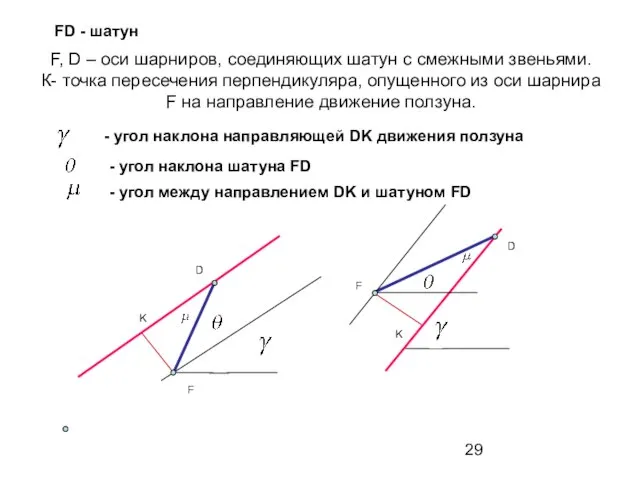
- 28. УГОЛ МЕЖДУ ШАТУНОМ И ФИКСИРОВАННЫМ НАПРАВЛЕНИЕМ ДВИЖЕНИЯ ПОЛЗУНА Уравнение прямой, вдоль которой движется ползун (1) где
- 29. F, D – оси шарниров, соединяющих шатун с смежными звеньями. К- точка пересечения перпендикуляра, опущенного из
- 30. Расстояние от точки Р(хР, уР) до прямой А*х + В*у + С = 0 определяет уравнение
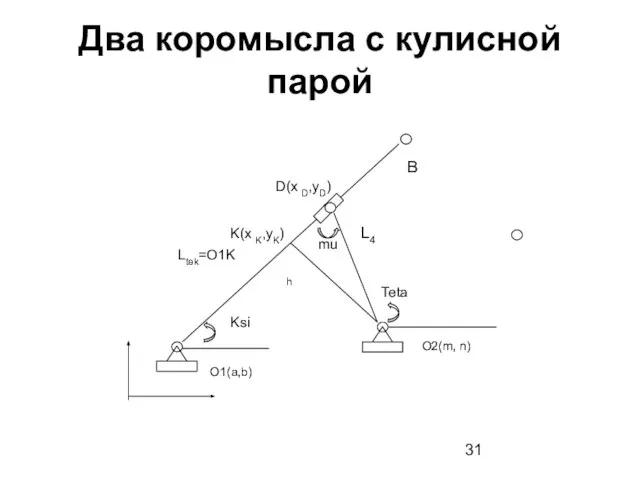
- 31. Два коромысла с кулисной парой
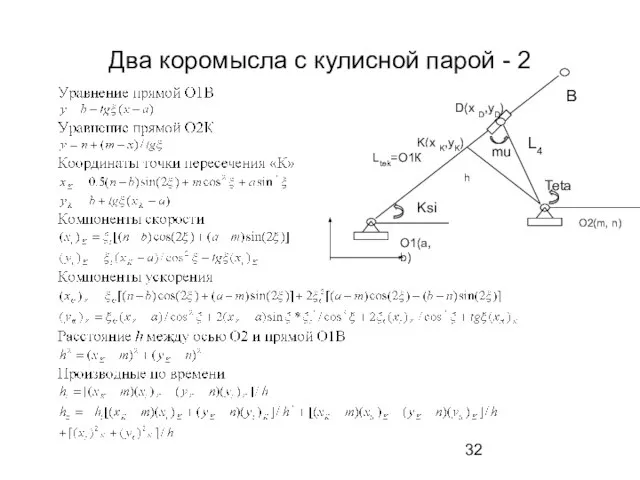
- 32. Два коромысла с кулисной парой - 2 D(x D,yD) K(x K,yK) O1(a,b) mu Teta Ksi L4
- 33. Два коромысла с кулисной парой - 3
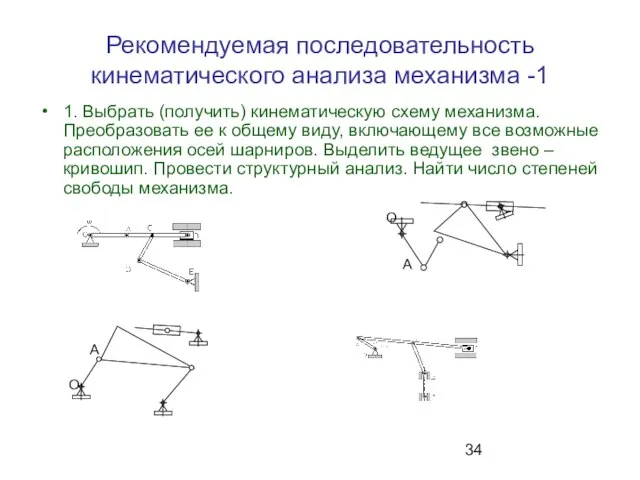
- 34. Рекомендуемая последовательность кинематического анализа механизма -1 1. Выбрать (получить) кинематическую схему механизма. Преобразовать ее к общему
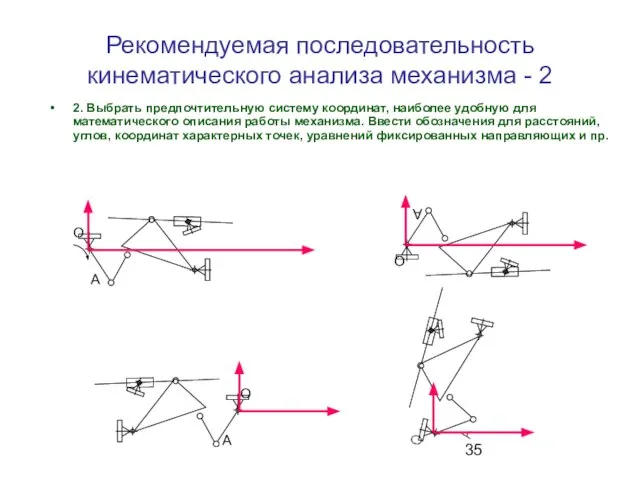
- 35. Рекомендуемая последовательность кинематического анализа механизма - 2 2. Выбрать предпочтительную систему координат, наиболее удобную для математического
- 36. Рекомендуемая последовательность кинематического анализа механизма-3 3. Для выбора допустимых соотношений расстояний между осями шарниров, обеспечивающих работоспособность
- 37. Рекомендуемая последовательность кинематического анализа механизма - 4 4. Выбрать основной («базовый») четырехзвенник механизма, включающий стойку и
- 38. Рекомендуемая последовательность кинематического анализа механизма - 5 5. Выписываем (из лекций или учебного пособия) уравнения для
- 39. Рекомендуемая последовательность кинематического анализа механизма - 6 6. Записываем уравнения кинематических связей для рассматриваемого четырехзвенника, находим
- 40. Рекомендуемая последовательность кинематического анализа механизма - 7 7. Переходим к программированию задачи, например в электронных таблицах
- 41. Рекомендуемая последовательность кинематического анализа механизма - 8 Переходим к программированию блока «Кинематические связи» 8.1. Вводим промежуточные
- 42. Рекомендуемая последовательность кинематического анализа механизма - 9 Переходим к программированию кинематических характеристик ведомых звеньев четырехзвенника 9.1.
- 43. Рекомендуемая последовательность кинематического анализа механизма - 10 Через каждые 5-8 строк программы проводим проверку результатов кинематических
- 45. Скачать презентацию





























 Рыба и рыбные продукты
Рыба и рыбные продукты NEFCO Целевые экологические программы
NEFCO Целевые экологические программы Основы законодательства РФ об охране здоровья гражданина
Основы законодательства РФ об охране здоровья гражданина 3.Essen und trinken
3.Essen und trinken Оценка эффективности проекта
Оценка эффективности проекта Анализ материалов
Анализ материалов Отчет по рекламе для студии воздушного фитнеса и йоги Притяжение за март 2019
Отчет по рекламе для студии воздушного фитнеса и йоги Притяжение за март 2019 Cистемная сорганизация бизнес-процессов
Cистемная сорганизация бизнес-процессов муниципальное бюджетное общеобразовательное учреждение "Начальная общеобразовательная школа № 41"
муниципальное бюджетное общеобразовательное учреждение "Начальная общеобразовательная школа № 41" Проектное бюро 3D плюс. Строительство зданий на основе визуализации в 3D формате объемнопланировочных решений
Проектное бюро 3D плюс. Строительство зданий на основе визуализации в 3D формате объемнопланировочных решений Внутреннее и внешнее устройство храма и правила поведения в храме
Внутреннее и внешнее устройство храма и правила поведения в храме Электроустановочные устройства квартиной электросети
Электроустановочные устройства квартиной электросети Рассказ А.И.Солженицына «Один день из жизни Ивана Денисовича»
Рассказ А.И.Солженицына «Один день из жизни Ивана Денисовича» Коза-заяц
Коза-заяц Виды кормов Ландор для кошек
Виды кормов Ландор для кошек Новая линейка мелкой бытовой техники Анна Фендрих Октябрь, 2 2009
Новая линейка мелкой бытовой техники Анна Фендрих Октябрь, 2 2009 Опорные схемы учебно – воспитательного курса «Основы религиозных культур и светской этики».
Опорные схемы учебно – воспитательного курса «Основы религиозных культур и светской этики».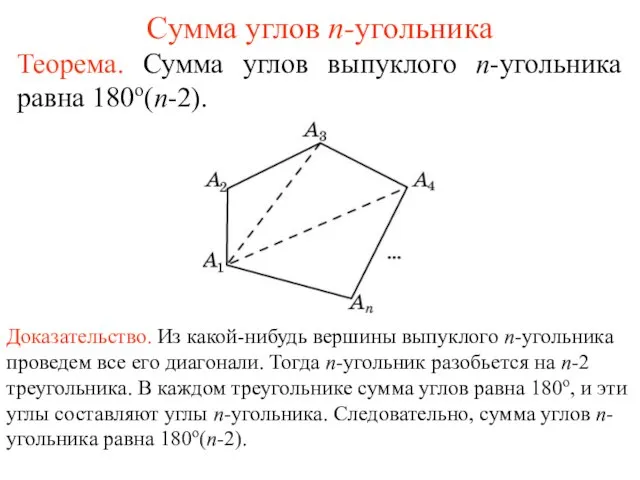 Сумма углов n-угольника
Сумма углов n-угольника Презентация группы компаний «НД»: «Автоматический платежный терминал для АЗС» «Холодная» АЗС в украинских реалиях: законодатель
Презентация группы компаний «НД»: «Автоматический платежный терминал для АЗС» «Холодная» АЗС в украинских реалиях: законодатель Ручная художественная вышивка
Ручная художественная вышивка УП «РЕКЛАМНАЯ КУХНЯ»
УП «РЕКЛАМНАЯ КУХНЯ» Презентация на тему Восклицательные предложения
Презентация на тему Восклицательные предложения Храмы России
Храмы России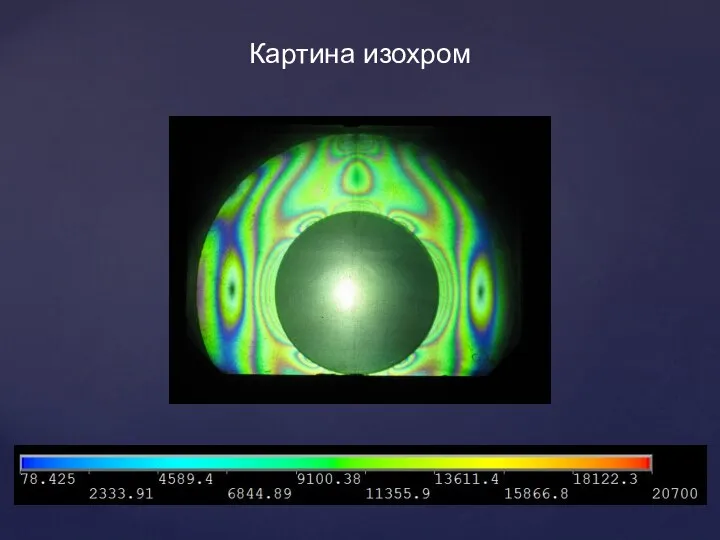 Картина изохром
Картина изохром Самый лучший спортсмен. Федор Чудинов
Самый лучший спортсмен. Федор Чудинов Игры к празднику Масленицы
Игры к празднику Масленицы Упражнения для мозга
Упражнения для мозга Последний император Николай II
Последний император Николай II