The second sign of equality of triangles

If the side and two adjoining angles of the same triangle are accordingly equal to the side and two adjoining angles of the other triangle, then these triangles are equal.

Given:
The triangle ABC and A1B1C1
AB is equal to A1B1
The angle A is equal to the angle A1
The angle B is equal to the angle B1
To be to prove that:
The triangle ABC is equal to the triangle A1B1C1

Proof
Let’s put the triangle ABC on the triangle A1B1C1 so that the apex A would be superposed with the apex A1, and the side AB would be superposed with equal side A1B1 and A1C1 and the apex C and C1 would be on the same side from the straight line A1B1.
As far as, the angle A is equal to the angle A1 and the angle B is equal to the angle B1, then the side AC will be put on the ray A1C1 and the side BC on the ray B1C1. So the apex C, which is the common point of the sides AC and AB, will be on both rays A1C1 and B1C1. Therefore, the apex C will be superposed with the common point of these rays, that is, the apex C1. That means the sides AC and A1C1, BC and B1C1 will be superposed.
As the triangle ABC and A1B1C1 are completely superposed, they are equal.
The theorem has been proved.

To proof the equality of the triangles LOC and NOM
Proof:
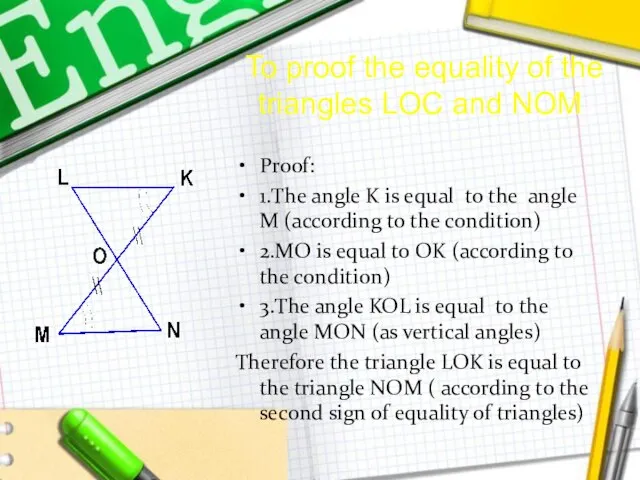
1.The angle K is equal to the angle M (according to the condition)
2.MO is equal to OK (according to the condition)
3.The angle KOL is equal to the angle MON (as vertical angles)
Therefore the triangle LOK is equal to the triangle NOM ( according to the second sign of equality of triangles)

The presentation has been done by:
Anna Zharkova, Maria Isakova, 7A form, school 511
L.I. Kunaeva, Maths teacher
V.V. Klyueva, English teacher
Moscow
2011