Содержание
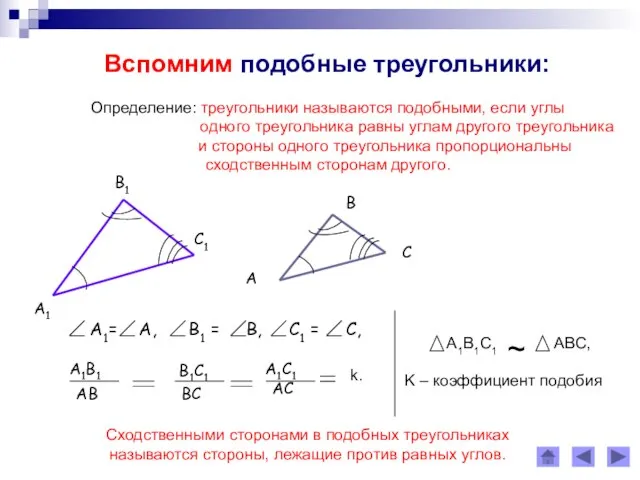
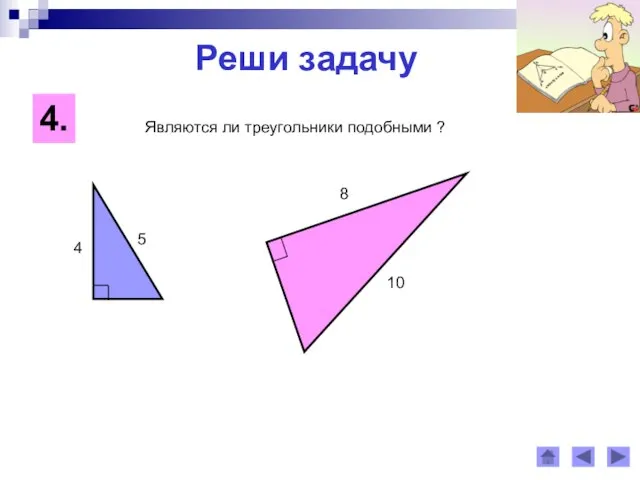
- 2. Вспомним подобные треугольники: Определение: треугольники называются подобными, если углы одного треугольника равны углам другого треугольника и
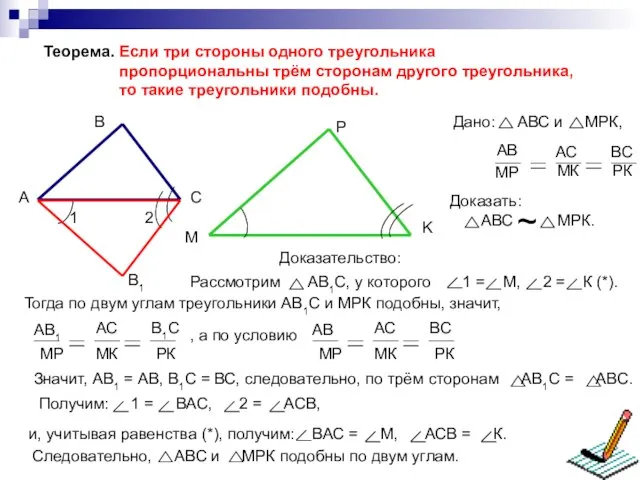
- 3. Теорема. Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны. Тогда
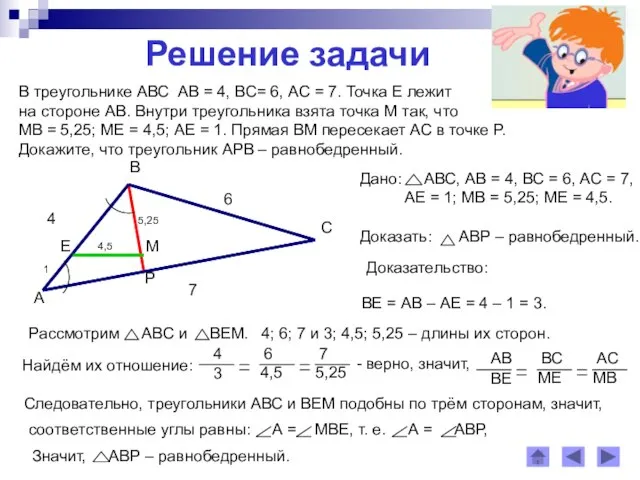
- 9. Решение задачи В треугольнике АВС АВ = 4, ВС= 6, АС = 7. Точка Е лежит
- 11. Скачать презентацию

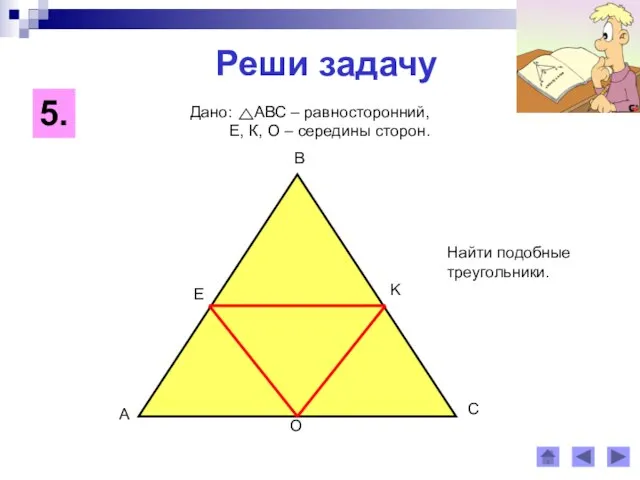
 Этапы формирования навыков
Этапы формирования навыков Торговая марка Мельница Семенова и Безбородова
Торговая марка Мельница Семенова и Безбородова Поддержка Электронного Правительства в Российской Федерации EuropeAid/126204/SER/RU Электронное правительство и услуги:пользователь – гр
Поддержка Электронного Правительства в Российской Федерации EuropeAid/126204/SER/RU Электронное правительство и услуги:пользователь – гр Древние святыни родного города
Древние святыни родного города Млечный путь
Млечный путь Принципы интервьюирования психосоматических пациентов
Принципы интервьюирования психосоматических пациентов Путешествие в неограниченную химию
Путешествие в неограниченную химию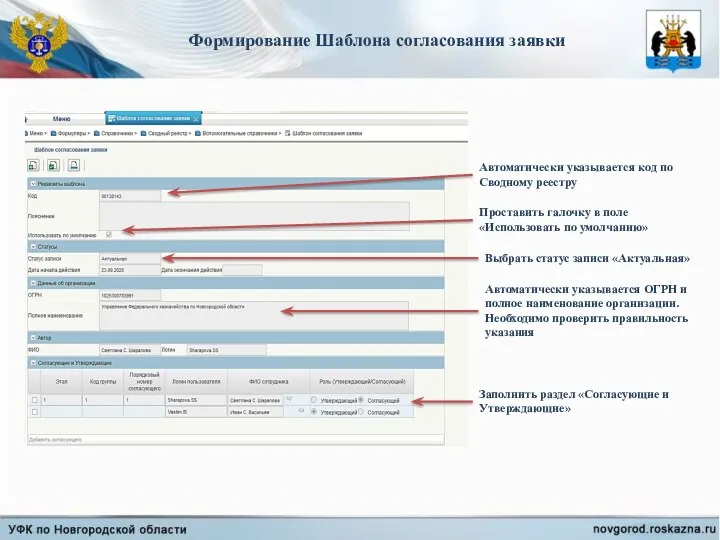 Шаблон согласования заявки в заявлении на изменение книги регистрации казначейских счетов
Шаблон согласования заявки в заявлении на изменение книги регистрации казначейских счетов Финансовое планирование жизни
Финансовое планирование жизни Презентация на тему СССР в период «перестройки»
Презентация на тему СССР в период «перестройки»  ddsda
ddsda Социализация учащихся в условиях компетентностного подхода к обучению
Социализация учащихся в условиях компетентностного подхода к обучению Олимпийские игры: символика ,история, география
Олимпийские игры: символика ,история, география Земли специального назначения
Земли специального назначения Сработанность и сплочённость коллектива
Сработанность и сплочённость коллектива Палеозойская эра
Палеозойская эра Перекрытия малоэтажных зданий
Перекрытия малоэтажных зданий Презентация на тему Тренинги для развития навыка быстрого чтения
Презентация на тему Тренинги для развития навыка быстрого чтения Математический закон красоты мира
Математический закон красоты мира Базовые правила покупок в интернете
Базовые правила покупок в интернете Кадомский вениз
Кадомский вениз Образ Бабы Яги – Хранительницы Входа в царство мёртвых
Образ Бабы Яги – Хранительницы Входа в царство мёртвых Исследование верхнего и нижнего течения реки Охта в Санкт-Петербурге.Начало исторического исследования.
Исследование верхнего и нижнего течения реки Охта в Санкт-Петербурге.Начало исторического исследования. ЗАО «ЭПИЭЛ»
ЗАО «ЭПИЭЛ» «Литературный клуб – основной системообразующий фактор классного сообщества»
«Литературный клуб – основной системообразующий фактор классного сообщества» Урок №23.
Урок №23. Презентация на тему Просвещение, устное народное творчество, литература в XIV- XVI веках
Презентация на тему Просвещение, устное народное творчество, литература в XIV- XVI веках Размещение продукта
Размещение продукта