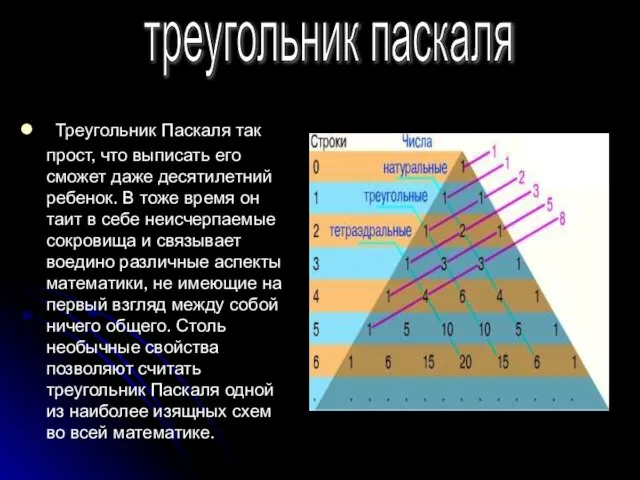
кружков можно расположить в виде треугольника - как классический пример начальная расстановка шаров в бильярде. К одной монетке можно прислонить еще две - итого три - к двум можно приладить еще три - итого шесть. Продолжая наращивать ряды с сохранением формы треугольника получим ряд 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66..., что и показывает вторая зеленая линия. Этот замечательный ряд, каждый член которого равен сумме натурального ряда чисел (55=1+2+3+4+5+6+7+8+9+10), содержит также множество знакомцев, хорошо известных любителям математики: 6 и 28 - совершенные числа, 36 - квадратное число, 8 и 21 - числа Фибоначчи. Следующая зеленая линия покажет нам тетраэдральные числа - один шар мы можем положить на три - итого четыре, под три подложим шесть - итого десять, и так далее.
треугольник паскаля







 Сервис Мечты
Сервис Мечты Основи формування і реєстраціi корисного сигналу в діапазоні
Основи формування і реєстраціi корисного сигналу в діапазоні Комплексная система автоматизации
Комплексная система автоматизации Телепорт
Телепорт Осторожно! Сосульки
Осторожно! Сосульки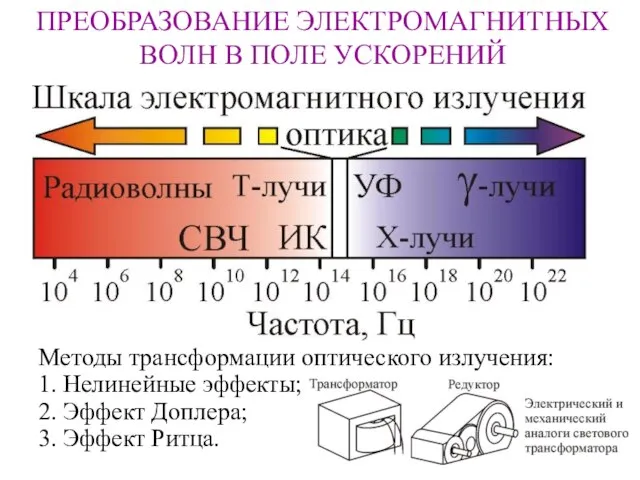 ПРЕОБРАЗОВАНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ПОЛЕ УСКОРЕНИЙ
ПРЕОБРАЗОВАНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ПОЛЕ УСКОРЕНИЙ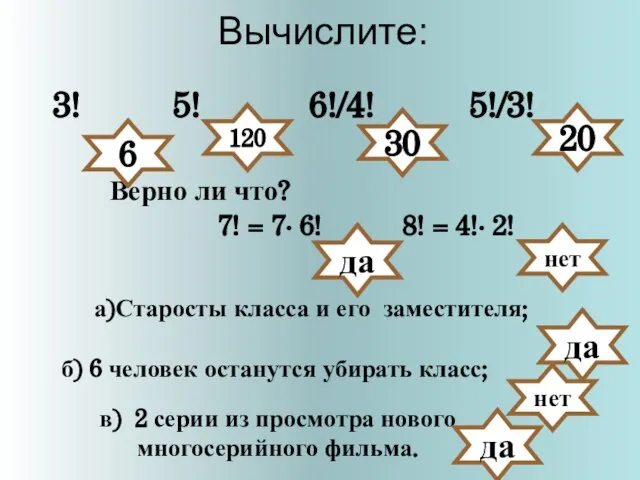 Примеры комбинаторных задач (9 класс)
Примеры комбинаторных задач (9 класс) Решение логических задач из курса кибернетики
Решение логических задач из курса кибернетики Бедность
Бедность Nocturnal eczema: Review of sleep and circadian rhythms
Nocturnal eczema: Review of sleep and circadian rhythms Microsoft Office Word 2007
Microsoft Office Word 2007 Международное сотрудничество в освоении космического пространства
Международное сотрудничество в освоении космического пространства Золото
Золото Презентация на тему Загадки о диких животных
Презентация на тему Загадки о диких животных Королева оркестра
Королева оркестра Экологическое просвещение в творчествеВладимира Алексеевича Чивилихина
Экологическое просвещение в творчествеВладимира Алексеевича Чивилихина Ҳозирги замон ҳуқуқи ва унинг моҳияти ҳақидаги концепциялар
Ҳозирги замон ҳуқуқи ва унинг моҳияти ҳақидаги концепциялар Образ Чичикова в поэме "Мертвые души"
Образ Чичикова в поэме "Мертвые души" Табір "Світанок"
Табір "Світанок" Презентация на тему Уфа – столица Башкортостана
Презентация на тему Уфа – столица Башкортостана Онтология
Онтология  Источники загрязнения окружающей среды
Источники загрязнения окружающей среды Project_A
Project_A Типы связи слов в словосочетании
Типы связи слов в словосочетании Всероссийский флешмоб Голубь мира
Всероссийский флешмоб Голубь мира Работа головного мозга находится в прямой зависимости от качества нашего питания, чем оно лучше, тем выше наши интеллектуальные во
Работа головного мозга находится в прямой зависимости от качества нашего питания, чем оно лучше, тем выше наши интеллектуальные во БИОСИНТЕЗ
БИОСИНТЕЗ Сусымалы компоненттерді мөлшерлеу мен қоспалау желісі. Дарис 12
Сусымалы компоненттерді мөлшерлеу мен қоспалау желісі. Дарис 12