Треугольникгеометрия 7 класс

План
Понятие треугольника.
Медианы, биссектрисы и высоты треугольника.
Классификация треугольников.
Первый признак равенства треугольников.
Второй признак равенства треугольников.
Третий признак равенства треугольников.
Тест .

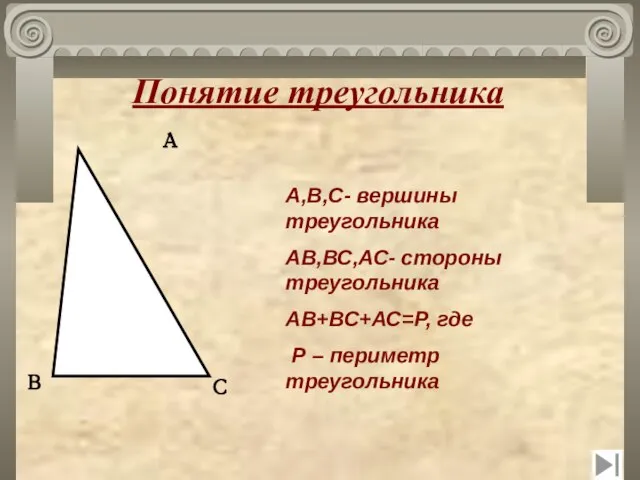
Понятие треугольника
А,В,С- вершины треугольника
АВ,ВС,АС- стороны треугольника
АВ+ВС+АС=Р, где
Р – периметр треугольника
А
С
В

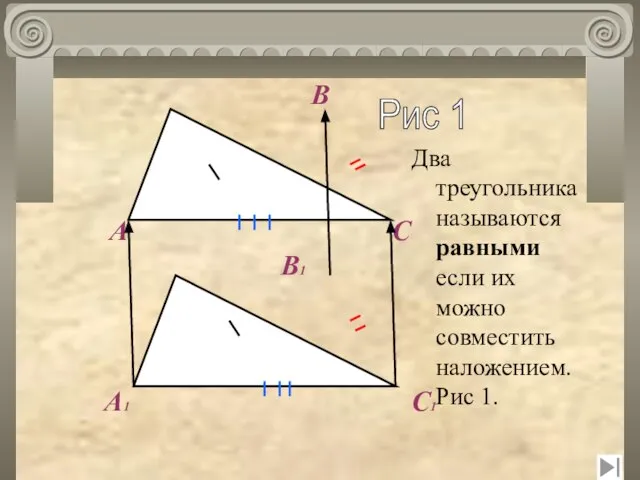
А
А1
В1
В
С
С1
Рис 1
Два треугольника называются равными если их можно совместить наложением. Рис 1.

Каждый из треугольников можно наложить на другой так, что они полностью совместятся, т.е попарно совместятся их вершины и стороны. Таким образом, если два треугольника равны, то элементы одного треугольника соответственно равны элементам другого треугольника.
В равных треугольниках против соответственно равных сторон лежат равные углы, и обратно: против соответственно равных углов лежат равные стороны.

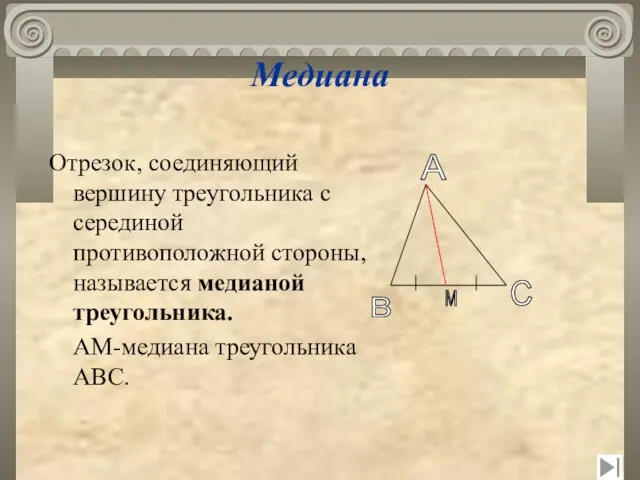
Медиана
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
АМ-медиана треугольника АВС.
A
M
B
C

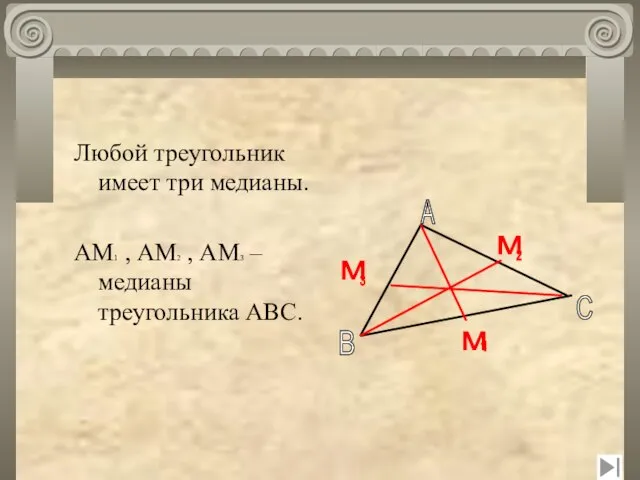
Любой треугольник имеет три медианы.
АМ1 , АМ2 , АМ3 –медианы треугольника АВС.
A
B
C
М
2
М
М
1
3

Биссектриса
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны,
называется биссектрисой угла треугольника.
АА1- биссектриса А треугольника АВС.
A
B
C
A
1

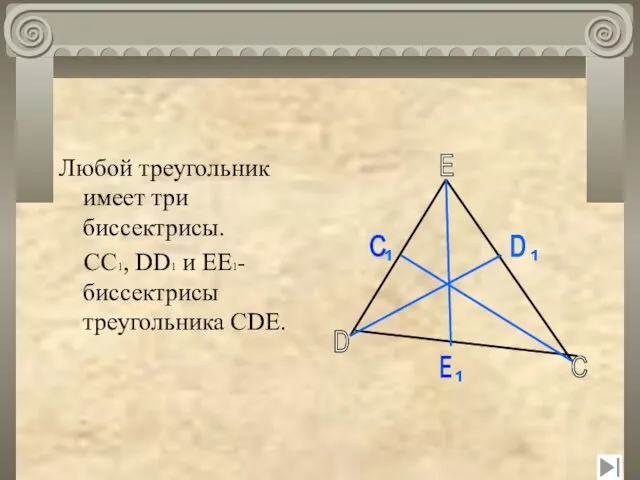
Любой треугольник имеет три биссектрисы.
CC1, DD1 и EE1- биссектрисы треугольника CDE.
D
E
C
C
E
D
1
1
1

Перпендикуляр, проведенный из вершины треугольника
к прямой, называется высотой треугольника.
АН-высота треугольника АВС
H
A
B
C Высота

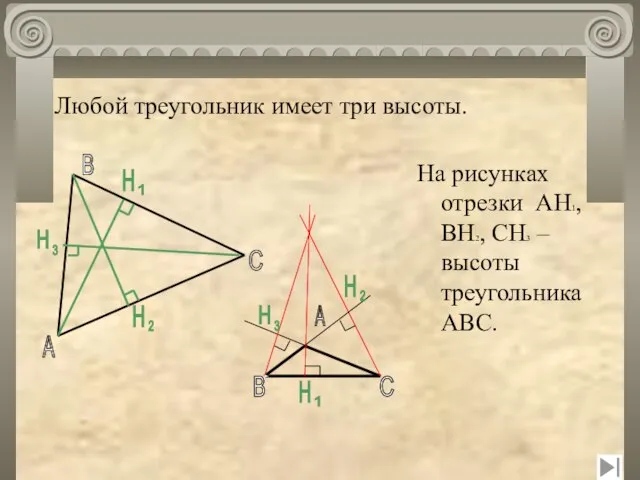
Любой треугольник имеет три высоты.
A
B
C
H
H
H
На рисунках отрезки AH1, BH2, CH3 – высоты треугольника ABC.
A
B
C
3
2
1
H
3
2
H
H
1

Медианы, биссектрисы и высоты треугольника обладают замечательными свойствами:
в любом треугольнике медианы пересекаются в одной точке; биссектрисы пересекаются в одной точке; высоты или их продолжения также пересекаются в одной точке

Классификация треугольников
По углам
тупоугольный
остроугольный
прямоугольный

Разносторонний
Треугольник называется разносторонним, если он имеет разные стороны и углы.
A
B
C
A≠ B ≠ C
AB=BC=CA

Равнобедренный
Треугольник называется равнобедренным,
если две его стороны равны. Равные стороны называются боковыми сторонами, а третья сторона – основанием равнобедренного треугольника.
Основание
Боковая
сторона
Боковая
сторона

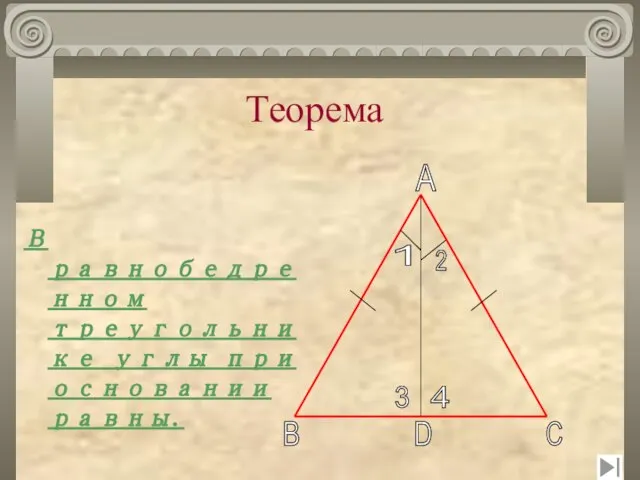
Теорема
В равнобедренном треугольнике углы при основании равны.
1
2
3
4
A
C
D
B

Рассмотрим равнобедренный треугольник ABC с основанием BC и докажем, что B= C. Пусть AD – биссектриса треугольника ABC . Треугольники ABD и ACD равны по первому признаку равенства треугольников (AB=AC по условию, AD – общая сторона, 1= 2, так как AD –биссектриса). В равных треугольниках против равных сторон лежат равные углы, поэтому B= C. Теорема доказана.
Доказательство:
1
2
3
4
A
C
D
B

Равносторонний
A
B
C
Треугольник, все стороны которого равны, называется равносторонним или правильным
AB=BC=CA
A≠ B ≠ C

Первый признак равенства треугольников
ТЕОРЕМА
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

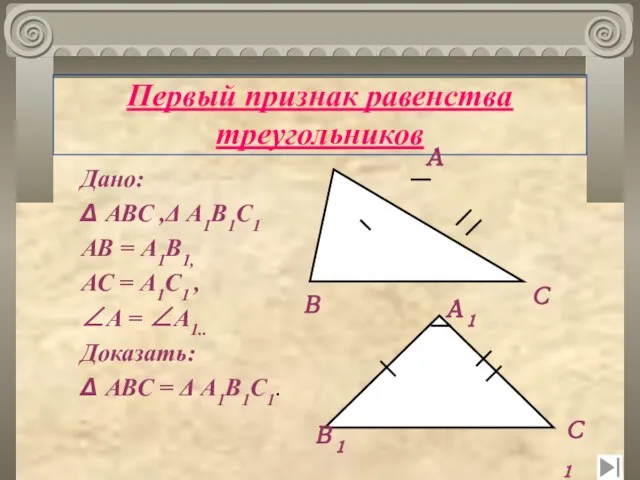
Первый признак равенства треугольников
Дано:
Δ АВС ,Δ А1В1С1
АВ = А1В1,
АС = А1С1 ,
∠А = ∠А1..
Доказать:
Δ АВС = Δ А1В1С1.
А
В
С
А1
В1
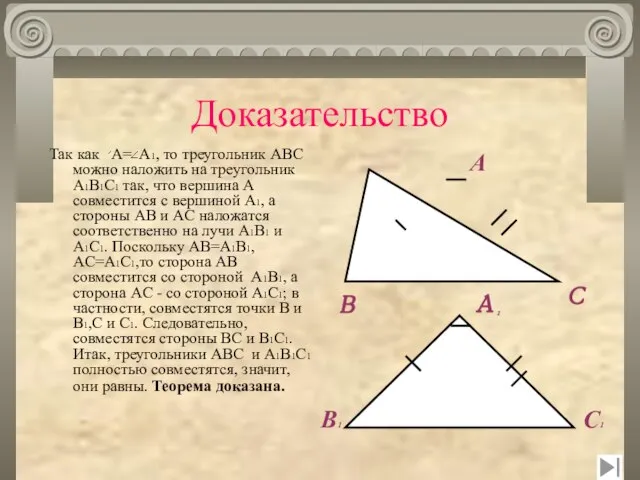
С1

Доказательство
Так как A= A1, то треугольник ABC можно наложить на треугольник A1B1C1 так, что вершина A совместится с вершиной A1, а стороны AB и AC наложатся соответственно на лучи A1B1 и A1C1. Поскольку AB=A1B1, AC=A1C1,то сторона AB совместится со стороной A1B1, а сторона AC - со стороной A1C1; в частности, совместятся точки B и B1,C и C1. Следовательно, совместятся стороны BC и B1C1. Итак, треугольники ABC и A1B1C1 полностью совместятся, значит, они равны. Теорема доказана.
В
С
А1
А
В1
С1

Второй признак равенства треугольников
ТЕОРЕМА
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны

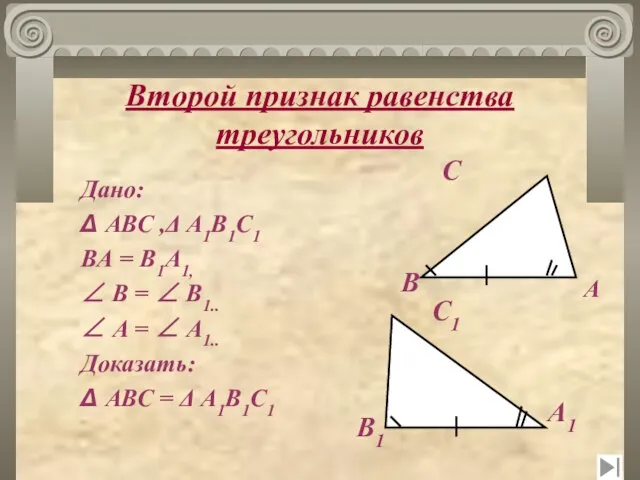
Второй признак равенства треугольников
Дано:
Δ АВС ,Δ А1В1С1
ВА = В1А1,
∠ В = ∠ В1..
∠ А = ∠ А1..
Доказать:
Δ АВС = Δ А1В1С1
А1
В
А
В1
С
С1

Доказательство
Наложим треугольник ABC на A 1B1C 1 так, чтобы вершина A совместилась с вершиной A 1, сторона AB – c равной ей стороной A 1 B 1, а вершины C и C1 оказались по одну сторону от прямой A 1 B 1. Так как A= A 1 и B= B 1, то сторона AC наложится на луч A1C 1, а сторона BC – на луч B 1 C 1. Поэтому вершина C – общая точка сторон AC и BC – окажется лежащей как на луче A 1 C 1, так и на луче B 1 C 1 и, следовательно, совместится с общей точкой этих лучей – вершиной C 1. Значит, совместятся стороны AC и A 1 C 1, BC и B 1 C 1. Итак, треугольники ABC и A 1B1C 1 полностью совместятся, поэтому они равны. Теорема доказана.
В
А
В1
С1
С
А1

Третий признак равенства треугольников
ТЕОРЕМА
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

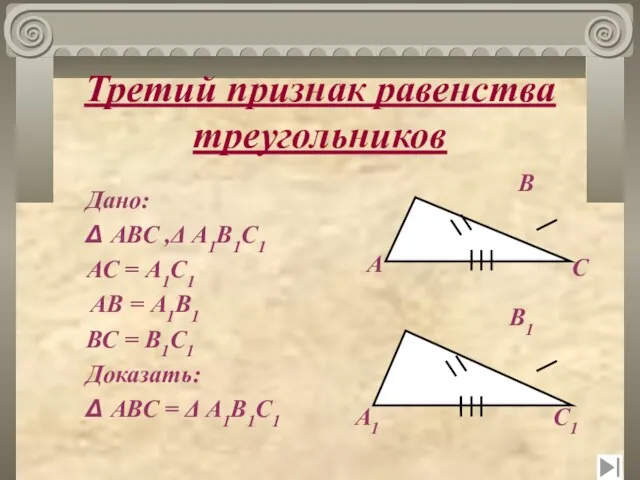
Третий признак равенства треугольников
Дано:
Δ АВС ,Δ А1В1С1
АС = А1С1
АВ = А1В1
ВС = В1С1
Доказать:
Δ АВС = Δ А1В1С1
А
В
С
А1
В1
С1

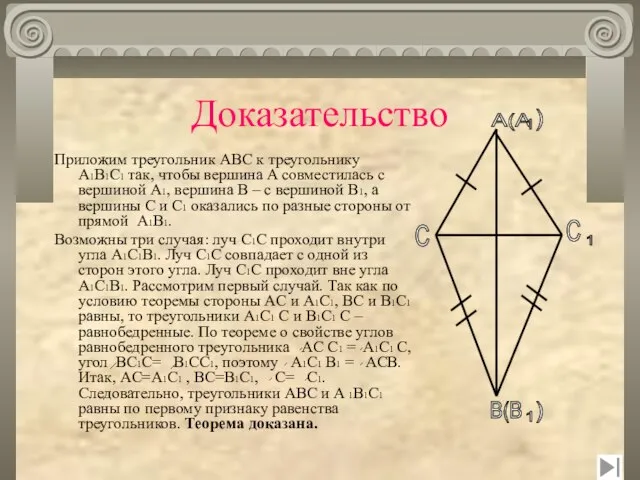
Доказательство
Приложим треугольник ABC к треугольнику A1B1C1 так, чтобы вершина A совместилась с вершиной A1, вершина B – с вершиной B1, а вершины C и C1 оказались по разные стороны от прямой A1B1.
Возможны три случая: луч C1C проходит внутри угла A1C1B1. Луч C1C совпадает с одной из сторон этого угла. Луч C1C проходит вне угла A1C1B1. Рассмотрим первый случай. Так как по условию теоремы стороны AC и A1C1, BC и B1C1 равны, то треугольники A1C1 C и B1C1 C – равнобедренные. По теореме о свойстве углов равнобедренного треугольника AС C1 = A1C1 С, угол BС1С= B1СС1, поэтому A1C1 B1 = ACB. Итак, AC=A1C1 , BC=B1C1, C= C1. Следовательно, треугольники ABC и A 1B1C1 равны по первому признаку равенства треугольников. Теорема доказана.
A(A
1
)
C
C
1
В(В
1
)

Тест.
1.Для доказательства равенства треугольников
АВС и DEF(рис1) достаточно знать, что:
а) АВ=DF; б)АС=DE; в)АВ=DE.
2.Для доказательства равенства треугольников АВС и EDF(рис 2) достаточно доказать, что:
а) А= D б) В= D в) А= Е .
3.Из равенства треугольников АВС и FDE(рис 3)следует, что:
а)АВ=FD б)АС=DF в)АВ=EF .
4.Из равенства треугольников АВС и DEF(рис 4) следует, что:
а) В= D б) А= Е в) С= F .
A
B
C
D
E
F
B
C
A
E
E
E
D
D
D
F
F
F
A
A
B
B
C
C
рис.1
рис.2
рис.4
рис.3

5.В треугольнике АВС все стороны равны, и в треугольнике DEF все стороны равны. Чтобы доказать равенство треугольников АВС и DEF достаточно доказать, что :
а) В= D; б)АВ=DE; в)РАВС=РDEF .
6. «Медиана в равнобедренном треугольнике является биссектрисой и высотой».Это утверждение :
а)верно всегда; б)всегда неверно; в)может быть верно.
7.В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
а)в любом; б)в равнобедренном; в)в равностороннем.
8.Если в треугольнике два угла равны, то этот треугольник:
а)равнобедренный; б)равносторонний; в)прямоугольный.
9.Если треугольник равносторонний, то:
а)он равнобедренный; б)все его углы равны;
в) любая его биссектриса является медианой и высотой.