Треугольник, простейший и неисчерпаемый. Задачи для подготовки к ЕГЭ.

Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение.
В. Произволов

Аннотация к работе.
Цель нашей работы - помочь учащимся подготовиться к итоговой аттестации. Для успешного выполнения экзаменационных заданий необходимы твердые знания основных геометрических фактов и некоторый практический опыт .
Работа может быть полезна учащимся не только 9 класса, но и 8 и 10 классов, которые в будущем будут сдавать ЕГЭ.
Кроме того, надеемся , что наша презентация послужит хорошим подспорьем для учителей математики при проведении уроков по темам , связанным с треугольником.
Текст на слайдах появляется по щелчку мышки, есть время подумать над задачей , проанализировать условие, потом сравнить свое решение с нашим.
Презентация содержит историческую справку о треугольниках и краткий справочный материал.

Задача №1
Задача №2
Задача №3
Задача №4
Задача №5
Задача №6
Задача №7
Задача №8
Задача №9
Содержание .
Исторические сведения
Справочный материал

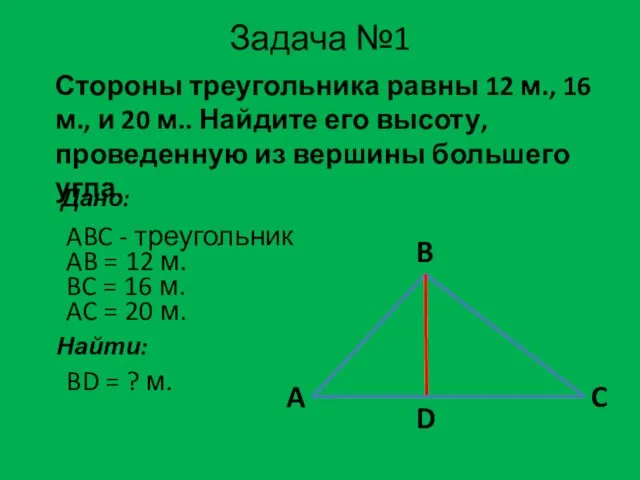
Задача №1
Стороны треугольника равны 12 м., 16 м., и 20 м.. Найдите его высоту, проведенную из вершины большего угла.
Дано:
A
B
C
ABC - треугольник
AB = 12 м.
BC = 16 м.
AC = 20 м.
Найти:
BD = ? м.
D

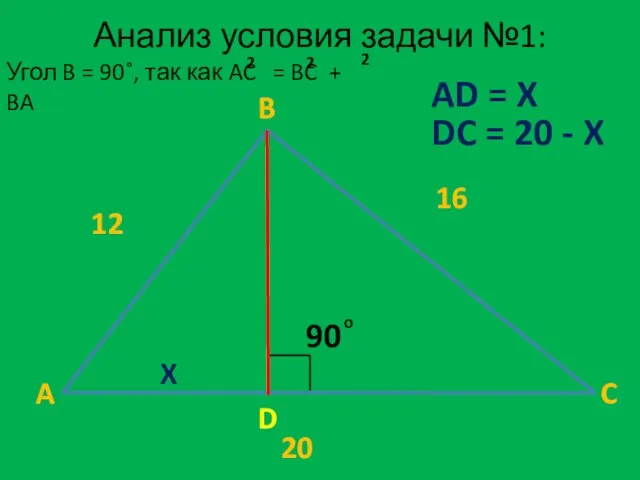
Анализ условия задачи №1:
A
B
C
D
12
16
20
X
AD = X
DC = 20 - X

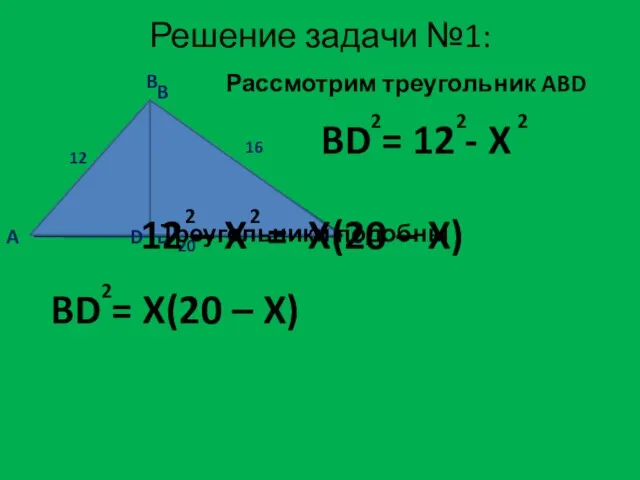
Решение задачи №1:
A
B
D
Рассмотрим треугольник ABD
C
B
Треугольники подобны

144 – 20X = 0
7,5 – X = 0
X = 7,2
BD = 9,6
Решение задачи №1:

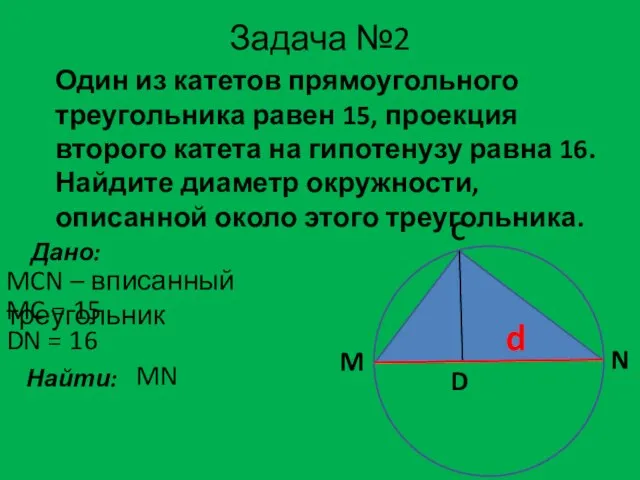
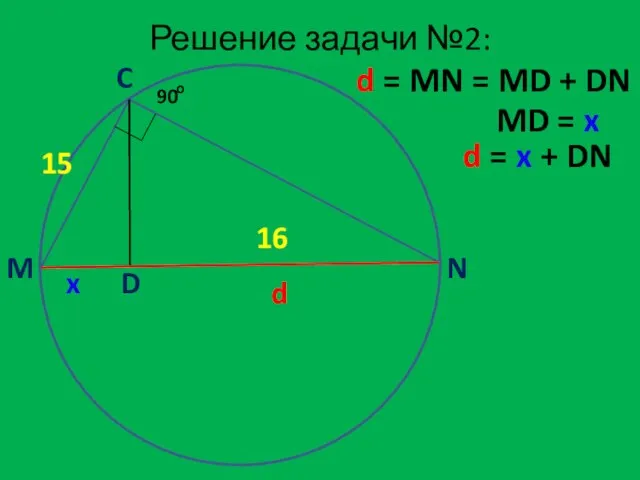
Задача №2
Один из катетов прямоугольного треугольника равен 15, проекция второго катета на гипотенузу равна 16. Найдите диаметр окружности, описанной около этого треугольника.
Дано:
MCN – вписанный треугольник
MC = 15
Найти:
MN
M
C
N
D
DN = 16
d

Решение задачи №2:
M
C
N
D
15
16
d
d = MN = MD + DN
MD = x
x
d = x + DN

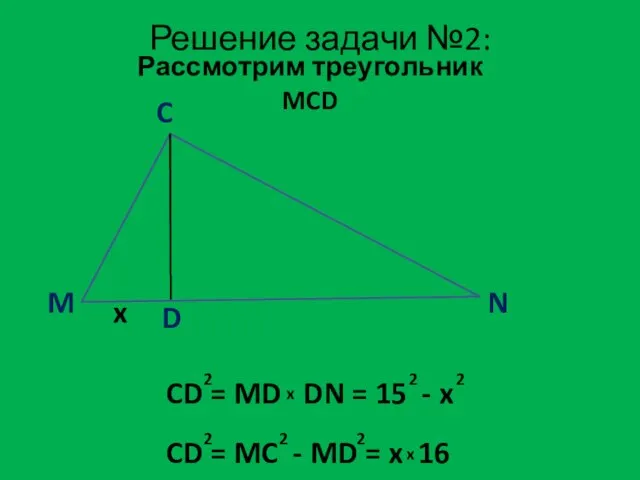
M
C
N
D
x
Решение задачи №2:
Рассмотрим треугольник MCD

Решение задачи №2:
D = 256 + 900 = 1156
d = x + DN
d = 9 + 16 = 25

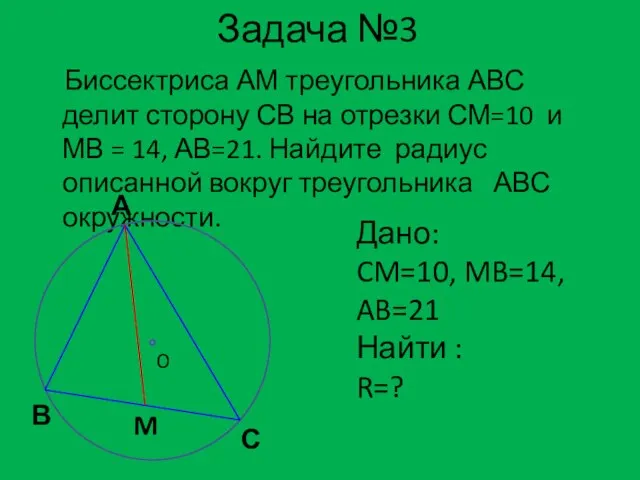
Задача №3
Биссектриса АМ треугольника АВС делит сторону СВ на отрезки СМ=10 и МВ = 14, АВ=21. Найдите радиус описанной вокруг треугольника АВС окружности.
Дано:
CM=10, MB=14,
AB=21
Найти :
R=?

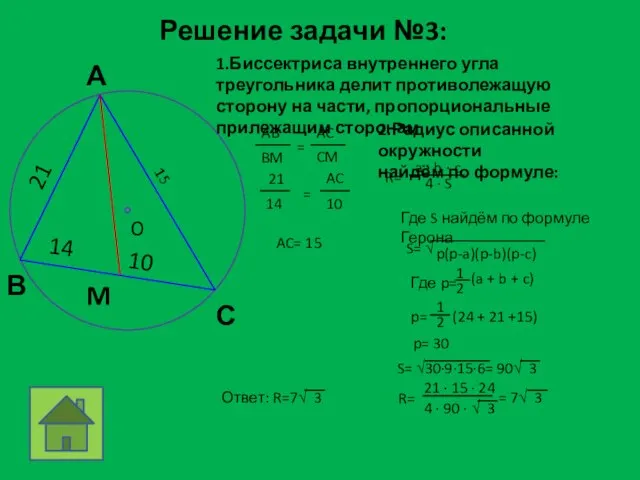
Решение задачи №3:
M
14
10
21
1.Биссектриса внутреннего угла треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам.
AC= 15
15
p= 30

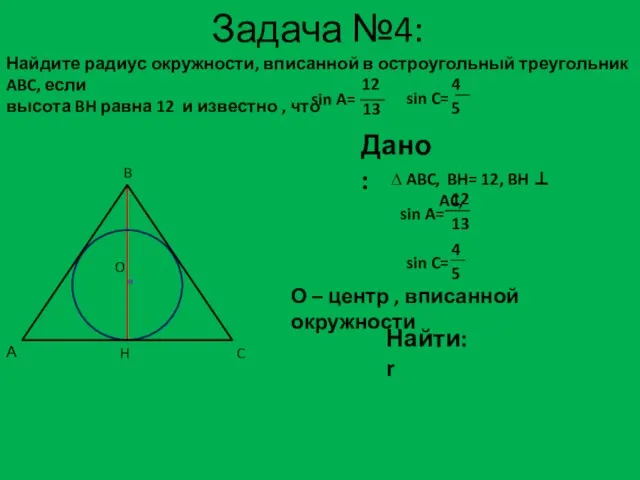
Задача №4:
Дано:
∆ ABC,
H
BH= 12, BH ⊥ AC,
Найти: r
Найдите радиус окружности, вписанной в остроугольный треугольник ABC, если
высота BH равна 12 и известно , что
О – центр , вписанной окружности

Решение задачи №4:
4. HC² = BC² - BH² = 225 – 144 = 81
HC = 9
5. AH² = AB² - BH² = 25
AH = 5
6. AC = AH + HC = 14
21
Ответ : r = 4

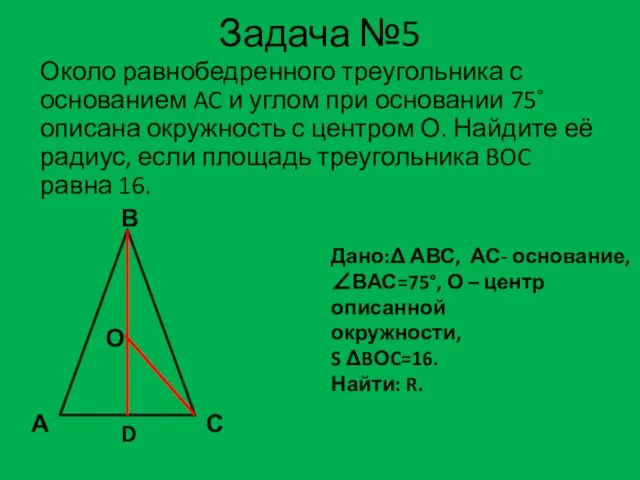
Задача №5
Около равнобедренного треугольника с основанием AC и углом при основании 75˚ описана окружность с центром О. Найдите её радиус, если площадь треугольника BOC равна 16.
Дано:Δ АВС, АС- основание,
∠ВАС=75°, О – центр описанной
окружности,
S ΔBОC=16.
Найти: R.

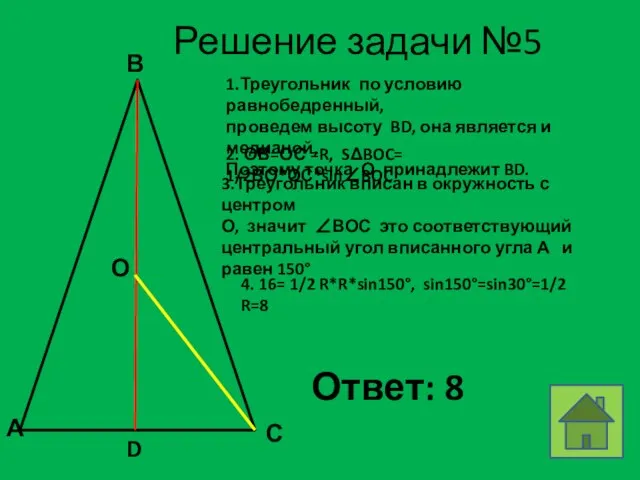
Решение задачи №5
В
А
С
О
D
1.Треугольник по условию равнобедренный,
проведем высоту BD, она является и медианой,
Поэтому точка О принадлежит BD.
2. ОВ=ОС =R, SΔBOC= 1/2ВО*ОС*sin∠BOC
3.Треугольник вписан в окружность с центром
О, значит ∠ВОС это соответствующий
центральный угол вписанного угла А и
равен 150°
4. 16= 1/2 R*R*sin150°, sin150°=sin30°=1/2
R=8
Ответ: 8

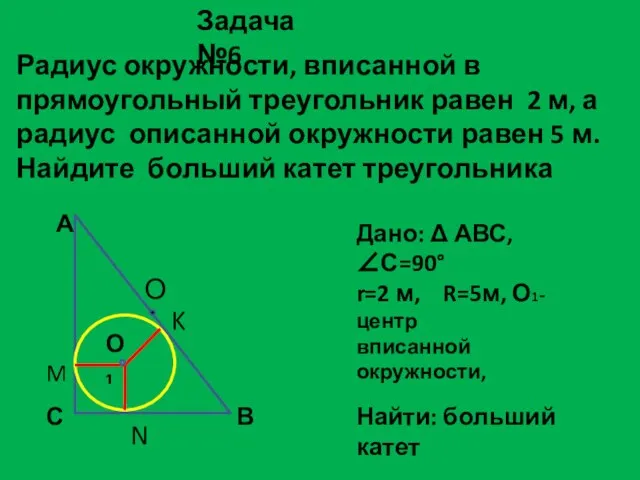
Радиус окружности, вписанной в прямоугольный треугольник равен 2 м, а радиус описанной окружности равен 5 м.
Найдите больший катет треугольника
Задача №6
Дано: Δ АВС, ∠С=90°
r=2 м, R=5м, О1- центр
вписанной окружности,
Найти: больший катет

Решение задачи №6
О – центр описанной окружности; так как треугольник АСВ
прямоугольный, то его гипотенуза является диаметром
окружности, угол АСB =90° и является вписанным
AB = 2R = 5 ∙ 2 = 10 м.
3. Отрезки BK и BN равны как отрезки касательных,
проведенных из одной точки,
аналогично CN = CM;
AM = AK; обозначим BK = BN = x; тогда CB = 2 + x;
AK = AM = 10 – x; AC = 12 – x.
4. По т. Пифагора AB² = CB² + AC²; 10² = (2 + x)² + (12 –x)²
2x² - 20x + 48 = 0, x² - 10x = 24 = 0,
x₁ = 6, x₂ = 4;
AC = 12- 6 = 6; CB = 2 + 6 = 8м.
Ответ: 8м.

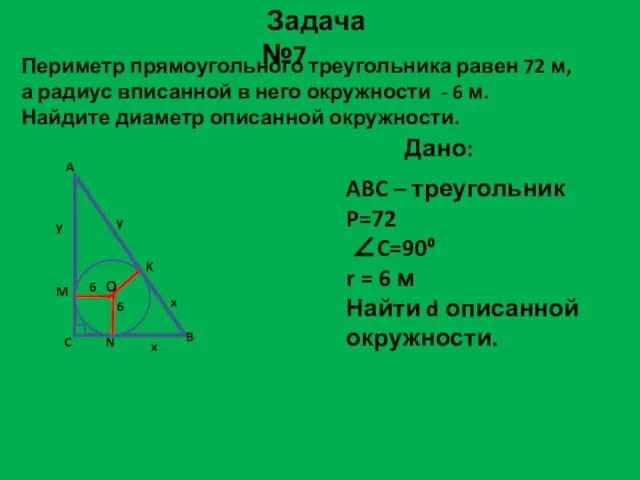
Периметр прямоугольного треугольника равен 72 м, а радиус вписанной в него окружности - 6 м.
Найдите диаметр описанной окружности.
Дано:
ABC – треугольник
P=72
∠C=90⁰
r = 6 м
Найти d описанной окружности.
Задача №7

Решение задачи №7:
∆АВС – прямоугольный ; угол C = 90˚,
Значит диаметр описанной окружности совпадает с
гипотенузой т.е. d=AB
3. Обозначим отрезки BN = BK = x (OK ⊥ AB)
OK=r , ВN=ВК как отрезки касательных AM = MK = y
P ∆АВС = AC + AB + CB, но
АС = 6+у, АВ = x + у СВ = 6+х
P ∆АВС = 6+у+х+у+6+х = 12+2х+2у = 72 (по условию)
х + у = (72-12) : 2 , х + у = 30 , АВ=30
Ответ : 30

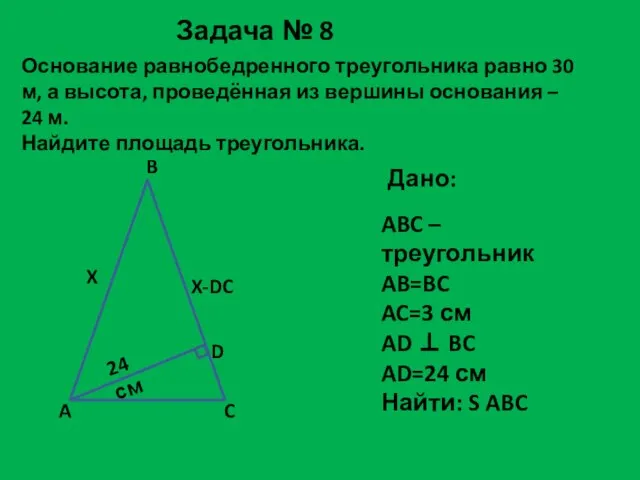
Основание равнобедренного треугольника равно 30 м, а высота, проведённая из вершины основания – 24 м.
Найдите площадь треугольника.
Дано:
ABC – треугольник
AB=BC
AC=3 см
AD ⊥ BC
AD=24 см
Найти: S ABC
Задача № 8

Решение задачи №8:
S ∆АВС = ½ AD ∙ BC
Найдём ВС, обозначим АВ = ВС = х, тогда DB = x - DC
2. Из ∆АВС найдём DC
DB = x -18

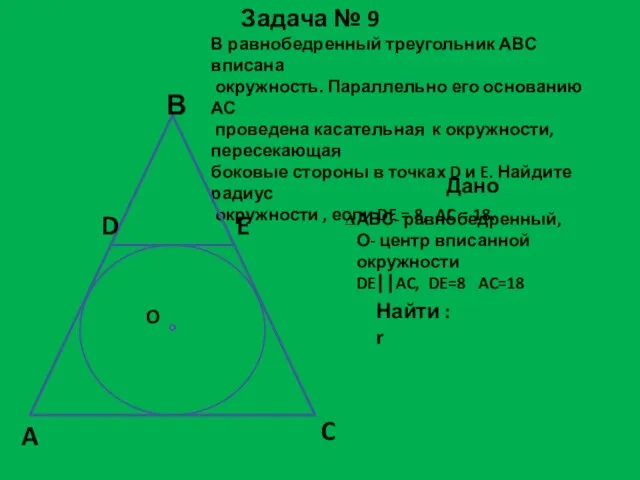
Задача № 9
В равнобедренный треугольник АВС вписана
окружность. Параллельно его основанию АС проведена касательная к окружности, пересекающая
боковые стороны в точках D и E. Найдите радиус
окружности , если DE = 8, AC = 18.
Дано:
АВС- равнобедренный,
О- центр вписанной окружности
DE⎮⎮AC, DE=8 AC=18
В
D
E
A
C
Найти : r
O

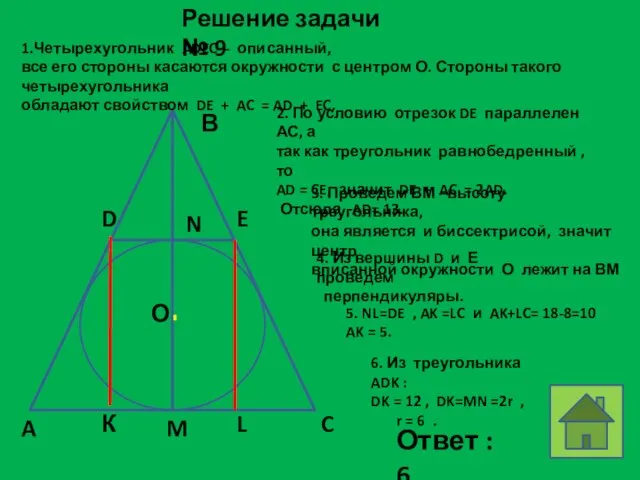
О
В
D
N
E
M
A
C
Решение задачи № 9
1.Четырехугольник ADEC - описанный,
все его стороны касаются окружности с центром О. Стороны такого четырехугольника
обладают свойством DE + AC = AD + EC.
2. По условию отрезок DE параллелен АС, а
так как треугольник равнобедренный , то
AD = CE, значит DE + AC = 2AD.
Отсюда AD= 13.
3. Проведем ВМ –высоту треугольника,
она является и биссектрисой, значит центр
вписанной окружности О лежит на ВМ
4. Из вершины D и Е проведем
перпендикуляры.
К
L
6. Из треугольника ADK :
DK = 12 , DK=MN =2r ,
r = 6 .
5. NL=DE , AK =LC и AK+LC= 18-8=10
AK = 5.
Ответ : 6.

Исторические сведения.
Треугольник - самая простая замкнутая прямолинейная фигура; одна из первых, свойства которой человек узнал еще в глубокой древности, так как эта фигура всегда имела широкое применение в практической жизни. В строительном искусстве испокон веков используется свойство жесткости треугольника для укрепления различных строений и их деталей. Изображения треугольников и задачи на треугольники встречаются в папирусах, в старинных индийских книгах и в других древних документах. В древней Греции учение о треугольниках развивалось в ионийской школе, основанной в VII в. до н. э. Фалесом, в школе Пифагора и других; оно было затем полностью изложено в первой книге «Начал» Евклида. Понятие о треугольнике исторически развивалось, так: сначала рассматривались лишь правильные, затем равнобедренные и, наконец, разносторонние треугольники.
Фалес Пифагор
640/624 до н. э. прим. 570 до н. э.
Евклид II век до н. э.

Справочный материал
Проекция катета на гипотенузу- отрезок (часть гипотенузы) , соединяющий
основание перпендикуляра , опущенного из прямого угла
и конец катета, общий с гипотенузой.
Окружность, касающаяся всех трех сторон треугольника, называется его
вписанной окружностью
. Окружность, проходящая через все три вершины треугольника, называется его
описанной окружностью.
Биссектрисой треугольника, проведенной из данной вершины, называют
отрезок, соединяющий эту вершину с точкой на противоположной стороне и
делящий угол при данной вершине пополам.
Биссектрисы треугольника пересекаются в одной точке, и эта точка совпадает с центром вписанной окружности.
В равнобедренном треугольнике биссектриса, медиана и высота, проведенные
к основанию, совпадают.
Серединные перпендикуляры к сторонам треугольника пересекаются в одной
точке, которая совпадает с центром описанной окружности.